Файл: Методические указания к выполнению самостоятельной работы для бакалавров 15. 03. 04 Автоматизация технологических процессов и производств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 158
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
где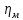 – механический к.п.д. гидропривода, равный произведению механических к.п.д. насоса и гидродвигателя ;
– механический к.п.д. гидропривода, равный произведению механических к.п.д. насоса и гидродвигателя ; 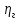 – гидравлический к.п.д., равный отношению потерь давления в гидролиниях к давлению на выходе из насоса.
– гидравлический к.п.д., равный отношению потерь давления в гидролиниях к давлению на выходе из насоса. 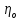 − объёмный к.п.д. гидропривода.
− объёмный к.п.д. гидропривода.
К.п.д. гидропривода с дроссельным управлением помимо перечисленных потерь учитывает и к.п.д. системы управления , который равен отношению мощности потока жидкости , подведённого к гидродвигателю, к мощности потока жидкости на выходе из насоса без учёта потерь в гидролиниях.
При последовательном включении дросселя
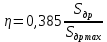 ,
,
при параллельном включении дросселя
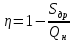 ,
,
здесь Sдр и Sдр max − соответственно текущая и максимальная величина площади проходного сечения дросселя; Qдр − расход через дроссель.
Гидроприводы при расчётах можно рассматривать как сложные трубопроводы с насосной подачей,, а гидродвигатели − как особые местные сопротивления , вызывающие потерю давления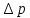 . Эта величина считается независящей от расхода жидкости (скорости перемещения выходного звена поршня) . Для гидроцилиндров величина
. Эта величина считается независящей от расхода жидкости (скорости перемещения выходного звена поршня) . Для гидроцилиндров величина 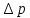 приближённо определяется как частное от деления нагрузки вдоль штока на площадь поршня со стороны нагнетания При расчёте указанных схем следует учитывать то, что расход жидкости на входе в гидроцилиндр с односторонним штоком отличен от расхода на выходе, так как площади поршня различны.
приближённо определяется как частное от деления нагрузки вдоль штока на площадь поршня со стороны нагнетания При расчёте указанных схем следует учитывать то, что расход жидкости на входе в гидроцилиндр с односторонним штоком отличен от расхода на выходе, так как площади поршня различны.
В основе расчёта трубопроводов лежат формула Дарси ,для определения потерь напора на трение по длине потока и формула Вейсбаха для расчёта местных потерь.
При ламинарном режиме ( Re < 2300) удобнее пользоваться формулой Пуазейля
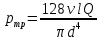 ,
,
где pтр – потеря давления на трение в трубопроводе;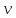
– кинематическая вязкость жидкости; ℓ − длина трубопровода; Q− расход жидкости в трубопроводе; d – внутренний диаметр трубопровода.
При турбулентном режиме ( Re >2300 ) используют формулу Дарси Скорость течения жидкости обычно выражают через расход
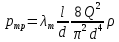 ,
,
где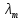 − коэффициент сопротивления трения; Q – расход жидкости; d – диаметр трубопровода; ???? − плотность жидкости.
− коэффициент сопротивления трения; Q – расход жидкости; d – диаметр трубопровода; ???? − плотность жидкости.
Коэффициент сопротивления трения λт , при турбулентном режиме, в общем случае эависит от числа Рейнольдса Re и относительной шероховатости ∆ / d . Если для так называемых гидравлически гладких труб шероховатость на сопротивление не влияет, то коэффициент λт, одноэначно определяется числом Re . Наиболее употребительной для этого случая является формула Блазиуса
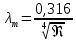 .
.
Универсальной формулой, учитывающей одновременно оба фактора, является формула Альтшуля
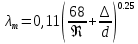 .
.
При малых значениях Re и ∆ / d вторым слагаемым в этой формуле можно принебречь. Наоборот, при больших Re и ∆ / d первое слагаемое становится ничтожно малым и она принимает вид формулы Шифринсона
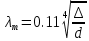 .
.
Суммарная потеря давления Σ∆???? в трубопроводе гидропривода складывается из потерь на трение по длине и местных потерь:
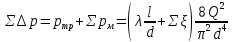 .
.
Пример расчёта.
В гидротормозной системе автомобиля передача усилия Fот ножной педали к тормозам колёс производится посредством жидкости, вытесняемой поршнем 1 из главного тормозного цилиндра 2 по трубопроводам в рабочие тормозные цилиндры передних 3 и задних 4 колёс. На первом этапе торможения за счёт хода поршней рабочих цилиндров выбирается зазор между тормозными колодками и барабанами. На втором этапе торможения происходит сжатие всего объёма жидкости V в системе, выравнивание давления и прижатие колодок к барабанам. Диаметры всех цилиндров одинаковы. Определить : 1) скорости перемещения поршней колёсных тормозных цилиндров для передних (υ
п) и эадних (υз); 2) ход педали, необходимый для упругого сжатия тормозной жидкости в системе. Плотность жидкости ???? , модуль объёмной упругости 1/????р, жидкость – минеральное масло, вязкостью ????.
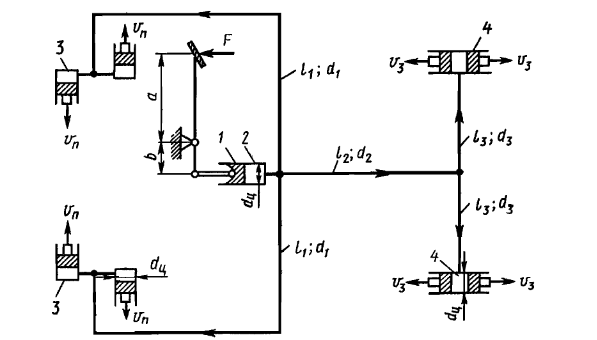
Рисунок 4. Схема тормозной системы автомобиля
Дано: F =500 H; dц=22 мм; α/b=5; ℓ 1 =2 м; ℓ 2 =3м; ℓ 3 = 1м;
d1 =4мм; d2 =5мм; d3 =4мм; V=0,5л; ???? = 1000кг/м3; ???? = 0,1∙10-3м2/с;
1/????р =103МПа.
Решение:
Для решения используем формулу сжимаемости жидкости
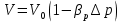 ,
,
где V – конечный объём жидкости, V0 – начальный объём жидкости,
∆???? – увеличение давления, ????р – коэффициент объёмного сжатия.
Задаёмся режимом течения, основываясь на роде жидкости – значении вязкости (вода, бензин, керосин – режим обычно турбулентный; масла – ламинарный). Потери напора в гидролиниях при ламинарном режиме определяют по закону Пуазейля
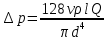 .
.
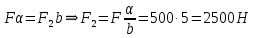 .
.
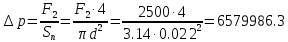 Па.
Па.
Это давление передаётся во все гидролинии.
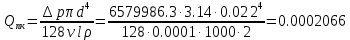 м3/с
м3/с
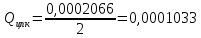 м3/с.
м3/с.
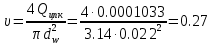 м/с.
м/с.
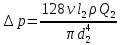
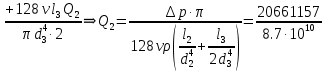
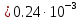
м3/с
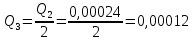 м3/с.
м3/с.
Q4 =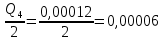 м3/с.
м3/с.
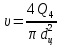
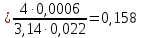 м/с
м/с
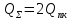 +
+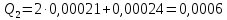 м3/с.
м3/с.
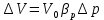 ,
,
Где ∆V – изменение объёма = V0 – V.
∆V =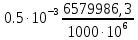 =0,033
=0,033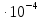 м3
м3
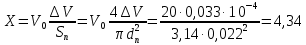 см.
см.


 Задания и методические указания
Задания и методические указания
к выполнению самостоятельной работы
Самостоятельное задание должно выполняется студентом после проработки изложенного выше материала дисциплины. Студенту предлагается самостоятельно решить четыри задачи. В каждой задаче исходные данные выбираются из соответствующих таблиц по шифру зачётной книжки студента. При выполнении задания необходимо соблюдать следующие требования:
На первой странице тетради привести в табличной форме исходные данные для решения каждой задачи согласно шифру - номеру зачетной книжки студента.
Обязательно перед решением записать условие задачи и содержание контрольного вопроса в тетрадь. Решение сопровождать кратким пояснительным текстом, в котором должно быть указано: какая величина определяется и по какой формуле, какие величины подставляются в формулу (из условия задачи, из учебника, задачника, определена ранее и т.д.). Вычисления представлять в развернутом виде.
Обязательно проставлять размерности всех заданных и рассчитанных величин в международной системе СИ.
Графический материал должен быть выполнен четко, в масштабе и на миллиметровой бумаге, как исключение можно использовать бумагу в клеточку.
При использовании таблиц, формул и других справочных материалов, необходимо непосредственно при решении задачи указывать ссылку на литературный источник в квадратных скобках, например - [6].
После решения задачи должен быть произведен краткий анализ полученных результатов и сделаны соответствующие выводы
Таблица выбора данных к задаче №1
(исходные данные выбираются из таблицы по последней цифре зачётной книжки студента).
где
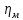 – механический к.п.д. гидропривода, равный произведению механических к.п.д. насоса и гидродвигателя ;
– механический к.п.д. гидропривода, равный произведению механических к.п.д. насоса и гидродвигателя ; 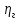 – гидравлический к.п.д., равный отношению потерь давления в гидролиниях к давлению на выходе из насоса.
– гидравлический к.п.д., равный отношению потерь давления в гидролиниях к давлению на выходе из насоса. 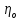 − объёмный к.п.д. гидропривода.
− объёмный к.п.д. гидропривода.К.п.д. гидропривода с дроссельным управлением помимо перечисленных потерь учитывает и к.п.д. системы управления , который равен отношению мощности потока жидкости , подведённого к гидродвигателю, к мощности потока жидкости на выходе из насоса без учёта потерь в гидролиниях.
При последовательном включении дросселя
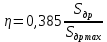 ,
,при параллельном включении дросселя
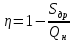 ,
,здесь Sдр и Sдр max − соответственно текущая и максимальная величина площади проходного сечения дросселя; Qдр − расход через дроссель.
Гидроприводы при расчётах можно рассматривать как сложные трубопроводы с насосной подачей,, а гидродвигатели − как особые местные сопротивления , вызывающие потерю давления
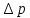 . Эта величина считается независящей от расхода жидкости (скорости перемещения выходного звена поршня) . Для гидроцилиндров величина
. Эта величина считается независящей от расхода жидкости (скорости перемещения выходного звена поршня) . Для гидроцилиндров величина 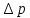 приближённо определяется как частное от деления нагрузки вдоль штока на площадь поршня со стороны нагнетания При расчёте указанных схем следует учитывать то, что расход жидкости на входе в гидроцилиндр с односторонним штоком отличен от расхода на выходе, так как площади поршня различны.
приближённо определяется как частное от деления нагрузки вдоль штока на площадь поршня со стороны нагнетания При расчёте указанных схем следует учитывать то, что расход жидкости на входе в гидроцилиндр с односторонним штоком отличен от расхода на выходе, так как площади поршня различны.В основе расчёта трубопроводов лежат формула Дарси ,для определения потерь напора на трение по длине потока и формула Вейсбаха для расчёта местных потерь.
При ламинарном режиме ( Re < 2300) удобнее пользоваться формулой Пуазейля
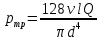 ,
,где pтр – потеря давления на трение в трубопроводе;
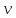
– кинематическая вязкость жидкости; ℓ − длина трубопровода; Q− расход жидкости в трубопроводе; d – внутренний диаметр трубопровода.
При турбулентном режиме ( Re >2300 ) используют формулу Дарси Скорость течения жидкости обычно выражают через расход
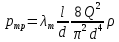 ,
,где
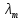 − коэффициент сопротивления трения; Q – расход жидкости; d – диаметр трубопровода; ???? − плотность жидкости.
− коэффициент сопротивления трения; Q – расход жидкости; d – диаметр трубопровода; ???? − плотность жидкости.Коэффициент сопротивления трения λт , при турбулентном режиме, в общем случае эависит от числа Рейнольдса Re и относительной шероховатости ∆ / d . Если для так называемых гидравлически гладких труб шероховатость на сопротивление не влияет, то коэффициент λт, одноэначно определяется числом Re . Наиболее употребительной для этого случая является формула Блазиуса
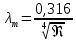 .
.Универсальной формулой, учитывающей одновременно оба фактора, является формула Альтшуля
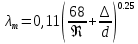 .
.При малых значениях Re и ∆ / d вторым слагаемым в этой формуле можно принебречь. Наоборот, при больших Re и ∆ / d первое слагаемое становится ничтожно малым и она принимает вид формулы Шифринсона
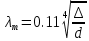 .
.Суммарная потеря давления Σ∆???? в трубопроводе гидропривода складывается из потерь на трение по длине и местных потерь:
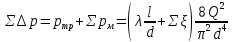 .
.Пример расчёта.
В гидротормозной системе автомобиля передача усилия Fот ножной педали к тормозам колёс производится посредством жидкости, вытесняемой поршнем 1 из главного тормозного цилиндра 2 по трубопроводам в рабочие тормозные цилиндры передних 3 и задних 4 колёс. На первом этапе торможения за счёт хода поршней рабочих цилиндров выбирается зазор между тормозными колодками и барабанами. На втором этапе торможения происходит сжатие всего объёма жидкости V в системе, выравнивание давления и прижатие колодок к барабанам. Диаметры всех цилиндров одинаковы. Определить : 1) скорости перемещения поршней колёсных тормозных цилиндров для передних (υ
п) и эадних (υз); 2) ход педали, необходимый для упругого сжатия тормозной жидкости в системе. Плотность жидкости ???? , модуль объёмной упругости 1/????р, жидкость – минеральное масло, вязкостью ????.

Рисунок 4. Схема тормозной системы автомобиля
Дано: F =500 H; dц=22 мм; α/b=5; ℓ 1 =2 м; ℓ 2 =3м; ℓ 3 = 1м;
d1 =4мм; d2 =5мм; d3 =4мм; V=0,5л; ???? = 1000кг/м3; ???? = 0,1∙10-3м2/с;
1/????р =103МПа.
Решение:
Для решения используем формулу сжимаемости жидкости
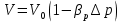 ,
,где V – конечный объём жидкости, V0 – начальный объём жидкости,
∆???? – увеличение давления, ????р – коэффициент объёмного сжатия.
Задаёмся режимом течения, основываясь на роде жидкости – значении вязкости (вода, бензин, керосин – режим обычно турбулентный; масла – ламинарный). Потери напора в гидролиниях при ламинарном режиме определяют по закону Пуазейля
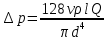 .
.-
Определим силу давления F2 на шток поршня главного тормозного цилиндра. Составим уравнение момента относительно оси поворота педали.
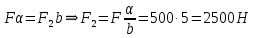 .
.-
Определим давление в главном тормозном цилиндре по формуле
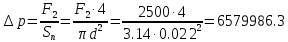 Па.
Па.Это давление передаётся во все гидролинии.
-
Определим расход в гидролинях передних колёс, используя формулу Пуазейля
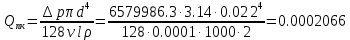 м3/с
м3/с-
Определим расход в тормозном цилиндре передних колёс разделив общий расход пополам
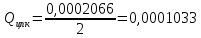 м3/с.
м3/с.-
Определим скорость перемещения поршня в тормозном цилиндре передних колёс
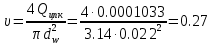 м/с.
м/с.-
Определим расход Q2 в общей линии задних колёс , используя формулу Пуазейля
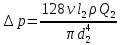
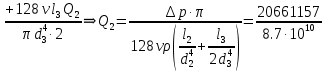
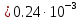
м3/с
-
Определим расход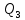 в линии задних колёс
в линии задних колёс
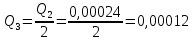 м3/с.
м3/с.-
Определим расход Q4 в тормозном цилиндре задних колёс
Q4 =
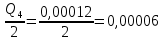 м3/с.
м3/с.-
Определим скорость движения поршня в тормозном цилиндре задних колёс
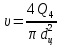
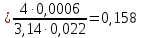 м/с
м/с-
Определить суммарный расход масла в главном тормозном цилиндре
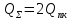 +
+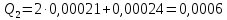 м3/с.
м3/с.-
Определим изменение объёма масла в системе при упругом сжатии по формуле
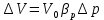 ,
,Где ∆V – изменение объёма = V0 – V.
∆V =
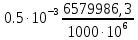 =0,033
=0,033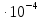 м3
м3-
Определим ход педали
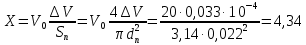 см.
см.

 Задания и методические указания
Задания и методические указанияк выполнению самостоятельной работы
Самостоятельное задание должно выполняется студентом после проработки изложенного выше материала дисциплины. Студенту предлагается самостоятельно решить четыри задачи. В каждой задаче исходные данные выбираются из соответствующих таблиц по шифру зачётной книжки студента. При выполнении задания необходимо соблюдать следующие требования:
На первой странице тетради привести в табличной форме исходные данные для решения каждой задачи согласно шифру - номеру зачетной книжки студента.
Обязательно перед решением записать условие задачи и содержание контрольного вопроса в тетрадь. Решение сопровождать кратким пояснительным текстом, в котором должно быть указано: какая величина определяется и по какой формуле, какие величины подставляются в формулу (из условия задачи, из учебника, задачника, определена ранее и т.д.). Вычисления представлять в развернутом виде.
Обязательно проставлять размерности всех заданных и рассчитанных величин в международной системе СИ.
Графический материал должен быть выполнен четко, в масштабе и на миллиметровой бумаге, как исключение можно использовать бумагу в клеточку.
При использовании таблиц, формул и других справочных материалов, необходимо непосредственно при решении задачи указывать ссылку на литературный источник в квадратных скобках, например - [6].
После решения задачи должен быть произведен краткий анализ полученных результатов и сделаны соответствующие выводы
Таблица выбора данных к задаче №1
(исходные данные выбираются из таблицы по последней цифре зачётной книжки студента).
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| А, МПа | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 1 | 1,2 | 1,3 | 1,4 |
| D, мм | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 600 | 650 | 700 |
| d,мм | 5 | 5 | 10 | 10 | 10 | 15 | 15 | 20 | 20 | 25 |
| ℓ,мм | 15 | 15 | 20 | 20 | 25 | 25 | 30 | 30 | 35 | 35 |
| a/b | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 |