Файл: Отчет по лабараторной работе 1. 4 дисциплины Метрология, стандартизация и сертификация.docx
Добавлен: 23.11.2023
Просмотров: 73
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица №3 Результаты наблюдений
| Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениями | |||
| Наименование | Значение U= 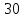 мВ мВ | ||
| Число многократных наблюдений | 11 | 20 | 29 |
| Среднее арифметическое результатов наблюдений, мВ | 30,0047 | 29,9690 | 29,9710 |
| Оценка СКО ряда наблюдений, мВ | 0,0437 | 0,0716 | 0,0635 |
| Оценка СКО результата измерения, мВ | 0,0132 | 0,0160 | 0,0118 |
| Вычисление доверительных границ погрешности результата измерения | |||
| Доверительная вероятность | 0.990 | ||
| Квантиль распределения Стьюдента | 3,1693 | 2,8609 | 2,7632 |
| Доверительные границы случайной составляющей погрешности результата измерений, мВ | 0,0417 | 0,0458 | 0,0326 |
| Предел допускаемой абсолютной погрешности средства измерений (инструментальная погрешность), мВ Расчетное значение: | 0,0490 | 0,0490 | 0,0490 |
| Отношение предела допускаемой абсолютной погрешности средства измерения к доверительной границе случайной составляющей погрешности результата измерений | 1,1739 | 1,0691 | 1,5030 |
| Доверительные границы абсолютной погрешности результата измерений, мВ | 0,0644 | 0,0671 | 0,0589 |
| Результаты измерений | 30,0047 0 | 29,9690 0 | 29,9710 0 |
Ответы на контрольные вопросы:
1. При многократных опытах для обнаружения грубых погрешностей используют статистические критерии, т. е. «подозрительные» значения сравнивают с некоторым статистическим критерием.
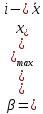
где
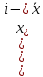 – максимально возможное отклонение от среднего;
– максимально возможное отклонение от среднего; 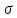 – среднеквадратичное значение ряда наблюдений.
– среднеквадратичное значение ряда наблюдений.Последовательность оценки по данному методу:
- упорядочить значения наблюдений;
- найти отклонения:
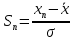 ,
, 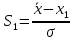
- результаты сравниваются с предельным отклонением
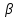 для данного распределения случайной величины, которое берется из справочных данных для конкретного числа наблюдений и принятого уровня значимости α. При
для данного распределения случайной величины, которое берется из справочных данных для конкретного числа наблюдений и принятого уровня значимости α. При 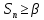 (
(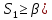 результат считают анормальным и исключают.
результат считают анормальным и исключают. 2. Исправленный результат измерений – значение физической величины, полученное при помощи средства измерений и уточненное путем введения в него необходимых поправок.
3. Абсолютная погрешность – это разность между показанием прибора и действительным значением. Действительное значение – значение, полученного прибором более высокого класса точности.
Относительной погрешностью – это отношение абсолютной погрешности измерения к показанию прибора. Обычно выражается в процентах.
Приведенная погрешность — это относительная погрешность, выраженная отношением абсолютной погрешности к условно принятому значению нормирующей величины (xn). Нормирующее значение – конечное значение шкалы (предел измерений).
4. Систематической погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остаётся постоянной или закономерно меняется. Не исключенная систематическая погрешность результата образуется из не исключенных систематических погрешностей: погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений, инструментальные погрешности, зависящие от погрешностей применяемых средств измерений, погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, личные погрешности, обусловленные индивидуальными особенностями наблюдателя. По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.
Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.
Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.
Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.
Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.
При равномерном распределении не исключенных составляющих систематической погрешности, границы вычисляются по формуле:
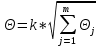
где
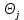 – граница j-ой составляющей не исключенной систематической погрешности; k – коэффициент, определяемый доверительной вероятностью (при P=0.95 k=1.1, при P=0.99 k=1.4).
– граница j-ой составляющей не исключенной систематической погрешности; k – коэффициент, определяемый доверительной вероятностью (при P=0.95 k=1.1, при P=0.99 k=1.4). Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом. Оценку случайных погрешностей осуществляют путем определения границ интервала, накрывающего с заданной вероятностью случайные погрешности. Границы такого интервала называют доверительными границами, а сам интервал – доверительным интервалом. Вероятность попадания случайной погрешности в доверительный интервал называют доверительной вероятностью или надежностью измерений в данных границах.
Если закон распределения случайных погрешностей известен, то доверительная вероятность Р находится:
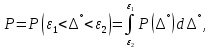
где
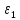 и
и 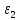 – нижняя и верхняя границы доверительного интервала погрешностей;
– нижняя и верхняя границы доверительного интервала погрешностей;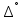
- случайная погрешность;
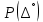 - плотность вероятности случайных погрешностей (закон распределения).
- плотность вероятности случайных погрешностей (закон распределения).5. Анализируя работы измерительной установки, могут быть выявлены систематические погрешности. Систематические погрешности определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения.
6. При равномерном распределении не исключенных составляющих систематической погрешности, границы вычисляются по формуле:

где
 – граница j-ой составляющей не исключенной систематической погрешности; k – коэффициент, определяемый доверительной вероятностью (при P=0.95 k=1.1, при P=0.99 k=1.4).
– граница j-ой составляющей не исключенной систематической погрешности; k – коэффициент, определяемый доверительной вероятностью (при P=0.95 k=1.1, при P=0.99 k=1.4). 7. Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
При числе результатов наблюдений n > 50 для проверки принадлежности их к нормальному распределению по НТД предпочтительным является один из критериев: χ2 Пирсона или ω2 Мизеса - Смирнова.
При числе результатов наблюдений 50 > n > 15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.
При числе результатов наблюдений
Доверительные границы ɛ (без учета знака) случайной погрешности результата измерения находят по формуле
ɛ=tS(Ǎ) ,
где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по таблице.
8. Оценка СКО ряда наблюдений характеризует разброс результатов
, полученных в различных наблюдениях из-за случайных погрешностей. Оценка СКО результата измерения характеризует погрешность определения среднего значения измеряемой величины.
9. Результат эксперимента представляется с указанием единиц измерения.
Также должны быть указаны характеристики погрешностей измерения:
1) указываются границы суммарной погрешности и доверительная вероятность, с которой погрешность находится в этих границах;
2) отдельно указываются характеристики случайной и систематической составляющих погрешности.
3) Погрешность измерения должна выражаться не более чем двумя значащими цифрами. Можно указать одну значащую цифру, если погрешность округления не превышает 5 % (погрешность округляют в большую сторону).
4) Критерий округления результата измерения: последний разряд результата должен быть таким же, как у округленного значения абсолютной погрешности.
5) Результат измерения должен включать в себя условия проведения измерения.