ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Исследовать на сходимость и абсолютную сходимости:
а)
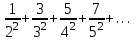
б)
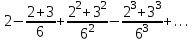
Решение:
а) Запишем ряд с общим членом:
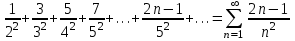
Применением интегральный признака Коши. Функция
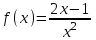- не отрицательна при 
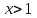и монотонно убывает, тогда 
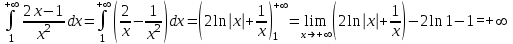- т.е. интеграл расходится. Тогда по интегральному признаку Коши расходится и ряд 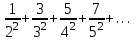.б) Запишем ряд с общим членом:
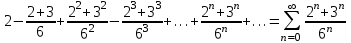.Исследуем данный ряд с помощью признака Даламбера. Здесь
, 
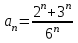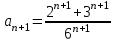. Применяем признак Даламбера: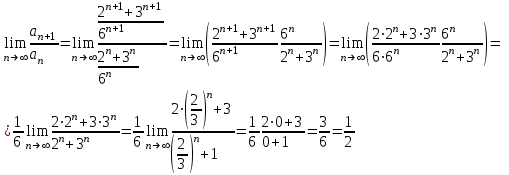
Получили
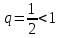. По признаку Даламбера ряд сходится.Ответ: а) расходится; б) сходится.
3. Найти область сходимости рядов:
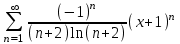
Решение:
По признаку Даламбера ряд сходится, если
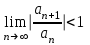, где 
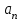- общий член ряда.Тогда
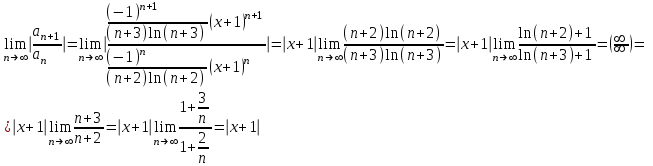
Из последнего следует, что
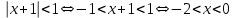
Таким образом интеграл сходимости:
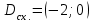. *** При
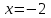, получаем числовой знакоположительный ряд 
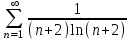который расходится, так как по интегральному признаку Коши расходится и интеграл:
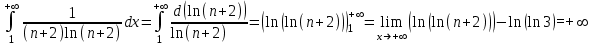.*** При
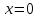, получаем числовой знакочередующийся ряд
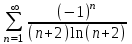который сходится условно, так как ряд из модулей расходится: 
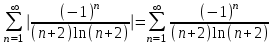. А ряд 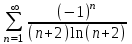сходится по признаку Лебница, общий член ряда по абсолютному значению 
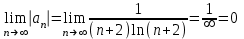стремится к нулю, причем монотонно:
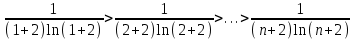.Таким образом, область сходимости первоначального ряда будет:
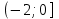.Ответ:
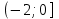- область сходимости ряда. 4. Разложить функцию в ряд Тейлора по степеням
: 
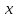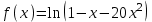.Решение:
Ряд Тейлора по степеням
: 
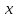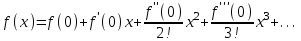
Вычисляем
;
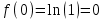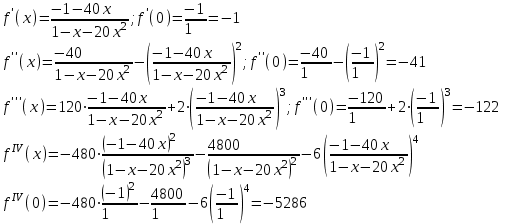
и т.д.
Получаем разложение
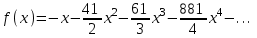
Ответ:
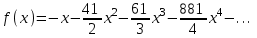
5. Вычислить
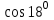с точностью до 0,0001.Решение:
Воспользуемся известным разложением в ряд Тейлора функции
,
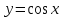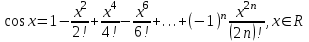.Тогда
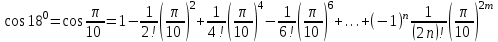
Полученный числовой ряд есть ряд знакочередующийся, удовлетворяющий условиям теоремы Лейбница. Следовательно, чтобы вычислить требуемое значение с точностью
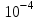, достаточно взять всего три члена ряда, при этом ошибка будет меньше 4-го члена:
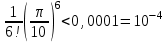.Таким образом, с требуемой точностью
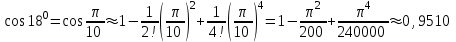
Ответ:
.
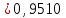
6. Взяв три члена разложения в степенной ряд подынтегральной функции, вычислить
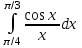.Оценить погрешность полученного результата.
Решение:
Разложим подынтегральную функцию в ряд Маклорена, для этого в основное разложение косинуса
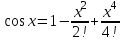взяв три члена ряда, разделив каждое слагаемое на 
получим разложение подынтегральной функции: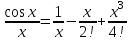
.Этот ряд можно интегрировать в любых конечных пределах, т.е.
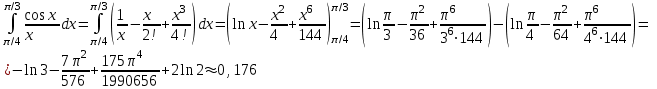
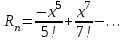. Для оценки погрешности используем признак Лейбница:
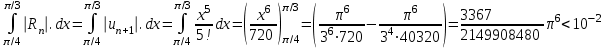.Ответ:
, 
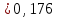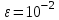.7. Решить дифференциальное уравнение
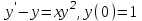.Определить три ненулевых члена разложения в ряд решения.
Решение:
Ищем решение этой задачи Коши в виде ряда Маклорена:
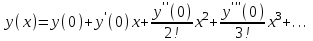
По условию
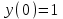, далее поочередно вычисляем:
;
;
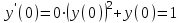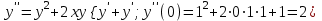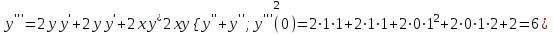и т.д.Таким образом получаем разложение в степенной ряд:
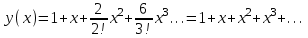
Ответ:
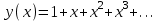
8. Разложить в ряд Фурье функцию
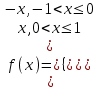.Решение:
Разложим функцию в ряд Фурье на промежутке
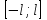
по формуле
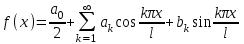, где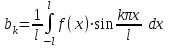 
, 
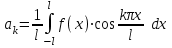
У нас
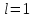, тогда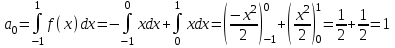 
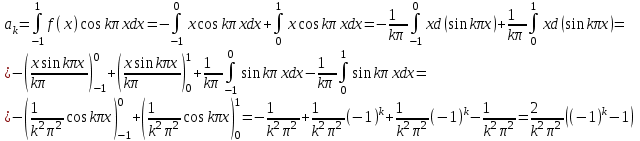
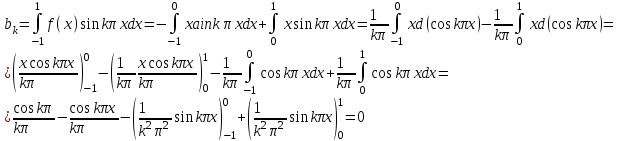
Таким образом, имеем следующее разложение функции:
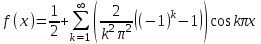
Ответ:
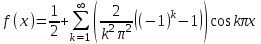.377. Найти координаты центра тяжести однородной плоской фигуры, ограниченной кривой
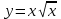, с осью 
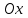и прямой 
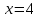.Решение:
Координаты центра тяжести однородной плоской фигуры найдем по формулам:
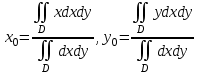.Изобразим область интегрирования:
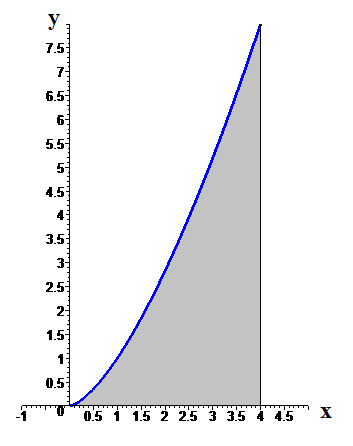
При изменении значения
от 0 до 4, значения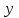 
меняются от 0 до 
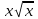. Вычислим двойные интегралы перейдя к повторным:
;
;
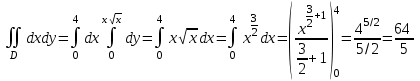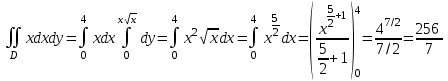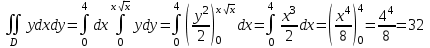.Находим координаты центра тяжести:
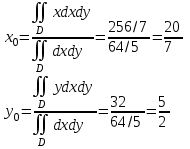
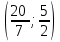- координаты центра тяжести.Ответ:
.
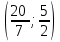