Министерство науки и образования РФ

Волгоградский государственный технический университет

Кафедра «Нефтегазовые сооружения»

Курсовой проект на тему:
«Расчет морской стационарной платформы сквозного типа»

Вариант 6

Выполнил:
ст. гр. МНС-1-18
Борисенко М. Б.
Проверил:
Габова В.В.

Волгоград 2020

Исходные данные:
Район 3 Подрайон 2
Размер базы 25х15 м Глубина 20 м
Нагрузка на палубу 2

Максимальные скорости ветра, м/с:
При двухминутном интервале осреднения V₍₂₎: 46 м/с
При десятиминутном интервале осреднения V₍₁₀₎: 38 м/с

1. Определение клиренса
Отметка нижней части надводных строений морской стационарной платформы, отсчитываемая от нуля Кронштадтского футштока определяется по:
Н_кл = Н_{у, max} + 1,1ħ_0,1 + Δh_set + H_пр

H_пр – наибольшая высота прилива. H_пр = 1,35 м
Н_{у, max} – наивысший годовой уроень моря обеспеченностью 1%, м, отсчитываемый от нуля Кронштадтского футштока. Н_{у, max} = 1,6 м
ħ_0,1 – высота волны. ħ_0,1 = 12,3 м
Δh_set – высота ветрового нагона (СП 38.13330.2012 прил. Б1)
Δh_set = d( )
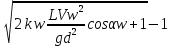α_w – угол между продольной осью водоема и направление ветра, град.
сosα_w = 1
V_w – расчетная скорость ветра, м/с;
L – длина разгона. L = k_vis
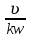
k_w = 3(1+0,3V_w)∙10^-7
V_w = k_flk_lV_l
k_fl – коэффициент пересчета данных по скоростям ветра, измеряемый по флюгеру, принимаемы по формуле k_fl = 0,675 + 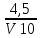, но не более 1.
k_l – коэффициент приведение скорости ветра к условиям водной поверхности. k_l = 1,09

k_fl = 0,675 + 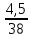= 0,79
V_w = 0,79∙1,09∙38 = 32,72
k_w = 3(1+0,3∙32,72) ∙ 10^-7 = 32,448∙10^-7
L = 5∙10¹¹∙ 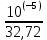= 0,153∙10⁶
Δh_set = 20(

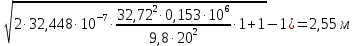
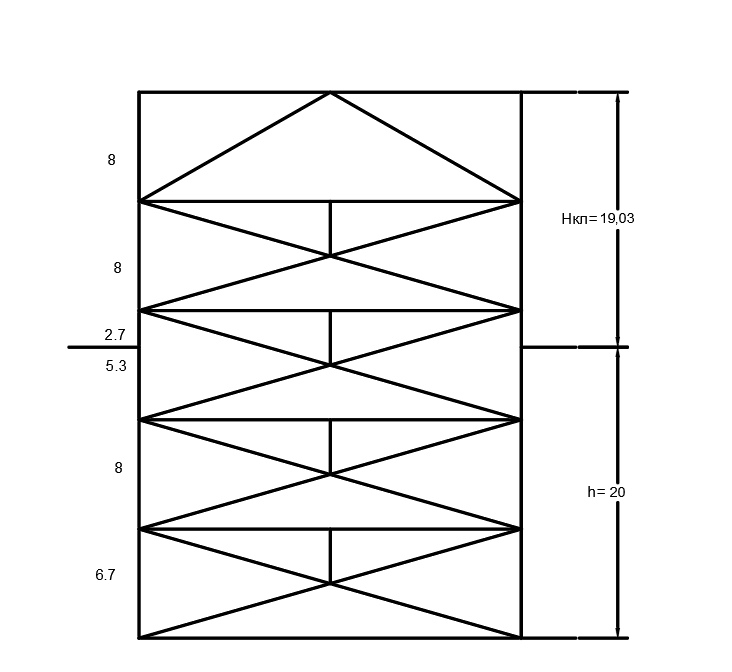
Н_кл = 1,6 + 1,1∙12,3 + 2,55 + 1,35 = 19,03 м

Принимаем Н_кл = 19,1 м.

Общая высота Н = Нкл + d = 19,1 + 20 = 39,1 м.

---

2. Снеговые нагрузки
Нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия следует определять по [1] п.10:

S₀ = с_eс_tμSg, где
с_e - коэффициент, учитывающий снос с него с покрытий зданий под действием ветра или иных факторов, принимаемый в соответствии с п.10.5. с_e = 1.
с_t - термический коэффициент, принимаемый в соответствии с п.10.10. c_t = 1
μ - коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, принимаемый в соответствии с п.10.4. μ = 1.
Sg - вес снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемый в соответствии с п.10.2. Sg = 1,5 кН/м².
S₀ = 1∙1∙1∙1,5 = 1,5 кПа
S = 35∙25 = 875 м²
F = S∙S0 = 875∙1,5 = 1312,5 кН
F₁ = F₂ = F₃ = F₄ = 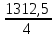= 328,125 кН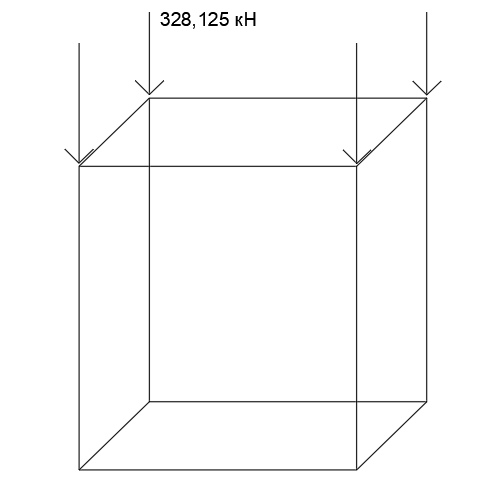


3. Воздействия ветра
Нормативное значение среде составляющей ветровой нагрузки w_m в зависимости от эквивалентной высоты z_e над поверхностью земли следует определять по [1] п.11:
W_m = W₀k(z_e)c ,
где W₀ – нормативное значение ветрового давления. W₀ = 0,38 кПа
k(z_e) - коэффициент, учитывающий изменение ветрового давления для высоты z_e
k(z_e): при 5 = 0,75;
10 = 1;
19,1 = 1,2275;
c – аэродинамический коэффициент
c_t = c_x(1+η)k₁,
где с_x – определяется так же, как и для отдельно стоящей фермы;
η - определяется так же, как и для ряда плоских ферм; η = 0,95;


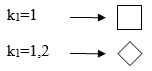
c_xi – аэродинамический коэффициент i-го элемента конструкций, определяемый в соответствии с указаниями B.1.12;
A_i – площадь проекции i-го элемента конструкции;
A_k – площадь, ограниченная контуром конструкции.
К_λ = 1;
А_к= Нкл×15 = 19,03×15 = 285,45 м²
А^пояса = 15×0,63×3 = 28,35 м²
А^стойки= 19,03×1,02×2 = 38,82 м²
А^{раскоса}= (2×5,74+2×17+2×11+4+2,7) ×0,426 = 31,601 м

---

²
С_х = К_λ∙С_х∞;
С_х∞ определяется по [1], рисунок В.17 в зависимости от числа R_e и отношения шероховатости .
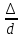стойка = 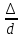= = 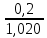0,000196

пояс = 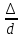= = 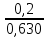0,000317

раскос = 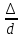= = 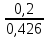0,000469
Re - Число Рейнольдса определяется по [1], В.1.11.
Re=0.88×d√(Wo ×K(z_e) × γ_f)×10⁵
где d, м, - диаметр сферы;
W₀, Па, - определяется в соответствии с 11.1.4;
k(z_e) - определяется в соответствии с 11.1.6;
Y_f - коэффициент надежности по нагрузке, см. 11.1.12. Y_f = 1,4;
Re=0.88×1,02√(0,38×10³×1,228×1,4) × 10⁵ = 23×10⁵
Re=0.88×0,63√(0,38×10³×1,228×1,4) × 10⁵ = 14,2×10⁵
Re=0.88×0.426√(0,38×10³×1,228×1,4) ×10⁵ = 9,6×10⁵
C_х∞^стойка = 0,48; C_хi^стойка = 0,48;
C_х∞^пояс = 0,93; C_хi^пояс = 0,93;
C_х∞^раскос = 1,2; C_хi^раскос = 1,2;
C_х = 0,29
С_t = 0,29×(1+0,95)×1 = 0,566;
С_t = 0,29×(1+0,95)×1,2 = 0,679;
W_m = 0,38×0,75×0,566 = 0,161;
W_m = 0,38×1×0,566 = 0,215;
W_m = 0,38×1,2275×0,566 = 0,264;
W_m = 0,38×0,75×0,679 = 0,194;
W_m = 0,38×1×0,679 = 0,258;
W_m = 0,38×1,2275×0,679 = 0,317;

Активная составляющая нагрузки:
При z=5; W = 0,161×7,5×0,8 = 0,966 кН/м;

---

При z=10; W = 0,215×7,5×0,8 = 1,29 кН/м;
При z=19,1; W = 0,264×7,5×0,8 = 1,584 кН/м;
Пассивная составляющая нагрузки:
При z=5; W = 0,161×7,5×0,6 = 0,7245 кН/м;
При z=10; W = 0,215×7,5×0,6 = 0,9675 кН/м;
При z=19,1; W = 0,264×7,5×0,6 = 1,188 кН/м;


Активная составляющая нагрузки (1,2,3 стойки):
1 стойка: W = 0,194×3,86×0,8 = 0,599 кН/м;
W = 0,258×3,86×0,8 = 0,797 кН/м;
W = 0,317×3,86×0,8 = 0,979 кН/м;
2 стойка: W = 0,194×14,58×0,8 = 2,263 кН/м;
W = 0,258×14,58×0,8 = 3,009 кН/м;
W = 0,317×14,58×0,8 = 3,698 кН/м;
3 стойка: W = 0,194×10,72×0,8 = 1,664 кН/м;
W = 0,258×10,72×0,8 = 2,213 кН/м;
W = 0,317×10,72×0,8 = 2,719 кН/м;
Пассивная составляющая нагрузки (3,4,1 стойки):
3 стойка: W = 0,194×3,86×0,6 = 0,499 кН/м;
W = 0,258×3,86×0,6 = 0,598 кН/м;
W = 0,317×3,86×0,6 = 0,734 кН/м;
4 стойка: W = 0,194×14,58×0,6 = 1,697 кН/м;
W = 0,258×14,58×0,6 = 2,257 кН/м;
W = 0,317×14,58×0,6 = 2,773 кН/м;
1 стойка: W = 0,194×10,72×0,6 = 1,248 кН/м;
W = 0,258×10,72×0,6 = 1,659 кН/м;
W = 0,317×10,72×0,6 = 2,039 кН/м;

4. Волновая нагрузка
Нагрузки от волн на обтекаемые преграды и сквозные сооружения.
Нагрузки от волн на вертикальную обтекаемую преграду.
[2] Е.1 Максимальная сила воздействия волн max Q , кН, на вертикальную обтекаемую преграду с поперечными размерами a ≤ 0,4λ и b ≤ 0,4λ при глубине d > dcr определяется из ряда значений, получаемых при различных удалениях æ = x/λ вершины волны от преграды, 1 ряд æ = x/λ = 0; 2 ряд æ = x/λ = 0,11 по формуле:
Q_max =Q_{i, max}δ_i + Q_{v, max}δ_v
где Qi, max и Qv, max – соответственно инерционный и скоростной компоненты силы воздействия волн, кН:
Q_{i, max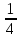} = ρgπb²hК_vα_iβ_i;
Q_{i, max} = 0,25∙1,015∙9,81∙3,14∙1,020²∙12,3∙1∙0,975∙1 = 97,425 кН;
Q_{v, max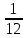} = ρgbh²К_v²α_vβ_v;
Q_{v, max} = 0,083∙9,81∙1,015∙1,020∙12,3² ∙1²∙2,45∙0,65 = 203,705 кН;
1 ряд: δ_i =0, δ_v =1; 2 ряд: δ_i =1,08, δ_v =0,18 – коэффициенты сочетания инерционного и скоростного компонентов максимальной силы от воздействия волн, принимаемые соответственно по графикам 1 и 2 рисунка Е.1;
h =12,3 и λ = 155 – высота и длина расчетной волны;
a = 1,02 – размер преграды по лучу волны, м;
b = 1,02 – размер преграды по фронту волны, м;
k_v = 1 – коэффициент перехода от действительных значений скорости и ускорения волнового потока, воздействующего на преграду, к их средним значениям (таблице Е.1);
α_i = 0,975 и α_v = 2,45 – инерционный и скоростной коэффициенты глубины, принимаемые соответственно по графикам а и б рисунка Е.2;

---

βi = 1 и βv = 0,65 – инерционный и скоростной коэффициенты формы преграды с поперечным сечением в виде круга, эллипса и прямоугольника, принимаемые по графикам рисунка Е.3.
1 ряд: Q_max = Q_{v, max} = 203,705 кН;
2 ряд: Q_max = 97,425∙1,08 + 203,705∙0,18 = 141,886 кН;
[2] Е2. Линейную нагрузку от волн q, кН/м, на вертикальную обтекаемую преграду на глубине z, при максимальной силе от воздействия волн Q_max (рис.8, а) следует определять по формуле:

где q_{i, max} и q_{v, max} - инерционный и скоростной компоненты максимальной линейной нагрузки от волн, кН/м, определяемые по формулам:


δ_xi и δ_xv – коэффициенты сочетания инерционного и скоростного компонентов нагрузки от волн, принимаемые соответственно по графикам 1 и 2 рисунка Е.4 при значении æ согласно Е.1;
θ_xi и θ_xv – коэффициенты компонентов волновой нагрузки, принимаемые по графикам а и б рисунка Е.5 при значениях относительной глубины

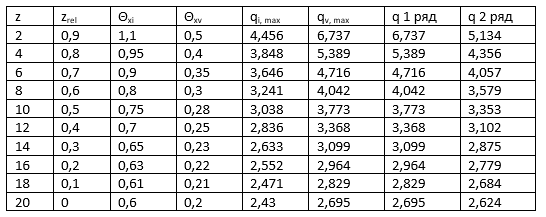
[2] Е.3 Превышение взволнованной поверхности η, м, над расчетным уровнем должно определяться по формуле

где η_rel относительное превышение взволнованной поверхности, определяемое по рисунку Е.6.
1 ряд: η_rel = -0,61;
2 ряд: η_rel = -0,18;
[3] Е.5 Расстояние z_Qmax , м, от расчетного уровня воды до точки приложения максимальной силы от воздействия волн на вертикальную обтекаемую преграду Qmax определяется по формуле:

где δi и δv – коэффициенты, принимаемые по графикам 1 и 2 рисунка Е.1 при значении æ, соответствующем Qmax;
z_Qi и z_Qv – ординаты точек приложения соответственно инерционного и скоростного компонентов сил

---

Смотрите также файлы

• Согласованоутверждаю.pdf

• Сыныбы 6 сынып Сынып жетекшісі.docx

• Государственное бюджетное специальное (коррекционное) образовательное учреждение школа интернат 2.doc

• Сыныбы 8 Сынып жетекшісі.docx

• Внешняя политика в первой трети 16 в..docx