Файл: Расчет морской стационарной платформы сквозного типа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 92
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, м, определяемые по формулам:
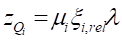
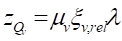
где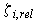 = 0,058,
= 0,058, 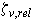 = 0,01 - относительные ординаты точек приложения инерционного и скоростного компонентов сил, принимаемые по графикам рисунка Е7;
= 0,01 - относительные ординаты точек приложения инерционного и скоростного компонентов сил, принимаемые по графикам рисунка Е7;
1 ряд: μi = 0,67; μv = 1; 2 ряд: μi = 0,89; μv = 1,5 – инерционный и скоростной коэффициенты фазы, принимаемые по графикам рисунка Е.8.
1 ряд стоек: zQi = 6,023; zQv = 1,55; ZQmax = 1,55;
2 ряд стоек: zQi = 8,001; zQv = 2,325; ZQmax = 4,55;
Нагрузки от волн на горизонтальную обтекаемую преграду.
[2] Е.11 Максимальное значение равнодействующей нагрузки от волн Pmax, кН/м, на горизонтальную обтекаемую преграду (рисунок 8,б) с поперечными размерами a ≤ 0,1λ, м, и b ≤ 0,1λ, м, при zc ≤ b, но (zc–b/2) > h/2 и при (d–zc) ≥ b должно определяться по формуле:
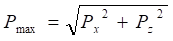
для двух случаев:
- с максимальной горизонтальной составляющей нагрузки Px,max, кН/м, при соответствующем значении вертикальной составляющей нагрузки Pz, кН/м;
- с максимальной вертикальной составляющей нагрузки Pz,max, кН/м, при соответствующем значении горизонтальной составляющей линейной Px, кН/м.
Расстояние x, м, от вершины волны до центра преграды при действии максимальных нагрузок Px,max и Pz,max должны определяться по относительной величине æ=x/λ, принимаемой согласно рисункам Е.4 и Е.11;
[2] Е.12 Максимальное значение горизонтальной составляющей нагрузки от волн Px,max, кН/м, на горизонтальную обтекаемую преграду определяется из ряда величин, получаемых при различных значениях æ, по формуле
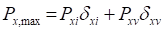
где Pxi и Pxv – инерционный и скоростной компоненты горизонтальной составляющей нагрузки от волн, кН/м, определяемые по формулам:
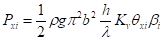
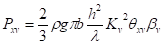
δxi и δxv – коэффициенты сочетания инерционного и скоростного компонентов нагрузки от волн, принимаемые соответственно по графикам 1 и 2 рисунка Е.4 при значении æ согласно Е.1;
1 ряд: δxi= 0; δxv= 1
2 ряд: δxi= 0,88; δxv= 0,18
θxi и θxv – то же, что и в Е.2;
βi и βv – инерционный и скоростной коэффициенты формы преграды с поперечным сечением в виде круга, эллипса и прямоугольника, принимаемые по графикам рисунка Е.3 при значениях a/b – для горизонтальной и b/a – для вертикальной составляющих нагрузки.

[2] Е.13 Максимальное значение вертикальной составляющей нагрузки от волн на горизонтальную обтекаемую преграду Pz,max, кН/м, следует определять из ряда величин, получаем при разных значениях æ по формуле
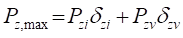
где Pzi и Pzv – инерционный и скоростной компоненты вертикальной составляющей нагрузки от волн, кН/м, определяемые по формулам:
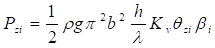
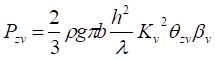
δzi и δzv – инерционный и скоростной коэффициенты сочетания, принимаемые по графикам 1 и 2 рисунка Е.11.
1 ряд: δzi= 1; δzv= 0;
2 ряд: δzi= 0,32; δzv= 0,72;
θzi и θzv – коэффициенты компонентов волновой нагрузки, принимаемые соответственно по графикам в и г рисунка Е.5 при значениях относительной ординаты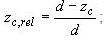

Гидростатическое давление на элементы опорного блока.
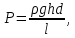 где ρ-плотность воды (1,015 кг/м3);
где ρ-плотность воды (1,015 кг/м3);
g –ускорение свободного падения (9,81 м/с2);
h –глубина расположения элемента;
d –диаметр элемента;
l – длина труб;
Пояса: l= 15
Р5,3=1,015∙9,81∙0,63∙5,3/15= 2,216 кН\м;
Р13,3=1,015∙9,81∙0,63∙13,3/15= 5,562 кН\м;
Р20=1,015∙9,81∙0,63∙20/15= 8,364 кН\м;
Раскосы: l5,3= 11,26;l13,3= 17;l20= 16,43;
Р5,3=1,015∙9,81∙0,426∙2,65/11,26 = 0,997 кН\м;
Р13,3=1,015∙9,81∙0,426∙9,3/17 = 2,318 кН\м;
Р20=1,015∙9,81∙0,426∙16,65/16,43 = 4,294 кН\м;
Выталкивающая сила, действующая на элементы.
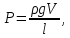 где ρ-плотность воды (1,015 кг/м^3);
где ρ-плотность воды (1,015 кг/м^3);
g –ускорение свободного падения (9,81 м/с^2);
V-объем элемента;
l –длина труб;
Пояса:
Vп =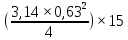 = 4,67 м3;
= 4,67 м3;
Рп= 1,015∙9,81∙4,67= 46,499 кН;
Раскосы:
V5,3=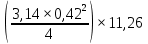 = 1,56 м3;
= 1,56 м3;
Р5,3= 1,015∙9,81∙1,56= 15,533 кН;
V13,3= V20=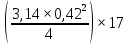 = 2,35 м3;
= 2,35 м3;
Р13,3= Р20= 1,015∙9,81∙2,35= 23,399 кН;
5. Расчет элементов стальных конструкций при центральном растяжении и сжатии. Расчет элементов сплошного сечения.
[3] Расчет на прочность элементов из стали с нормативным сопротивлением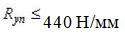 при центральном растяжении или сжатии силой N следует выполнять по формуле:
при центральном растяжении или сжатии силой N следует выполнять по формуле: 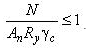
Площадь элемента конструкции находят по:
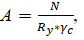
Где N-сила при центральном сжатии;
Ry-расчетное сопротивление стали сжатию;
γс-коэффициент условий работы (γс=1);
Сталь: С245: Ry= 240 Н/мм2;
Сила при центральном сжатии, N: -Стойки: 7293,1 кН;
-Раскосы: 2405,1 кН;
- Пояса: 893,1 кН;
- Внутр. пояса: 520,9 кН;
Площадь элемента конструкции:
- Стойки: А=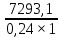 = 303875,5 мм2= 303,87 см2;
= 303875,5 мм2= 303,87 см2;
- Раскосы: А=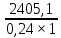 = 10021,25 мм2= 100,21 см2;
= 10021,25 мм2= 100,21 см2;
- Пояса: А=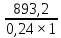 = 721,67 мм2= 37,22 см2;
= 721,67 мм2= 37,22 см2;
- Внутр. пояса: А=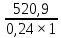 = 2170,42 мм2= 21,7 см2;
= 2170,42 мм2= 21,7 см2;
 [3] Проверку элемента конструкции на устойчивость выполняют с помощью формулы:
[3] Проверку элемента конструкции на устойчивость выполняют с помощью формулы:
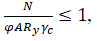
Где φ-коэффициент устойчивости при центральном сжатии, значение которого при ????̅ ≥0,6 следует определять по формуле: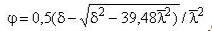
Значение коэффициента δ в формуле следует вычислять по формуле:
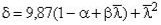
где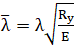 - условная гибкость стержня;
- условная гибкость стержня;
Е- модуль упругости (2,1∙105 МПа= 2,1∙1011 Н/м2;
α и β- коэффициенты, определяемые по таблице 7 [4] в зависимости от типов сечений;
α= 0,03; β= 0,06;
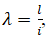 Где λ-гибкость;
Где λ-гибкость;
l-длинна элемента;
i-момент инерции.
Проверка элемента конструкции на устойчивость:
- Стойки: из [4] диаметр внешний, d= 920 мм;
толщина стенки, t=11 мм;
радиус инерции сечения, i= 32,14 см= 0,3214 м;
площадь поперечного сечения, А= 314,13 см2;
λ=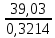 = 121,44; l= 39,03 м;
= 121,44; l= 39,03 м;
λ=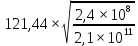 = 4,11;
= 4,11;
δ= 9,87∙(1-0,03+0,06∙4,11)+4,112= 28,9;
φ=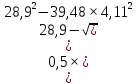 = 1,94;
= 1,94;
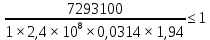 ;
;
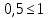 ;
;
 - Раскосы: из [4] диаметр внешний, d= 630 мм;
- Раскосы: из [4] диаметр внешний, d= 630 мм;
толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=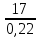 = 77,27 м; l= 17 м;
= 77,27 м; l= 17 м;
λ=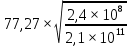 = 2,61;
= 2,61;
δ= 9,87∙(1-0,03+0,06∙2,61)+2,612= 17,93;
φ=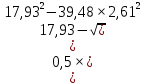 = 0,78;
= 0,78;
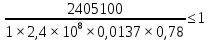 ;
;
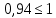 ;
;
 - Пояса: из [4] диаметр внешний, d= 630 мм;
- Пояса: из [4] диаметр внешний, d= 630 мм;
толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=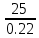
= 113,64 м; l= 25 м;
λ=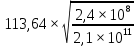 = 3,84;
= 3,84;
δ=9,87∙(1-0,03+0,06∙3,84)+3,842=26,6;
φ=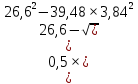 =0,52;
=0,52;
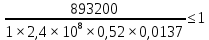 ;
;
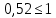 ;
;
 - Внутр. пояса: из [4] диаметр внешний, d= 630 мм;
- Внутр. пояса: из [4] диаметр внешний, d= 630 мм;
толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=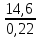 = 66,36 м; l= 14,6 м;
= 66,36 м; l= 14,6 м;
λ=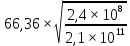 = 2,24;
= 2,24;
δ= 9,87∙(1-0,03+0,06∙2,24)+2,242= 15,92;
φ=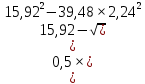 = 0,85;
= 0,85;
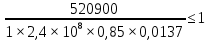 ;
;
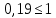 ;
;
Расчет сварного соединения.
[3] Расчет сварного соединения с угловыми швами, при действии силы N, проходящей через центр тяжести соединения, следует выполнять на срез (условный) по одному из двух сечений (рисунок 20) по формулам:
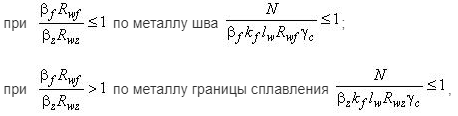
где ????????- расчетная длина швов в сварном соединении, равная суммарной длине всех его участков за вычетом по 1 см на каждом непрерывном участке шва;
????????,???????? - коэффициенты, принимаемые по таблице 39.
???????? – катет углового шва;
???????????? –расчетное сопротивление угловых швов срезу (условному) по металлу границы сплавления;
???????????? –расчетное сопротивление угловых швов срезу (условному) по металлу шва;
????с - коэффициент условий работы.
- Стойка: ????????= Ртр- 1см= 3,14∙920- 10= 2888,8- 10= 2878,8 мм;
????????= t∙1,2= 11∙1,2= 13,2 мм;
????с= 1;
????????=1,1 мм, ????????=1,15 мм;
????????????=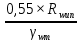 =
=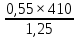 = 180,4;
= 180,4;
????????????=0,45∙Run=0,45∙370= 167;
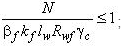
где
1 ряд: μi = 0,67; μv = 1; 2 ряд: μi = 0,89; μv = 1,5 – инерционный и скоростной коэффициенты фазы, принимаемые по графикам рисунка Е.8.
1 ряд стоек: zQi = 6,023; zQv = 1,55; ZQmax = 1,55;
2 ряд стоек: zQi = 8,001; zQv = 2,325; ZQmax = 4,55;
Нагрузки от волн на горизонтальную обтекаемую преграду.
[2] Е.11 Максимальное значение равнодействующей нагрузки от волн Pmax, кН/м, на горизонтальную обтекаемую преграду (рисунок 8,б) с поперечными размерами a ≤ 0,1λ, м, и b ≤ 0,1λ, м, при zc ≤ b, но (zc–b/2) > h/2 и при (d–zc) ≥ b должно определяться по формуле:
для двух случаев:
- с максимальной горизонтальной составляющей нагрузки Px,max, кН/м, при соответствующем значении вертикальной составляющей нагрузки Pz, кН/м;
- с максимальной вертикальной составляющей нагрузки Pz,max, кН/м, при соответствующем значении горизонтальной составляющей линейной Px, кН/м.
Расстояние x, м, от вершины волны до центра преграды при действии максимальных нагрузок Px,max и Pz,max должны определяться по относительной величине æ=x/λ, принимаемой согласно рисункам Е.4 и Е.11;
[2] Е.12 Максимальное значение горизонтальной составляющей нагрузки от волн Px,max, кН/м, на горизонтальную обтекаемую преграду определяется из ряда величин, получаемых при различных значениях æ, по формуле
где Pxi и Pxv – инерционный и скоростной компоненты горизонтальной составляющей нагрузки от волн, кН/м, определяемые по формулам:
δxi и δxv – коэффициенты сочетания инерционного и скоростного компонентов нагрузки от волн, принимаемые соответственно по графикам 1 и 2 рисунка Е.4 при значении æ согласно Е.1;
1 ряд: δxi= 0; δxv= 1
2 ряд: δxi= 0,88; δxv= 0,18
θxi и θxv – то же, что и в Е.2;
βi и βv – инерционный и скоростной коэффициенты формы преграды с поперечным сечением в виде круга, эллипса и прямоугольника, принимаемые по графикам рисунка Е.3 при значениях a/b – для горизонтальной и b/a – для вертикальной составляющих нагрузки.

[2] Е.13 Максимальное значение вертикальной составляющей нагрузки от волн на горизонтальную обтекаемую преграду Pz,max, кН/м, следует определять из ряда величин, получаем при разных значениях æ по формуле
где Pzi и Pzv – инерционный и скоростной компоненты вертикальной составляющей нагрузки от волн, кН/м, определяемые по формулам:
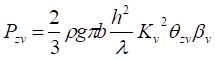
δzi и δzv – инерционный и скоростной коэффициенты сочетания, принимаемые по графикам 1 и 2 рисунка Е.11.
1 ряд: δzi= 1; δzv= 0;
2 ряд: δzi= 0,32; δzv= 0,72;
θzi и θzv – коэффициенты компонентов волновой нагрузки, принимаемые соответственно по графикам в и г рисунка Е.5 при значениях относительной ординаты

Гидростатическое давление на элементы опорного блока.
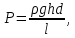 где ρ-плотность воды (1,015 кг/м3);
где ρ-плотность воды (1,015 кг/м3);g –ускорение свободного падения (9,81 м/с2);
h –глубина расположения элемента;
d –диаметр элемента;
l – длина труб;
Пояса: l= 15
Р5,3=1,015∙9,81∙0,63∙5,3/15= 2,216 кН\м;
Р13,3=1,015∙9,81∙0,63∙13,3/15= 5,562 кН\м;
Р20=1,015∙9,81∙0,63∙20/15= 8,364 кН\м;
Раскосы: l5,3= 11,26;l13,3= 17;l20= 16,43;
Р5,3=1,015∙9,81∙0,426∙2,65/11,26 = 0,997 кН\м;
Р13,3=1,015∙9,81∙0,426∙9,3/17 = 2,318 кН\м;
Р20=1,015∙9,81∙0,426∙16,65/16,43 = 4,294 кН\м;
Выталкивающая сила, действующая на элементы.
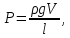 где ρ-плотность воды (1,015 кг/м^3);
где ρ-плотность воды (1,015 кг/м^3);g –ускорение свободного падения (9,81 м/с^2);
V-объем элемента;
l –длина труб;
Пояса:
Vп =
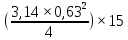 = 4,67 м3;
= 4,67 м3;Рп= 1,015∙9,81∙4,67= 46,499 кН;
Раскосы:
V5,3=
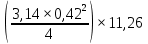 = 1,56 м3;
= 1,56 м3;Р5,3= 1,015∙9,81∙1,56= 15,533 кН;
V13,3= V20=
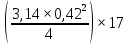 = 2,35 м3;
= 2,35 м3;Р13,3= Р20= 1,015∙9,81∙2,35= 23,399 кН;
5. Расчет элементов стальных конструкций при центральном растяжении и сжатии. Расчет элементов сплошного сечения.
[3] Расчет на прочность элементов из стали с нормативным сопротивлением
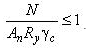
Площадь элемента конструкции находят по:
Где N-сила при центральном сжатии;
Ry-расчетное сопротивление стали сжатию;
γс-коэффициент условий работы (γс=1);
Сталь: С245: Ry= 240 Н/мм2;
Сила при центральном сжатии, N: -Стойки: 7293,1 кН;
-Раскосы: 2405,1 кН;
- Пояса: 893,1 кН;
- Внутр. пояса: 520,9 кН;
Площадь элемента конструкции:
- Стойки: А=
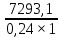 = 303875,5 мм2= 303,87 см2;
= 303875,5 мм2= 303,87 см2;- Раскосы: А=
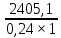 = 10021,25 мм2= 100,21 см2;
= 10021,25 мм2= 100,21 см2;- Пояса: А=
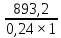 = 721,67 мм2= 37,22 см2;
= 721,67 мм2= 37,22 см2;- Внутр. пояса: А=
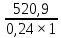 = 2170,42 мм2= 21,7 см2;
= 2170,42 мм2= 21,7 см2; [3] Проверку элемента конструкции на устойчивость выполняют с помощью формулы:
[3] Проверку элемента конструкции на устойчивость выполняют с помощью формулы:
Где φ-коэффициент устойчивости при центральном сжатии, значение которого при ????̅ ≥0,6 следует определять по формуле:
Значение коэффициента δ в формуле следует вычислять по формуле:
где
Е- модуль упругости (2,1∙105 МПа= 2,1∙1011 Н/м2;
α и β- коэффициенты, определяемые по таблице 7 [4] в зависимости от типов сечений;
α= 0,03; β= 0,06;
l-длинна элемента;
i-момент инерции.
Проверка элемента конструкции на устойчивость:
- Стойки: из [4] диаметр внешний, d= 920 мм;
толщина стенки, t=11 мм;
радиус инерции сечения, i= 32,14 см= 0,3214 м;
площадь поперечного сечения, А= 314,13 см2;
λ=
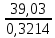 = 121,44; l= 39,03 м;
= 121,44; l= 39,03 м;λ=
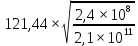 = 4,11;
= 4,11;δ= 9,87∙(1-0,03+0,06∙4,11)+4,112= 28,9;
φ=
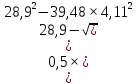 = 1,94;
= 1,94;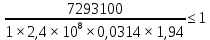 ;
;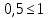 ;
; - Раскосы: из [4] диаметр внешний, d= 630 мм;
- Раскосы: из [4] диаметр внешний, d= 630 мм;толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=
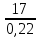 = 77,27 м; l= 17 м;
= 77,27 м; l= 17 м;λ=
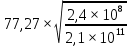 = 2,61;
= 2,61;δ= 9,87∙(1-0,03+0,06∙2,61)+2,612= 17,93;
φ=
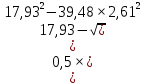 = 0,78;
= 0,78;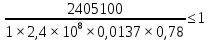 ;
;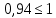 ;
; - Пояса: из [4] диаметр внешний, d= 630 мм;
- Пояса: из [4] диаметр внешний, d= 630 мм;толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=
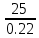
= 113,64 м; l= 25 м;
λ=
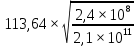 = 3,84;
= 3,84;δ=9,87∙(1-0,03+0,06∙3,84)+3,842=26,6;
φ=
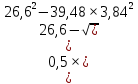 =0,52;
=0,52;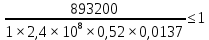 ;
;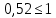 ;
; - Внутр. пояса: из [4] диаметр внешний, d= 630 мм;
- Внутр. пояса: из [4] диаметр внешний, d= 630 мм;толщина стенки, t=7 мм;
радиус инерции сечения, i= 22,03 см= 0,22 м;
площадь поперечного сечения, А= 137 см2;
λ=
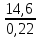 = 66,36 м; l= 14,6 м;
= 66,36 м; l= 14,6 м;λ=
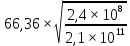 = 2,24;
= 2,24;δ= 9,87∙(1-0,03+0,06∙2,24)+2,242= 15,92;
φ=
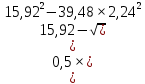 = 0,85;
= 0,85;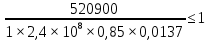 ;
;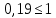 ;
;Расчет сварного соединения.
[3] Расчет сварного соединения с угловыми швами, при действии силы N, проходящей через центр тяжести соединения, следует выполнять на срез (условный) по одному из двух сечений (рисунок 20) по формулам:
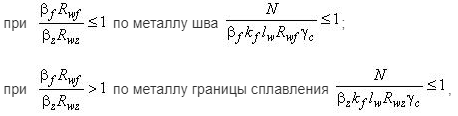
где ????????- расчетная длина швов в сварном соединении, равная суммарной длине всех его участков за вычетом по 1 см на каждом непрерывном участке шва;
????????,???????? - коэффициенты, принимаемые по таблице 39.
???????? – катет углового шва;
???????????? –расчетное сопротивление угловых швов срезу (условному) по металлу границы сплавления;
???????????? –расчетное сопротивление угловых швов срезу (условному) по металлу шва;
????с - коэффициент условий работы.
- Стойка: ????????= Ртр- 1см= 3,14∙920- 10= 2888,8- 10= 2878,8 мм;
????????= t∙1,2= 11∙1,2= 13,2 мм;
????с= 1;
????????=1,1 мм, ????????=1,15 мм;
????????????=
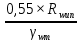 =
=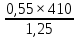 = 180,4;
= 180,4;????????????=0,45∙Run=0,45∙370= 167;