ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема: «Виды распределения дискретных случайных величин»
Ниже приведены важнейшие законы распределения для дискретных случайных величин
Биномиальный закон распределения дискретной случайной величины
Дискретная случайная величина
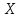имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, 3, …, 
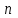с вероятностями:
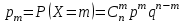,где
, 
, 
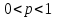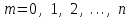.Случайная величина
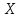, распределённая по биномиальному закону, является числом «успехов» с вероятностью 
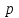в схеме Бернулли при проведении 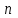независимых опытов.Закон распределения дискретной случайной величины
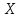, имеющей биномиальное распределение, имеет вид: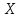| | 0 | 1 | 2 | … |  | … | |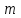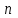
 |  |  |  | … |  | … |  |
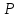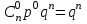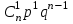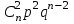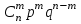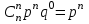Математическое ожидание дискретной случайной величины, имеющей биномиальное распределение, можно вычислить по формуле:
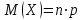.Дисперсию дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле:
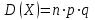.Среднее квадратическое отклонение дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле:
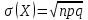.Пример
Производится 3 независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны
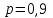. Составить закон распределения дискретной случайной величины 
– числа попаданий по цели. Найти 
, 
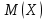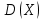и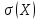 
.Случайная величина
имеет биномиальное распределение с параметрами ,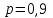 
, 
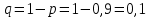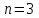.Случайная величина
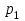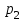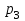принимает значения 0, 1, 2 и 3. Вероятности этих значений 
, 
, 
и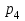 
найдём по формуле для вероятностей биномиального распределения:
;
;
;
.
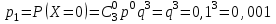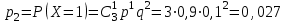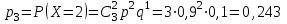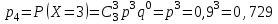
Составим закон распределения дискретной случайной величины
– числа попаданий по цели:| | 0 | 1 | 2 | 3 |
 | 0,001 | 0,027 | 0,243 | 0,729 |
Контроль: 0,001+0,027+0,243+0,729=1.
Значения
, 
и 
найдём двумя способами: а) по закону распределения; б) по готовым формулам.а)
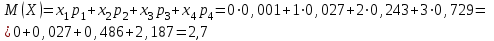
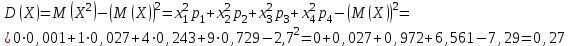
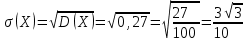
б)
;
;
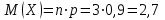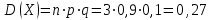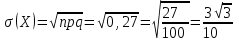.Гипергеометрический закон распределения дискретной случайной величины
Дискретная случайная величина
имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2, …, 
, …, 
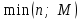с вероятностями:
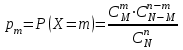,где
, 
, 
, 
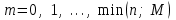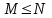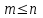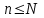, а 
, 
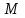и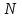 
– натуральные числа.Гипергеометрическое распределение возникает в случаях, подобных следующему:
в урне
шаров, из них 
белых (остальные 
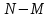чёрные); из урны вынимается шаров. Требуется найти вероятность, что среди извлечённых шаров ровно белых (остальные 
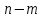чёрные). Случайная величина – число белых шаров среди извлечённых из урны.Математическое ожидание дискретной случайной величины, имеющей гипергеометрическое распределение, можно вычислить по формуле:
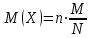.Дисперсию дискретной случайной величины, имеющей гипергеометрическое распределение, можно вычислить по формуле:
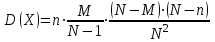.Пример
В классе из 21 ученика 5 девушек. Из этого класса наудачу отбирается 3 ученика. Составить закон распределения дискретной случайной величины
– числа девушек из отобранных учеников. Найти и .В условиях данной задачи:
, 
, 
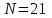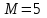. Случайная величина принимает значения 0, 1, 2 и 3. Вероятности этих значений 
, 
, 
и 
найдём по формуле для вероятностей гипергеометрического распределения: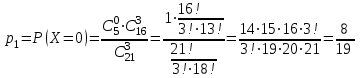
;
;
;
.
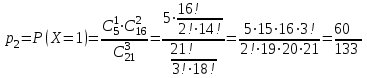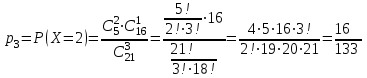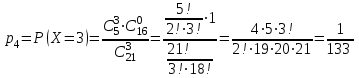
Составим закон распределения дискретной случайной величины
– числа девушек из 3 отобранных учеников:| | 0 | 1 | 2 | 3 |
| |  |  |  |  |
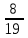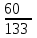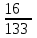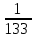Контроль:
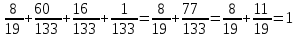.Значения
и найдём двумя способами: а) по закону распределения; б) по готовым формулам.а)
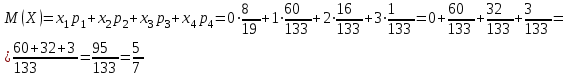
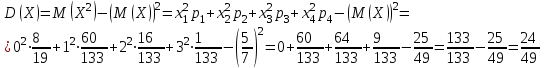
б)
;
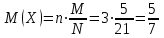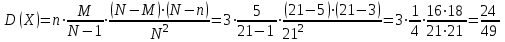.Геометрический закон распределения дискретной случайной величины
Дискретная случайная величина
имеет геометрическое распределение, если она принимает значения 1, 2, 3, 4, … с вероятностями: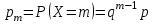
,где
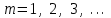
Геометрическое распределение имеет случайная величина
, равная числу опытов в схеме Бернулли, проведённой до первого «успеха» (в единичном опыте вероятность «успеха»: 
, вероятность «неудачи»: 
).Примерами реальных случайных величин