ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; 
; 
.
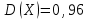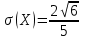3. Симметричная однородная монета подбрасывается до первого выпадения герба. Составьте закон распределения дискретной случайной величины
– числа подбрасываний монеты. Найти 
, 
и 
.
Решение
Подбрасывания монеты производятся независимо друг от друга, вероятность выпадения при разных подбрасываниях одинакова и равна 0,5. Значит, имеет место схема Бернулли, в которой «успехом» считается выпадение герба, а «неудачей» – выпадение цифры.
Так как подбрасывания производятся до первого выпадения герба, то случайная величина , равная числу подбрасываний монеты, имеет геометрическое распределение с параметрам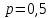и 
и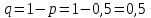 
. Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения:
.
;
;
;
…
;
…
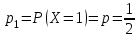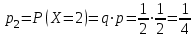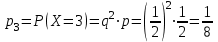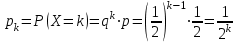Составим закон распределения дискретной случайной величины – числа выстрелов по цели до первого попадания:
Значения , и найдём по готовым формулам.
;
;
.
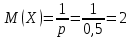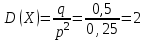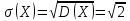Ответ: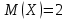
; 
; 
.
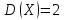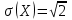!!! Задания для самостоятельного решения (домашнее задание) – фото выслать на электронный адрес mdutkin@mail.ru до 18.00 воскресенья 17 мая:
1. Контрольная работа по теории вероятностей состоит из пяти задач. Вероятность решить правильно каждую задачу для данного ученика равна 0,7. Составьте закон распределения дискретной случайной величины – числа правильно решённых задач. Найти , и .
2. В офисе работают 8 мужчин и 4 женщины. Для работы над проектом создаётся рабочая группа, состоящая из 7 человек. Составьте закон распределения дискретной случайной величины – числа женщин в создаваемой рабочей группе. Найти , и .
3. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины – числа купленных билетов, если теоретически можно купить неограниченное количество билетов. Найти
, и .
4. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины – числа купленных билетов, если можно купить только 4 билета. Найти , и .
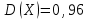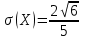; .3. Симметричная однородная монета подбрасывается до первого выпадения герба. Составьте закон распределения дискретной случайной величины
– числа подбрасываний монеты. Найти , и .Решение
Подбрасывания монеты производятся независимо друг от друга, вероятность выпадения при разных подбрасываниях одинакова и равна 0,5. Значит, имеет место схема Бернулли, в которой «успехом» считается выпадение герба, а «неудачей» – выпадение цифры.
Так как подбрасывания производятся до первого выпадения герба, то случайная величина
, равная числу подбрасываний монеты, имеет геометрическое распределение с параметрам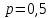и и 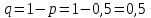. Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: . ; ; ;…
;…
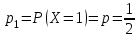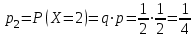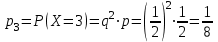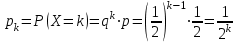Составим закон распределения дискретной случайной величины
– числа выстрелов по цели до первого попадания:| | 1 | 2 | 3 | … |  | … |
 |  |  |  | … |  | … |
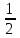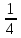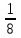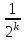Значения
, и найдём по готовым формулам.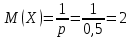 ; ;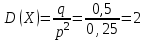 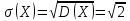.Ответ:
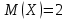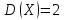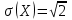; ; .!!! Задания для самостоятельного решения (домашнее задание) – фото выслать на электронный адрес mdutkin@mail.ru до 18.00 воскресенья 17 мая:
1. Контрольная работа по теории вероятностей состоит из пяти задач. Вероятность решить правильно каждую задачу для данного ученика равна 0,7. Составьте закон распределения дискретной случайной величины
– числа правильно решённых задач. Найти , и .2. В офисе работают 8 мужчин и 4 женщины. Для работы над проектом создаётся рабочая группа, состоящая из 7 человек. Составьте закон распределения дискретной случайной величины
– числа женщин в создаваемой рабочей группе. Найти , и .3. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины
– числа купленных билетов, если теоретически можно купить неограниченное количество билетов. Найти
,
и .4. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины
– числа купленных билетов, если можно купить только 4 билета. Найти , и .