ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, распределённых по геометрическому закону, являются:
Закон распределения случайной величины , имеющей геометрическое распределение, имеет вид:
, имеющей геометрическое распределение, имеет вид:
Контроль: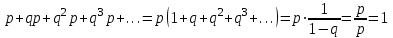 .
.
Вероятности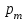 образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим.
образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим.
Математическое ожидание дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: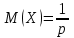 .
.
Дисперсию дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: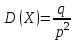 .
.
Среднее квадратическое отклонение дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: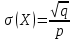 .
.
Пример
Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Составить закон распределения дискретной случайной величины – числа выстрелов по цели до первого попадания. Найти
– числа выстрелов по цели до первого попадания. Найти  ,
, 
и .
.
Случайная величина имеет геометрическое распределение с параметрами
имеет геометрическое распределение с параметрами 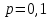 и
и 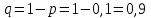 . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения:
. Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения:
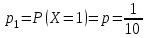 ;
;
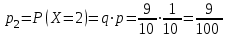 ;
;
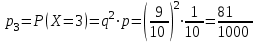 ;
;
…
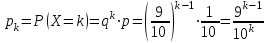 ;
;
…
Составим закон распределения дискретной случайной величины – числа выстрелов по цели до первого попадания:
– числа выстрелов по цели до первого попадания:
Значения ,
,  и
и  найдём по готовым формулам.
найдём по готовым формулам.
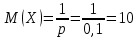 ;
;
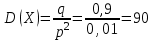 ;
;
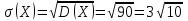 .
.
Задачи
1. Из 25 контрольных работ, среди которых 6 оценены на «отлично», наугад извлекают 4 работы. Составьте закон распределения дискретной случайной величины
 – числа оценённых на «отлично» работ среди четырёх извлечённых. Найти
– числа оценённых на «отлично» работ среди четырёх извлечённых. Найти  ,
,  и
и  .
.
Решение
Данная случайная величина имеет гипергеометрическое распределение с параметрами: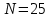 ,
, 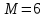 ,
, 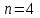 . Случайная величина
. Случайная величина  принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений
принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений  ,
,  ,
,  ,
,  и
и 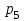 найдём по формуле для вероятностей гипергеометрического распределения:
найдём по формуле для вероятностей гипергеометрического распределения:
 .
.
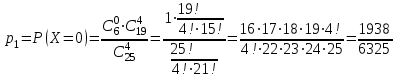 ;
;
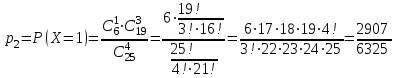 ;
;
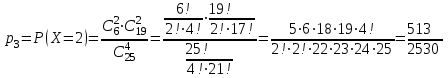 ;
;
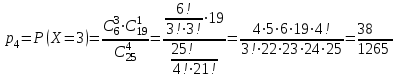 ;
;
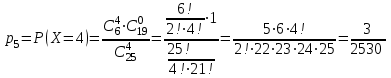 .
.
Составим закон распределения дискретной случайной величины – числа оценённых на «отлично» работ среди четырёх извлечённых:
– числа оценённых на «отлично» работ среди четырёх извлечённых:
Контроль: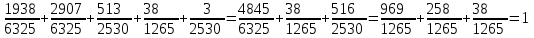 .
.
Значения ,
,  и
и  найдём двумя способами: а) по закону распределения; б) по готовым формулам.
найдём двумя способами: а) по закону распределения; б) по готовым формулам.
а)
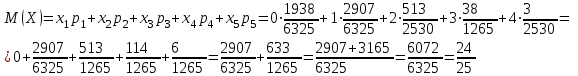
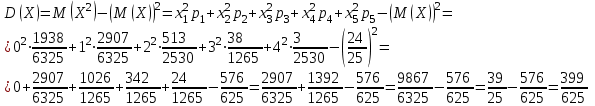
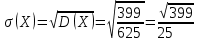
б)
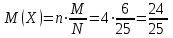 ;
;
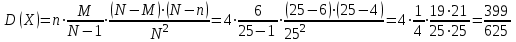 ;
;
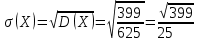 .
.
Ответ: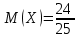 ;
; 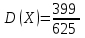 ;
; 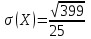 .
.
2. Вероятность попадания баскетбольным мячом в корзину при одном броске равна 0,4. Составьте закон распределения дискретной случайной величины – числа попадания мячом в корзину при четырёх бросках. Найти
– числа попадания мячом в корзину при четырёх бросках. Найти  ,
,  и
и  .
.
Решение
Броски производятся независимо друг от друга, вероятность попадания при разных бросках одинакова и равна 0,4. Значит, имеет место схема Бернулли, в которой «успехом» считается попадание, а «неудачей» – промах. Следовательно, случайная величина , равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами
, равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами 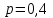 ,
, 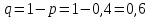 ,
,  .
.
Случайная величина принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений
принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений  ,
,  ,
, 
, и
и  найдём по формуле для вероятностей биномиального распределения:
найдём по формуле для вероятностей биномиального распределения:
 .
.
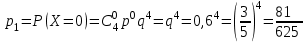 ;
;
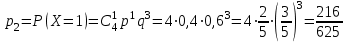 ;
;
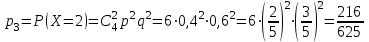 ;
;
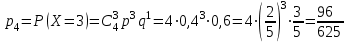 ;
;
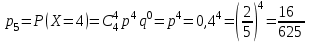
Составим закон распределения дискретной случайной величины – числа попаданий по цели:
– числа попаданий по цели:
Контроль: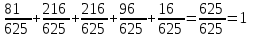 .
.
Значения ,
,  и
и  найдём двумя способами: а) по закону распределения; б) по готовым формулам.
найдём двумя способами: а) по закону распределения; б) по готовым формулам.
а)
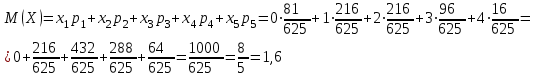
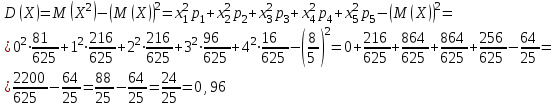
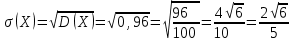
б)
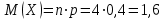 ;
;
 ;
;
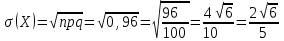 .
.
Ответ: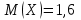
-
число выстрелов до первого попадания; -
число испытаний прибора до первого отказа; -
число бросаний монеты до первого выпадения герба и т.д.
Закон распределения случайной величины
 , имеющей геометрическое распределение, имеет вид:
, имеющей геометрическое распределение, имеет вид:  | 1 | 2 | 3 | … | 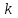 | … |
 |  | 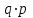 | 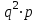 | … | 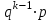 | … |
Контроль:
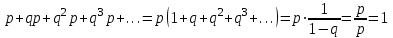 .
.Вероятности
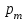 образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим.
образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим.Математическое ожидание дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле:
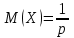 .
.Дисперсию дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле:
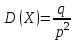 .
.Среднее квадратическое отклонение дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле:
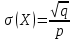 .
.Пример
Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Составить закон распределения дискретной случайной величины
 – числа выстрелов по цели до первого попадания. Найти
– числа выстрелов по цели до первого попадания. Найти  ,
, 
и
 .
.Случайная величина
 имеет геометрическое распределение с параметрами
имеет геометрическое распределение с параметрами 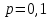 и
и 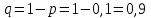 . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения:
. Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: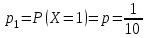 ;
;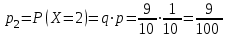 ;
;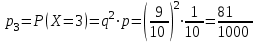 ;
;…
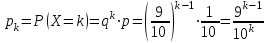 ;
;…
Составим закон распределения дискретной случайной величины
 – числа выстрелов по цели до первого попадания:
– числа выстрелов по цели до первого попадания:  | 1 | 2 | 3 | … |  | … |
 | 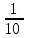 | 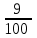 | 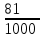 | … | 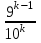 | … |
Значения
 ,
,  и
и  найдём по готовым формулам.
найдём по готовым формулам.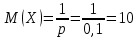 ;
;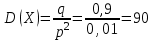 ;
;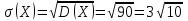 .
.Задачи
1. Из 25 контрольных работ, среди которых 6 оценены на «отлично», наугад извлекают 4 работы. Составьте закон распределения дискретной случайной величины
 – числа оценённых на «отлично» работ среди четырёх извлечённых. Найти
– числа оценённых на «отлично» работ среди четырёх извлечённых. Найти  ,
,  и
и  .
.Решение
Данная случайная величина имеет гипергеометрическое распределение с параметрами:
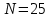 ,
, 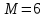 ,
, 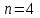 . Случайная величина
. Случайная величина  принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений
принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений  ,
,  ,
,  ,
,  и
и 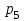 найдём по формуле для вероятностей гипергеометрического распределения:
найдём по формуле для вероятностей гипергеометрического распределения: .
.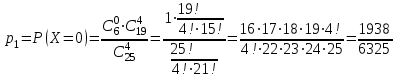 ;
;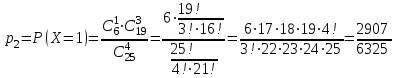 ;
;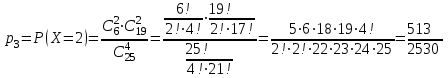 ;
;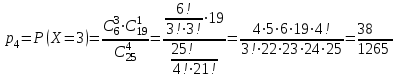 ;
;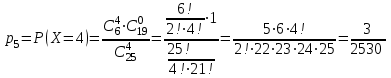 .
.Составим закон распределения дискретной случайной величины
 – числа оценённых на «отлично» работ среди четырёх извлечённых:
– числа оценённых на «отлично» работ среди четырёх извлечённых:  | 0 | 1 | 2 | 3 | 4 |
 | 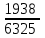 | 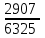 | 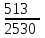 | 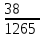 | 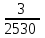 |
Контроль:
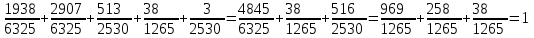 .
.Значения
 ,
,  и
и  найдём двумя способами: а) по закону распределения; б) по готовым формулам.
найдём двумя способами: а) по закону распределения; б) по готовым формулам.а)
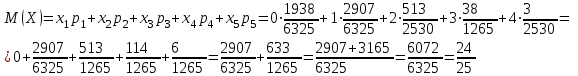
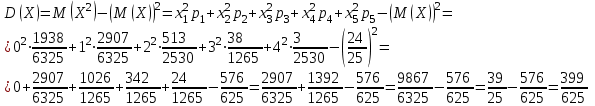
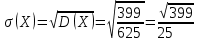
б)
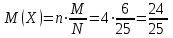 ;
;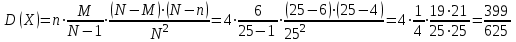 ;
;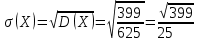 .
.Ответ:
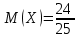 ;
; 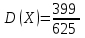 ;
; 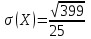 .
.2. Вероятность попадания баскетбольным мячом в корзину при одном броске равна 0,4. Составьте закон распределения дискретной случайной величины
 – числа попадания мячом в корзину при четырёх бросках. Найти
– числа попадания мячом в корзину при четырёх бросках. Найти  ,
,  и
и  .
.Решение
Броски производятся независимо друг от друга, вероятность попадания при разных бросках одинакова и равна 0,4. Значит, имеет место схема Бернулли, в которой «успехом» считается попадание, а «неудачей» – промах. Следовательно, случайная величина
 , равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами
, равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами 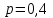 ,
, 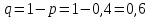 ,
,  .
.Случайная величина
 принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений
принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений  ,
,  ,
, 
,
 и
и  найдём по формуле для вероятностей биномиального распределения:
найдём по формуле для вероятностей биномиального распределения: .
.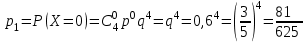 ;
;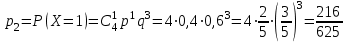 ;
;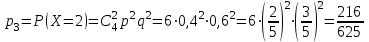 ;
;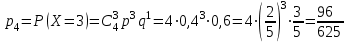 ;
;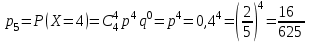
Составим закон распределения дискретной случайной величины
 – числа попаданий по цели:
– числа попаданий по цели:  | 0 | 1 | 2 | 3 | 4 |
 | 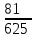 | 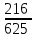 | 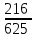 | 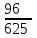 | 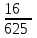 |
Контроль:
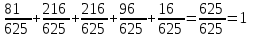 .
.Значения
 ,
,  и
и  найдём двумя способами: а) по закону распределения; б) по готовым формулам.
найдём двумя способами: а) по закону распределения; б) по готовым формулам.а)
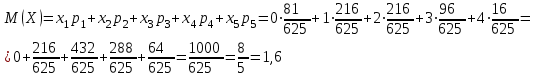
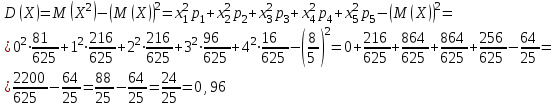
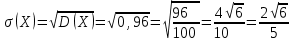
б)
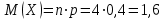 ;
; ;
;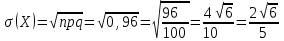 .
.Ответ: