Файл: Герасимов Виктор Олегович Проверил преподаватель Сватов В. Ф. Тюмень Тиу 2023 лабораторная работа 1 Синтез и исследование.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 44

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«Тюменский индустриальный университет» Институт геологии и нефтегазодобычи

Кафедра кибернетических систем

Лабораторные работы

по дисциплине

«Электроника и цифровая схемотехника»

Вариант № 4

Выполнил: ст.гр. АТПбз-20-1

Герасимов Виктор Олегович

Проверил: преподаватель Сватов В.Ф.

Тюмень

Тиу

2023
Лабораторная работа № 1

«Синтез и исследование логических схем цифровых устройств»
1. Цель работы

Ознакомиться с принципами реализации логических функций с помощью логических элементов, провести исследование логических схем, приобрести навыки схемотехнического моделирования на персональных компьютерах.
2. Порядок выполнения работы
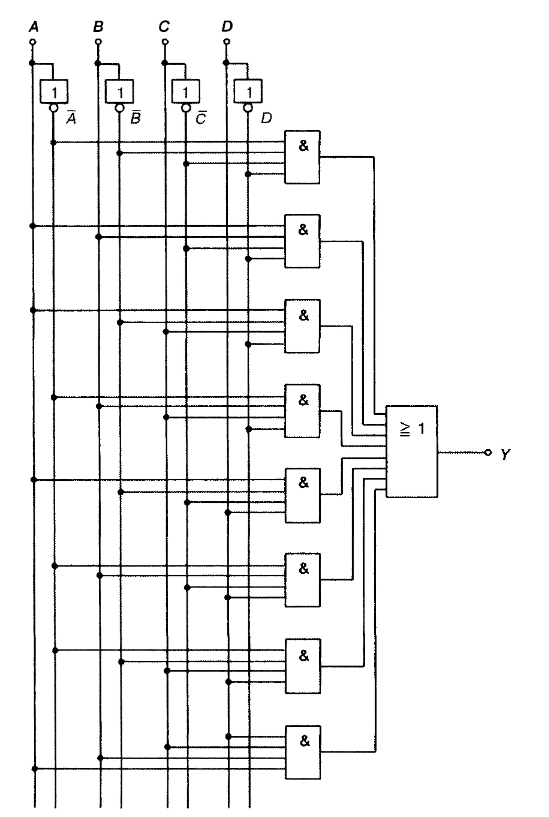
Задание 1. По заданной функции, которая описывает роботу комбинационного устройства, необходимо синтезировать логическую схему минимальной сложности из логических элементов заданного базиса.

Выбор варианта задания осуществляется из табл. 1 по номеру рабочего места.

Таблица 1

Вариант


4
2 3 4 6 9 11 12 14


Примечание: для парных вариантов задается базис “И-НЕ”, для непарных – “ИЛИ-НЕ”
Порядок выполнения работы:

1) Записать аналитическое выражение для булевой функции четырех переменных в СДНФ и СКНФ.

2. Минимизировать полученные выражения СДНФ с помощью карт Карно или диаграмм Вейча и проверить результаты минимизации с помощью Electronics Workbench.


3. К минимизированной функции применить правило де Моргана.

4. Записать минимизированную структурную формулу в заданном базисе. На основе структурной формулы каждой логической операции ставится в соответствие логический элемент выбранного базиса и осущевстляются необходимые связи между элементами комбинационного устройства.

5. Оценить степень сложности схемы. Степень сложности схемы обычно оценивают общим числом ИМС данного типа и суммарным числом входов ЛЭ.

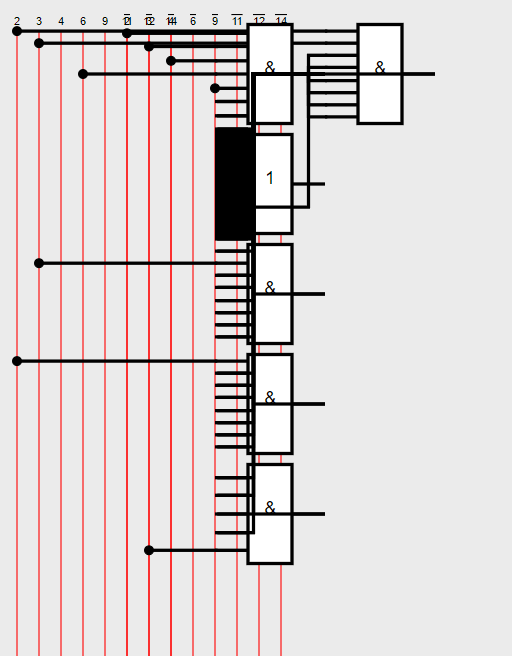
Задание 2. Построить схему комбинационного устройства на ЛЭ заданного базиса и провести исследования с помощью Electronics Workbench.

Порядок выполнения работы:

  1. Собрать схему на ЛЭ заданного базиса в среде Electronics Workbench.

  2. Схема должна иметь четыре входа, например, А,В,С,D и один выход Y. Для большей наглядности добавте светодиоды , подключив их в точках схемы А,В,С,D и Y.

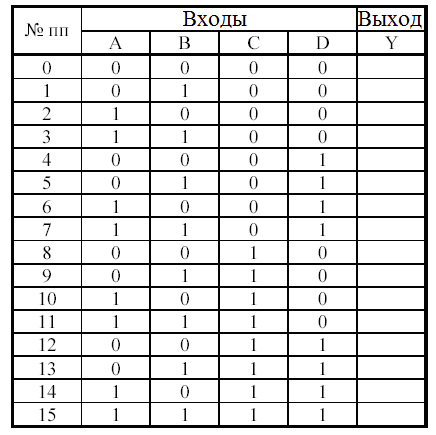
3. Включить моделирование. Нажимая клавиши А,В,С,D, следить за состоянием светодиодных индикаторов на входах и выходе схемы. Сложить таблицу истинности.


Вывод: любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение.
Лабораторная работа № 2
Исследование базовых схем логических элементов цифровых устройств
1. Цель работы

Ознакомиться с принципами работы базовых логических элементов транзисторно-транзисторной логики (ТТЛ) и элементов на униполярных транзисторах (МОП), провести исследования логических элементов, приобрести навыки схемотехнического моделирования на персональных компьютерах.
2. Порядок выполнения работы

Задание 1. Исследование логических элементов транзисторно-транзисторной логики. Откройте файл ewb>. Установите номиналы и обозначения элементов схемы в соответствии с приведенными на рис.1. Схема четыре входа А,В,С,D и один выход Y. Для большей наглядности добавьте светодиоды, подключив их к точкам схемы А,В,С,D и Y. Входи А и В являются входами одной логической схемы И, а входи С та D – входами другой логической схемы И. Благодаря роли транзистора VT1 эти схемы объединены функцией ИЛИ-НЕ. Выходной усилитель реализован на транзисторах VT3, VT4.

Включаем моделирование. Нажимая клавиши А,В,С,D, следим за состоянием светодиодных индикаторов на входах и выходе схемы.



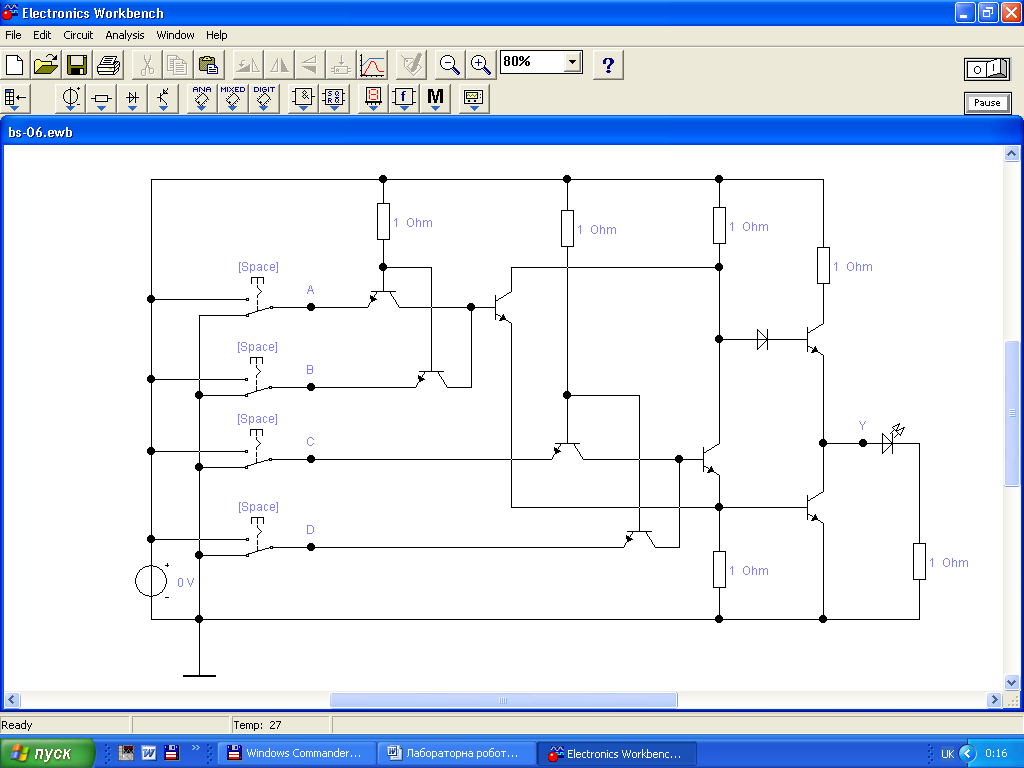
Рис.1

Задание 2. Исследование логических элементов на униполярных транзисторах. Откройте в начале файл <МОП1.ewb>, затем файл <МОП2.ewb>. Выставьте номиналы и обозначения элементов схем в соответствии с приведенными на рис.2,3. Подключите к точкам схемы А,В,Y индикаторы логического уровня.

Включаем моделирование. Нажимая клавиши А и В, следим за состоянием индикаторов на входе и выходе схемы. Составляем таблицу истинности.



Рис.2

Входы
Выход

А
В

0
0
0

0
1
1

1
0
1

1
1
1





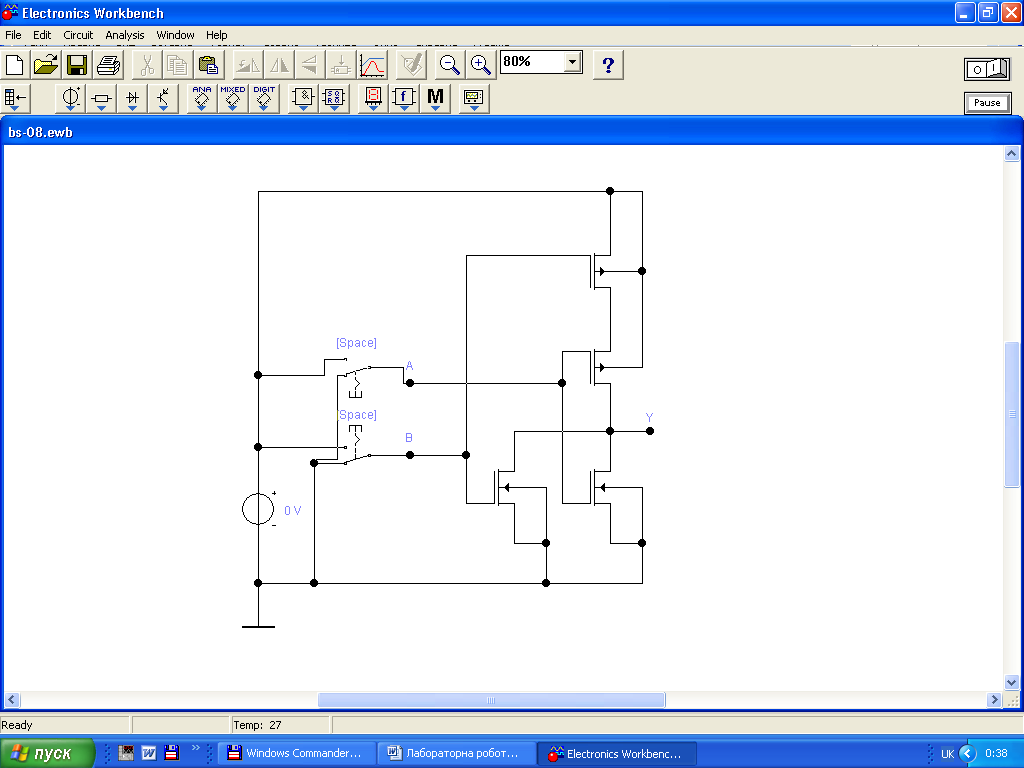
Рис.3


Входы
Выход

А
В

0
0
0

0
1
0

1
0
1

1
1
1


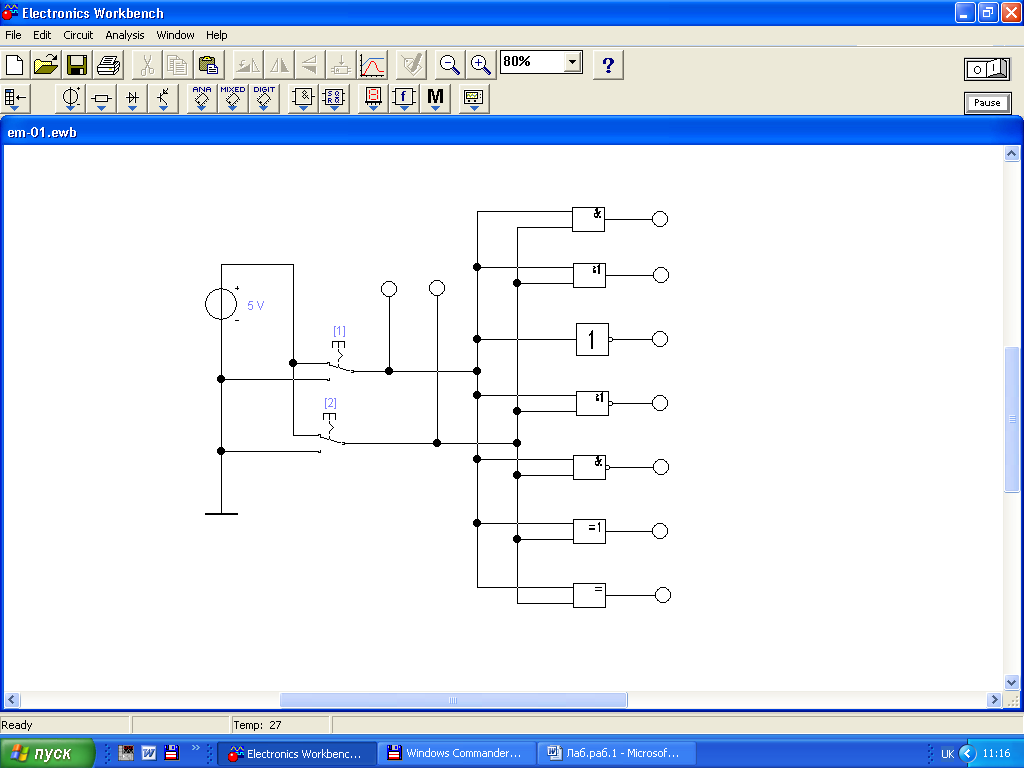
Задание 3. Исследование логических схем ( ручной режим). Откройте файл ewb>. Изображение схемы имеет вид, представленный на рис.4. Подавая высокий и низкий логические уровни ( нажимая по очереди клавиши 1 и 2 клавиатуры компьютера) на входы изображенных логических схем И, ИЛИ, НЕ, ИЛИ-НЕ, И-НЕ, Исключение ИЛИ, Исключение ИЛИ-НЕ, заполнить таблицу истинности.



Рис. 2.6. Набор базовых логических схем


Входы
Выход

1
2
1
2
3
4
5
6
7

0
0
0
0
0
0
0
0
0

0
1
0
0
1
0
0
1
0

1
0
1
1
0
1
1
0
1

1
1
1
1
1
1
0
1
1


Задание 4. Исследование логических схем (автоматический режим). На панели инструментов откройте Inctruments. Выберите Word Generator и Loqis Analyzer. Удалите из схемы (Рис.4) источник питания и переключатели. Замените их генератором слов Word Generator. Подключите к входам и выходам схемы анализатор логики Loqis Analyzer. В результате получите схему, приведенную на рис.5.




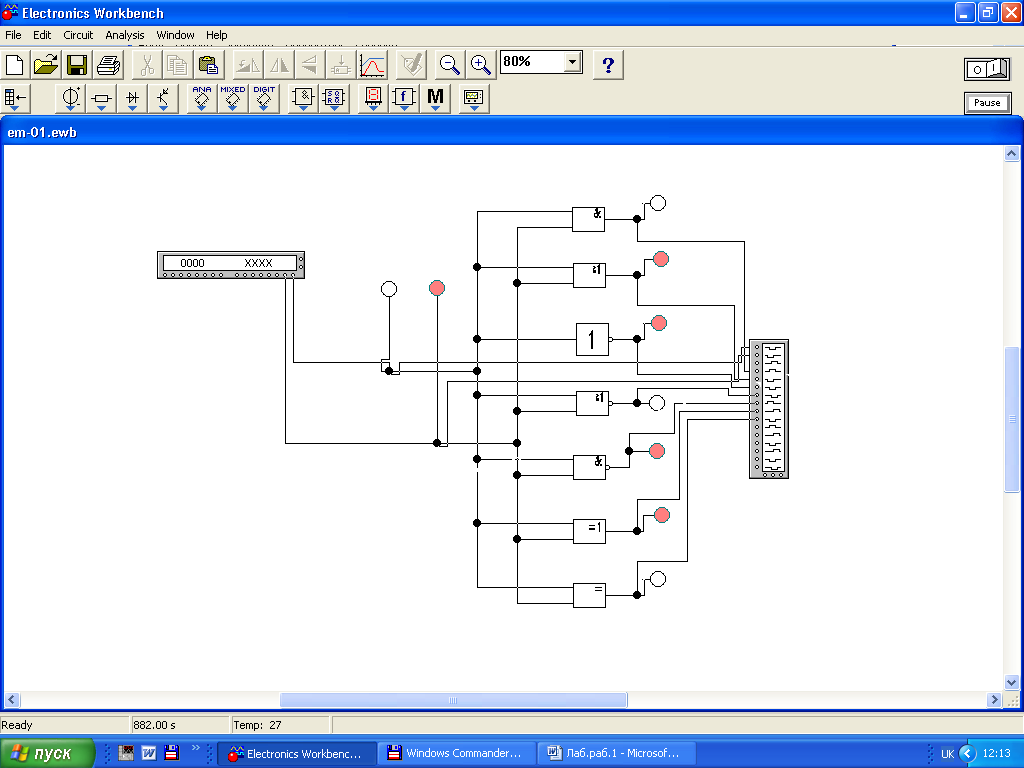
Рис.5
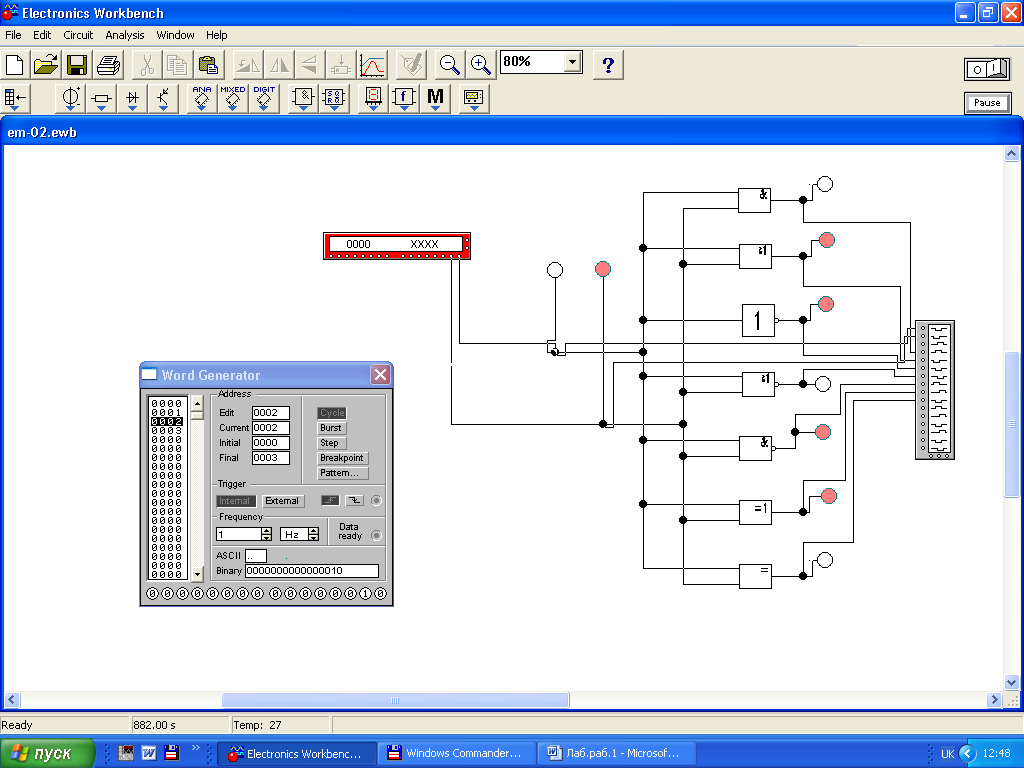
Отредактируйте четыре первых слова генератора слов в окне Binary, выставив в двоичной системе счисления соответственно 0 (….0000), 1 (….0001), 2 (….0010), 3 (….0011). Выставьте конечный адрес (Final) 0003. Установите частоту выдачи слов Frequency 1Hz (рис.6). Приведите в соответствие также частоту тактирования в Loqis Analyzer, выставив Internal clok rate в Clok setup также 1Hz. Включите моделирование. Зафиксируйте осциллограммы логических сигналов и дайте им интерпретацию.




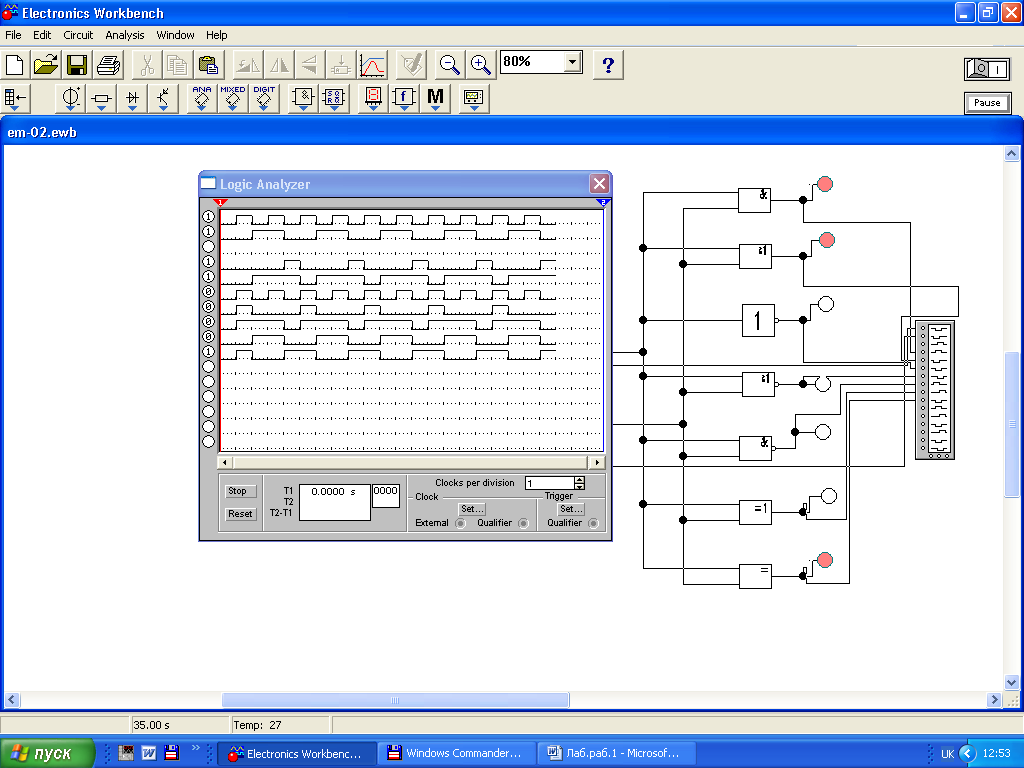
Вывод: в данной лабораторной работе исследовали базовую логику и определили реализуемые функции схемных решений. Также познакомились с принципом работы испытательного стенда для изучения устройств цифровой вычислительной техники.
Лабораторная работа № 3
Исследование интегральных триггеров
1. Цель работы

Изучение функционирования схем интегральных триггеров, овладение методами их проектирования, приобретения навыков исследования свойств триггеров с помощью персональных компьютеров.
2. Порядок выполнения лабораторной работы
Задание 1. Исследование асинхронного RS - триггера на элементах И-НЕ.

Открываем схему (файл ) асинхронного RS (Set-Reset)-триггера, построенного на логических элементах НЕ и И-НЕ (рис. 3.3). Составляем таблицу состояния на выходах триггера в зависимости от текущего и предыдущего состояния переключателей R и S. Дайте объяснение процессам, которые происходят в триггере. Приведите условное графическое изображение на схемах.

R
S
Q t
Q t+1

0
0
0
0

0
1
0
1

1
0
1
0

1
1
1
1


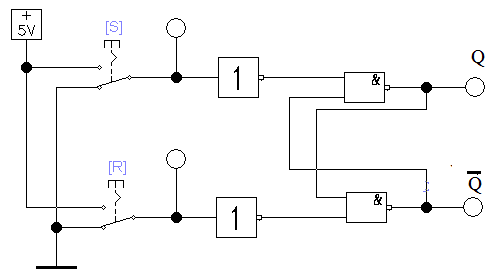
Рис. 3.3


Задание 2. Исследование асинхронного RS - триггера на элементах ИЛИ-НЕ.

Открываем схему (файл ) асинхронного RS-триггера, построенного на логических элементах НЕ и ИЛИ-НЕ (рис. 3.4). Составляем таблицу состояния на выходах триггера в зависимости от текущего и предыдущего состояния переключателей R и S. Даем объяснение процессам, которые происходят в триггере. Сравниваем работу этого триггера с работой триггера на логических элементах НЕ и И-НЕ.

R
S
Q t
Q t+1

0
0
0
0

0
1
0
1

1
0
0
1

1
1
1
1

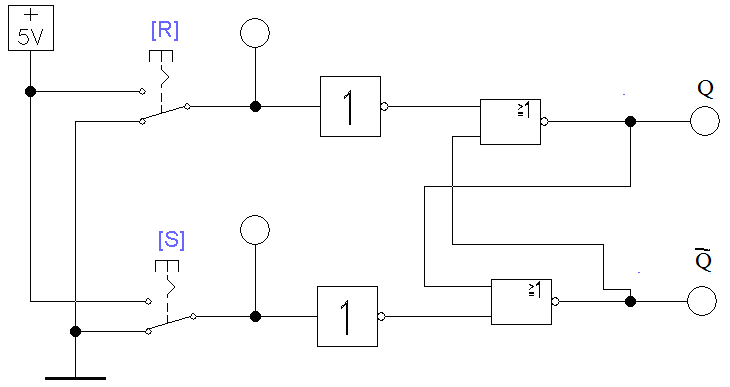
Рис. 3.4
Задание 3. Исследование синхронного RS - триггера на элементах И-НЕ.

Используя панель инструментов, дополняем схему рис. 3.3 логическими элементами И-НЕ и выключателями так, чтобы получить схему синхронного RS -триггера, представленного на рис. 3.5. Составляем таблицу состояния на выходах триггера в зависимости от текущего и предыдущего состояния переключателей 1,2, R, S и С. Даем объяснение процессам в триггере в виде временных диаграмм. Приведите условное графическое изображение на схемах.

С
R
S
Q t
Q t+1

0
0
0
0
0

1
0
1
0
1

1
1
0
1
0

1
1
1
1
1


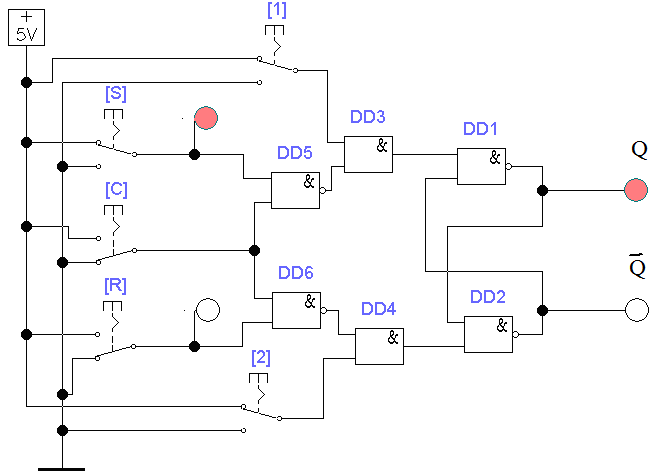
Рис. 3.5

Для упрощения изображения схемы триггера воспользуемся методикой построения субблоков. При нажатой левой кнопке мыши обведем все логические элементы схемы рис. 3.5, которые планируем включить в субблок. В меню откроем Circuit, выберем Create Subcircuit и нажмем на нем кнопку мыши. В окне pop-up меню Subcircuit напишем название субблока, например, RS_SUB. Удалим теперь часть схемы, которая вошла в субблок RS_SUB. На панели инструментов открываем Favorites, где должен находиться сформированный субблок RS_SUB. Забираем субблок и монтируем его в схему вместо удаленной части схемы. Должны получить схему, представленную на Рис. 3.6.



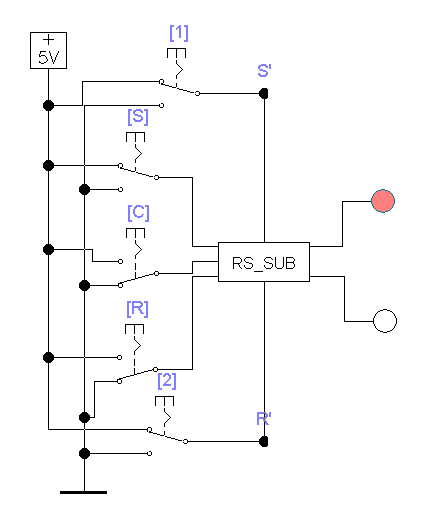
Рис. 3.6

После окончания монтажа схемы видим, что она работает так же, как и полная схема.
  1   2   3   4

Задание 4. Исследование двухступенчатого синхронного RS - триггера.

Синхронный двухступенчатый триггер со структурой "М-S" (Master-Slave) состоит из двух синхронных триггеров, где между основным (принимает новую входную информацию) и вспомогательным (передает старую информацию) включается инвертор, который блокирует перезапись информации во вспомогательный триггер при записи информации в основной триггер. Исполняем схему рис. 3.6 еще с одним схемным субблоком и сделаем соединения так, чтобы получить схему двухступенчатого синхронного RS-триггера, представленного на рис. 3.7.



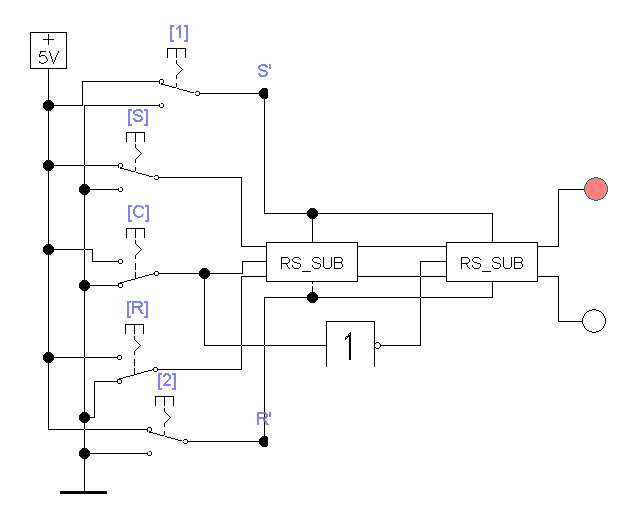
Рис. 3.7

Проводим анализ работы схемы. Появление сигнала на выходе двухступенчатого триггера задерживается на время действия тактового импульса.

Задание 5. Исследование D-триггера.

Состояние D-триггера повторяет значение сигнала на D-входе в тактовые моменты времени. Схему D-триггера можно построить на основе синхронного RS-триггера, если сигнал на вход S одновременно подавать через инвертор и на вход R. Дополним схему рис. 3.6 логическим элементом НЕ, как показано на рис. 3.8


D
C
Q t
Q t+1

0
0
0
0

1
0
0
1

1
1
1
1

0
1
0
1
.

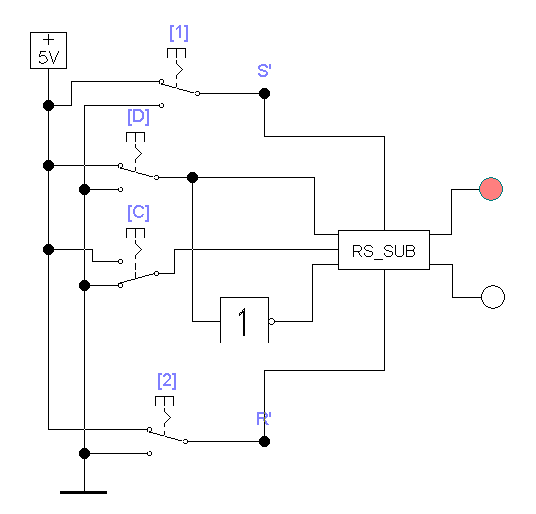
Рис. 3.8

Полученная схема, аналогична схеме показанной на рис. 3.9.



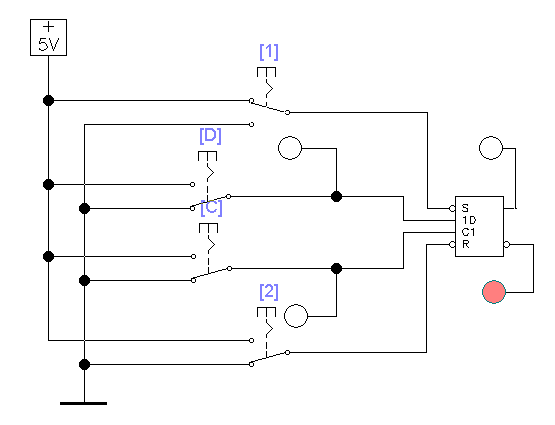
Рис. 3.9

Составляем таблицу состояния на выходах триггера в зависимости от текущего и предыдущего состояния переключателей 1,2,
D и С. Даем объяснение процессам в триггере в виде временных диаграмм.
Задание 6. Исследование Т-триггера.

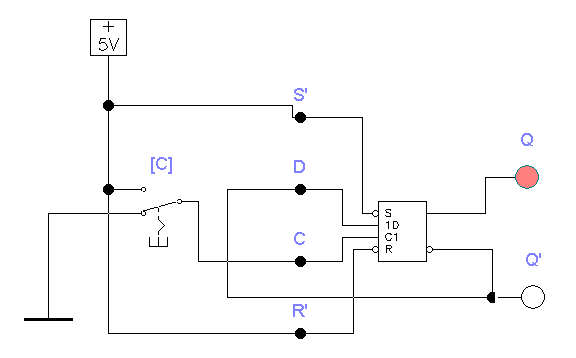
Открываем файл схемы модифицированного D-триггера (рис. 3. 10). Составляем таблицу состояния на выходах модифицированного D-триггера в зависимости от текущего и предыдущего состояния переключателя С. Даем объяснение процессам, которые происходят в триггере. Сравниваем работу этого триггера с работой предыдущей схеме.


Рис. 3.10
Частота выходных импульсов в 2 раза ниже частоты входных. Поэтому Т-триггеры используются как делители частоты на 2 или счетчики по модулю 2. В виде ИМС триггеры этого типа не выпускаются. Их можно легко создать на основе D- и JK-триггеров.
Задание 7. Исследование универсального JK - триггера.

Для исследования функционирования JK-триггера открываем файл (рис. 3.11). Промышленность выпускает готовые JK-триггеры на основе двухступенчатых синхронных RS-триггеров со структурой "М-S". Универсальный JK-триггер, кроме дополнительных установочных входов R и S имеет входы J, K и синхронизирующий вход С.


С
J
K
Q t
Q t+1

0
0
1
1
0

1
0
1
0
1

1
1
0
0
1

1
1
1
1
1

0
0
1
0
1

1
1
1
1
1


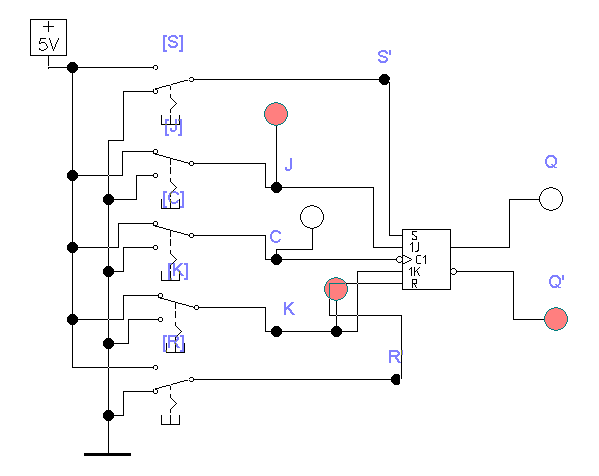
Рис. 3.11
При условии наличия нулевых сигналов на входах J, K, С триггер сохраняет свое состояние;

сигнал на входе J = 1 включает триггер в состояние логической «1» (Q = 1) по окончании тактового импульса С = 1;

сигнал на входе К = 1 сбрасывает триггер (Q = 0) по срезу тактового импульса С = 1;

при наличии сигналов J = К = 0 поступление тактового импульса не вызывает изменений в состоянии триггера;

Вывод: На базе JK-триггера можно создать: синхронный RS-триггер. Если принять, что J = S, К = R, а комбинацию J = К = 1 считать запрещенной. JK-триггер будет реагировать на изменение входных сигналов лишь в момент среза тактового импульса на входе С. Счетный Т-триггер. В этом триггере входы J и К соединяют между собой и подают на них напряжение логической единицы, так что J = К = 1, а вход С обозначают как Т. Тогда каждый тактовый импульс на входе синхронизации С = Т = 1 изменяет состояние триггера на противоположное. D-триггер. D-триггер может быть выполнен на базе JK-триггера включением на входах J, К элемента НЕ, который обеспечивает выполнение условий J = К '= D. В этом случае триггер запоминает сигнал на входе D в момент тактового импульса и держит его до следующего тактового импульса ("delay"-задержка). Поэтому D-триггер может использоваться как элемент памяти.

Лабораторная работа № 4
Исследование счетчиков
1. Цель работы

Изучение структуры и функционирования схемных разновидностей счетчиков, овладение методами их проектирования, приобретения навыков исследования с помощью персональных компьютеров.
3. Порядок выполнения лабораторной работы

Задание 1. Построить и исследовать схему трехразрядного двоичного суммирующего счетчика с последовательным переносом на D – триггерах.

Для построения схемы двоичного суммирующего счетчика руководствуются общими принципами их построения:

показания с двоичного счетчика снимаются с прямых выходов триггеров;

разряды двоичного счетчика строятся на двухступенчатых Т-триггерах или D-триггерах в счетном режиме;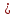

число разрядов n двоичного счетчика для заданного модуля М находят из выражения, 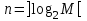где - знак округления до целого числа;

счетные импульсы асинхронного суммирующего счетчика поступают на Т - вход только первого (младшего) разряда;

сигналы переноса передаются асинхронно (последовательно во времени) с прямых выходов (для счетчиков на двухступенчатых Т - триггерах) и с инверсных выходов (для счетчиков на D - триггерах с динамическим управлением по фронту синхросигнала) соседних младших разрядов на Т - входы соседних старших;

изменение состояний триггеров в счетчиках на двухступенчатых Т-триггерах происходит по спаду (из 1 в 0), а в счетчиках на D - триггерах в счетном режиме - по фронту (из 0 в 1) входных импульсов.
Откройте файл (рис. 4.1).


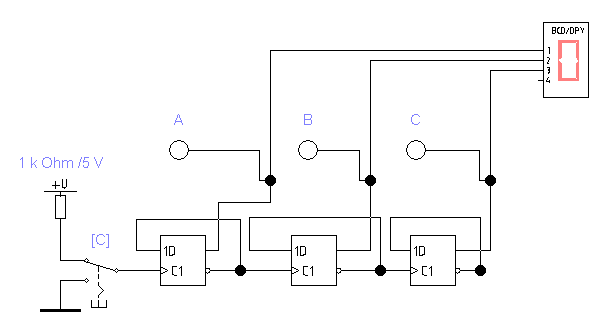
Рис. 4.1

Внимательно анализируем открытую схему. Включаем моделирование. Нажимая кнопку (выключатель) С, следим за состоянием светодиодов на выходах D - триггеров и по цифровому индикатору. Составьте таблицу состояний счетчика для серии последовательных тактов выключателя С, начиная со значения 0 цифрового индикатора. Чертим временную диаграмму работы счетчика.
Задание 2. Увеличьте разрядность счетчика до 4-х.

Для этого модернизируем схему асинхронного счетчика, добавив четвертый разряд так, как это показано на рис. 4.2.


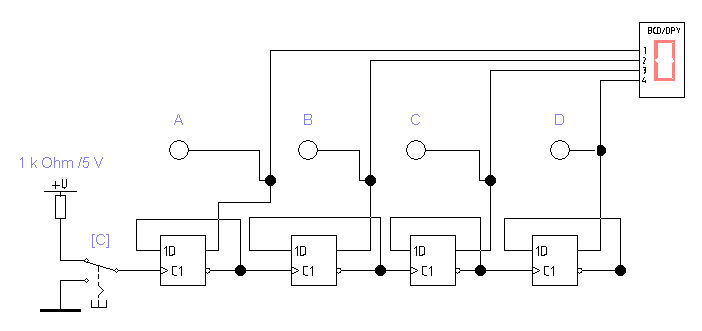
Рис. 4.2

Запускаем моделирование. Составляем таблицу состояний счетчика (табл. 1) для серии последовательных тактов, начиная со значения 0 цифрового индикатора. Дайте объяснение процессам в схеме рис. 4.2.

Таблица 1

№ пп
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

ЦИ16
1
0
0
0
0
1
1
1
0
0
0
0
1
1
1
1

А
1
0
0
0
1
0
0
0
1
1
1
1
0
0
0
0

В
0
1
0
0
1
0
0
0
1
1
1
0
0
0
0
1

С
1
1
0
0
1
0
0
0
1
0
1
1
1
1
1
0

D
0
0
0
0
1
1
1
1
0
1
0
0
0
0
0
1


Задание 3. Построить и исследовать схему трехразрядного двоичного вычитающего счетчика с последовательным переносом на D – триггерах.

В двоичном вычитающем счетчике каждый вычитающий импульс уменьшает состояние счетчика на единицу. Сигналы межразрядной связи называются займами. По правилу двоичного вычитания заем из старшего разряда с единичным значением возникает при условии, если все младшие триггеры находятся в нулевом состоянии. После этого все они переключаются в состояние "1", а старшие - в состояние "0".

Для создания вычитающих счетчиков чаще используют один из следующих способов:

в приведенных суммирующих счетчиках информацию снимать не с прямых, а с инверсных выходов триггеров;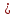

сигналы займа снимаются с инверсных выходов двухступенчатых Т - триггеров или с прямых выходов D - триггеров в счетном режиме.

Число, соответствующее значению кода на прямых выходах триггера счетчика (NПР), связано с числом, которое соответствует значению кода на инверсных выходах (NИНВ) триггеров, следующим выражением:

.

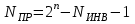В таблице 2 приведен пример связи числа NПР с числом NИНВ трехразрядного двоичного счетчика.

Таблица 2

Состояние прямых выходов
Число
Состояние инверсных выходов
Число

Q3
Q2
Q1
NПР
Q3’
Q2’
Q1’
NИНВ

0
0
0
0
1
1
1
7

0
0
1
1
1
1
0
6

0
1
0
2
1
0
1
5


Открываем файл (рис. 4.3) и анализируем работу схемы.


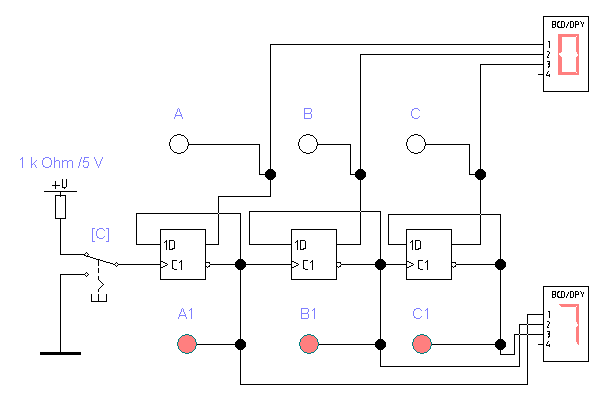
Рис. 4.3
1   2   3   4

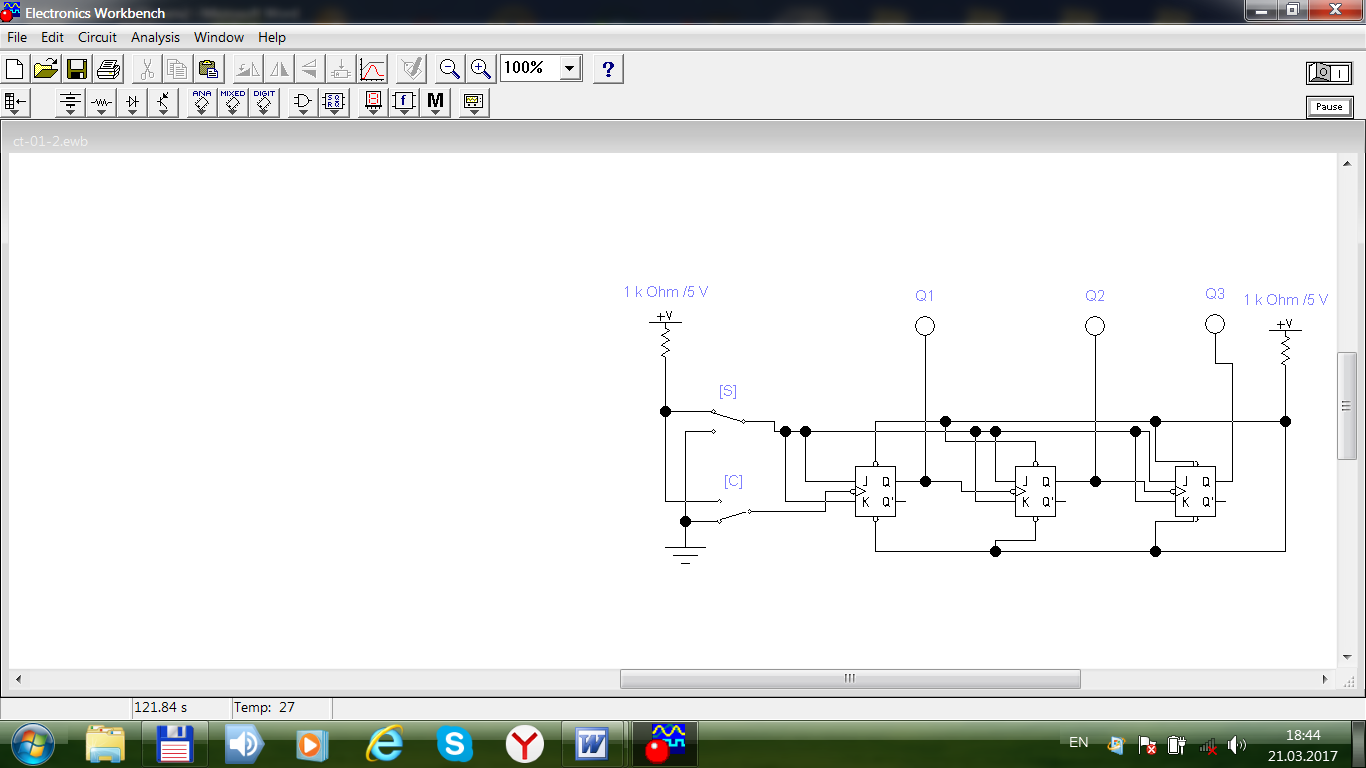
Задание 4. Открываем файл (рис. 4.4) и сравните открытую Вами схему с ранее рассмотренными. Проведите моделирование.


Рис. 4.4
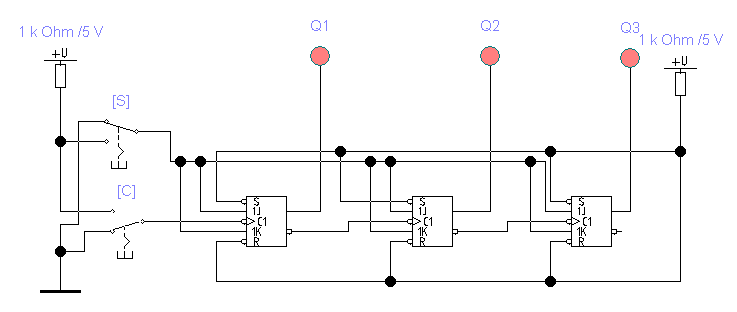
Задание 5. Открываем файл (рис. 4.5). Проведите анализ схемы и моделирование.

Рис. 4.5

Рассмотренные двоичные счетчики с последовательным переносом относительно просты по схеме, но имеют низкое быстродействие, так как во время его работы требуется последовательное переключение всех n триггеров.

Наибольшим быстродействием обладают счетчики с параллельным переносом. Для этого в каждом разряде синхронного счетчика появляется схема совпадения, с помощью которой анализируются состояния всех предыдущих младших триггеров и производится функции переноса согласно таким логическими соотношениями:



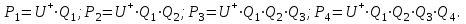
При поступлении очередного счетного импульса U+ переключаются только те триггеры, для которых все предыдущие (младшие) разряды находятся в этот момент в единичном состоянии.

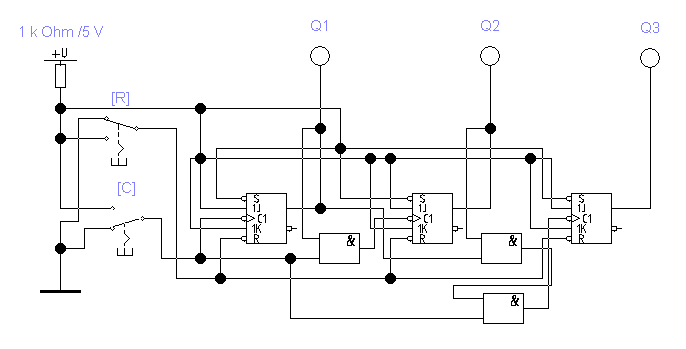
Задание 6. Откройте файл (рис. 4.6). Проведите анализ схемы и моделирование. Дайте объяснение процессам в схеме.


Рис. 4.6

Задание 7. Построить и исследовать схему трехразрядного двоичного реверсивного счетчика с последовательным переносом на D – триггерах.

Реверсивные счетчики выполняют подсчет сигналов, как в режиме прямого счета (сложения), так и в обратном режиме (вычитания). Режим работы меняется с помощью схемы управления. В зависимости от требований к схеме управления можно построить реверсивные счетчики двух типов:

с одним счетным и одним управляющим входом;

Смотрите также файлы