Файл: Герасимов Виктор Олегович Проверил преподаватель Сватов В. Ф. Тюмень Тиу 2023 лабораторная работа 1 Синтез и исследование.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 45
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с двумя счетными входами.
Для реверсирования счета в таких схемах необходимы дополнительные логические элементы 2-2И-ИЛИ ("схемы реверса"), которые выполняют коммутацию выходов триггеров счетчика.
Для счетчиков первого типа, эта коммутация выполняется с помощью сигнала управления V, который принимает значения 1 или 0 в зависимости от заданного направления счета. С учетом этого можно записать функции возбуждения триггеров для счетчиков с последовательным переносом в виде:
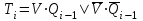
Откройте файл (рис. 4.7) и проанализируйте схему. Запустите моделирование и убедитесь, что схема работает корректно.
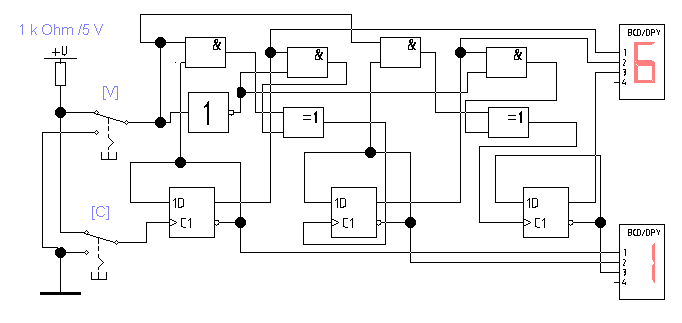
Рис. 4.7
Если, сигнал V = 1, то счетчик реализует режим суммирования, в противном случае (V = 0) - обеспечивает режим вычитания.
При построении реверсивных счетчиков с двумя счетными входами необходимо учесть, что в режиме суммирования входные импульсы поступают на счетный вход Х, а в режиме вычитания - на Y, причем для нормального функционирования счетчика эти сигналы не должны поступать одновременно.
Функции возбуждения триггеров для счетчиков с последовательным переносом будут иметь следующее выражение:
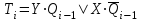
Примером счетчика с двумя счетными входами есть цифровая ИМС К555ИЕ6 или К555ИЕ7.
Задание 8. Построить и исследовать двоичный счетчик с произвольным модулем счета.
Счетчики с произвольным модулем счета, реализуются на основе нескольких методов. Принцип их построения состоит в исключении некоторых устойчивых состояний обычного двоичного счетчика. Эти состояния исключаются с помощью обратных связей внутри счетчика, образующиеся введением дополнительных логических цепей, соединяющих входы и выходы соответствующих триггеров.
Задача синтеза таких счетчиков сводится к определению необходимых обратных связей и минимизации их числа.
Число лишних состояний L определяется соотношением:
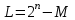
где: n - разрядность счетчика;
М - заданный модуль счета.
В общем случае выбор состояний, которые исключаются, определяется назначением счетчика. В зависимости от того, какие состояния исключаются, различают:
счетчики с нулевым начальным состоянием и естественным порядком счета;
счетчики с начальной установкой кода и естественным порядком счета;
счетчики с произвольным порядком счета.
Примеры графов функционирования всех трех типов счетчиков для случая n = 3 и М = 5 показаны на рис. 4.8.
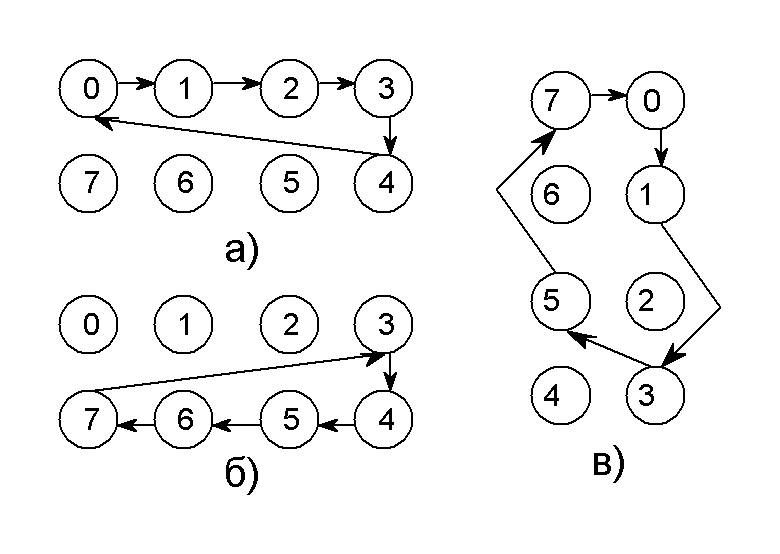
Рис. 4.8
Из рис. 4.8,а очевидно, что счетчик считает до кодового состояния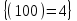
и после его достижения сбрасывается до нуля.
Факт попадания счетчика в нерабочее состояние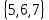
описывается логическим выражением:
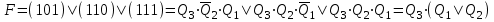Факт появления нерабочего состояния (F=1) счетчика должен фиксироваться логической схемой.
Реализуем логическую функцию на элементах И-НЕ. Для этого выражение функции запишем в виде: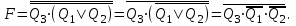
Откройте (рис. 4.9) и проанализируйте схему.
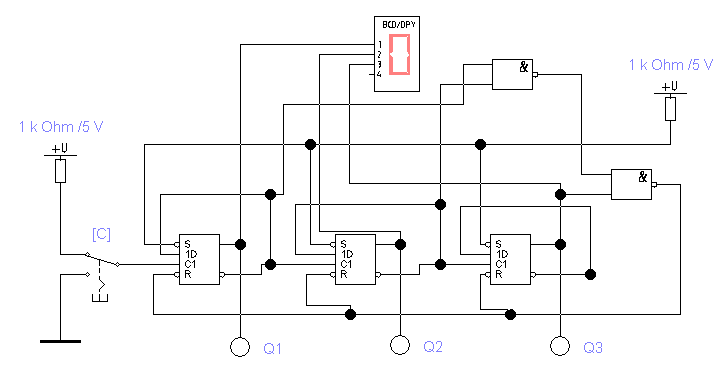
Рис. 4.9
Запускаем моделирование и убеждаемся, что схема работает правильно и обеспечивает коэффициент счета (деления) равным 5.
Вывод: по правилу двоичного вычитания заем из старшего разряда с единичным значением возникает при условии, если все младшие триггеры находятся в нулевом состоянии.
Наибольшим быстродействием обладают счетчики с параллельным переносом. Для этого в каждом разряде синхронного счетчика появляется схема совпадения, с помощью которой анализируются состояния всех предыдущих младших триггеров и производится функции переноса согласно таким логическими соотношениями.
Лабораторная работа № 5
Исследование регистров памяти
1. Цель работы
Ознакомиться с принципами построения и работы регистров памяти, провести исследование схем регистров, приобрести навыки схемотехнического моделирования на персональных компьютерах.
Задание_1.'>2. Порядок выполнения работы
Задание 1. Построить и исследовать последовательный регистр сдвига на D-триггерах.
Последовательный регистр сдвига имеет один информационный вход D, вход синхронизации С, вход сброса R и один информационный выход Q.
В таких схемах регистров:
целесообразно использовать синхронные двухступенчатые D -триггеры с однофазным приемом информации, имеющие динамические С -входы и независимые установочные входы R и S;
входы С всех триггеров объединяют и подключают к общей шине, на которую подаются импульсы сдвига;
прямой выход предыдущего триггера соединяется с D - входом следующего.
Схема представляет собой четырехразрядный регистр из последовательно включенных D - триггеров. На выходе каждого триггера установлен индикатор логического уровня.
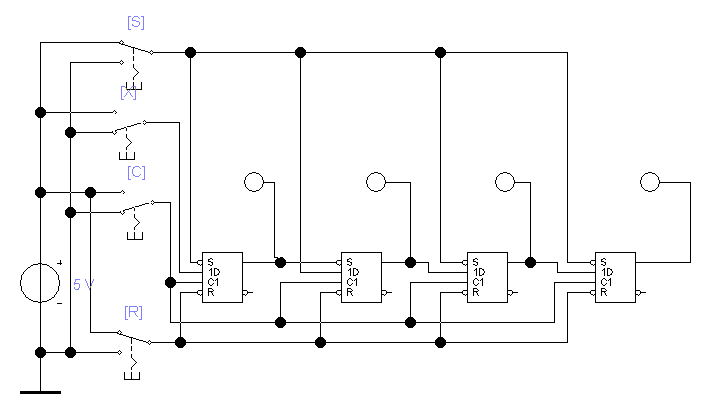
Рис. 5.1
В этом регистре ввод информации производится с входа Х с последующим смещением вправо на один разряд по каждому синхроимпульсу С. По положительному фронту синхроимпульса С = 1 осуществляется запись информации со входов D в триггеры первых ступеней. Выходные уровни триггеров при этом остаются неизменными. По отрицательному фронту синхроимпульса С = 1 входы D-триггеров первой ступени блокируются и записанная в них информация передается в триггеры второй ступени. Возникает переключение выходных уровней D-триггеров. Каждый разряд регистра одновременно принимает информацию из предыдущего разряда и передает информации в последующий. Таким образом, схема на рис. 5.1 представляет собой чисто последовательный регистр со сдвигом числа вправо (вход - Х, выход - Q).
Задание 2. Построить и исследовать параллельно-последовательный регистр сдвига на D-триггерах.
Параллельно-последовательный регистр сдвига имеет n входов для параллельной записи информации (D1, D2, D3, ...), вход синхронизации С, специальный вход управления V и один выход Q.
Регистр имеет 2 режима работы:
1. Режим параллельной записи - когда сигнал V = 1. В этом режиме по синхроимпульсу на входе С, информация из n входов Х1
, Х2, ... Хn записывается в триггеры D1, D2, D3, ....
2. Режим сдвига - когда сигнал V = 0. Это позволяет по каждому синхроимпульсов на входе С, информации, которая была ранее установлена в регистре с записью в D1, D2, D3, ... поочередно поступает на выход Q.
Модернизируем схему рис. 5.1. Для ввода информации в регистр сигналом V = 1 из n входов Х1, Х2, ... Хn необходимо дополнить схему двухвходовыми логическими элементами И на входе, которые формируют входные сигналы согласно выражению: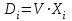
. Если на некотором i-м входе Хi = 1, то Di = 1 и i-й триггер переключается в состояние "1" и наоборот - когда на входе Хi = 0, то и i-й триггер переключается в состояние "0".
Откройте файл, появится схема, изображенная на рис. 5.2.
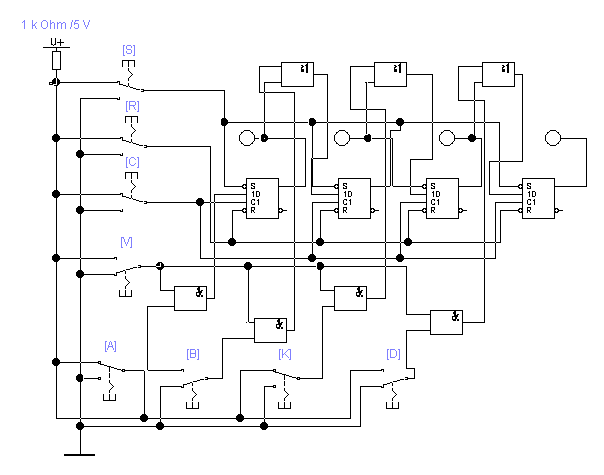
Рис. 5.2
Включаем моделирование. Очищаем регистр нажатием клавиши R. Управляющим сигналом V = 1 вводим произвольное двоичное число Хi в регистр (нажатием на клавиши А, В, К, D). Сигналом V = 0 и двойным нажатием на клавишу С можно продвигаем введенную информации по регистру.
При замыкании выхода последнего разряда через логический элемент ИЛИ со входом D младшего разряда можно реализовать кольцевой регистр сдвига. Открываем файл, появится схема, изображенная на рис. 5.3. Анализируем схему и убедитесь в работе кольцевого регистра.
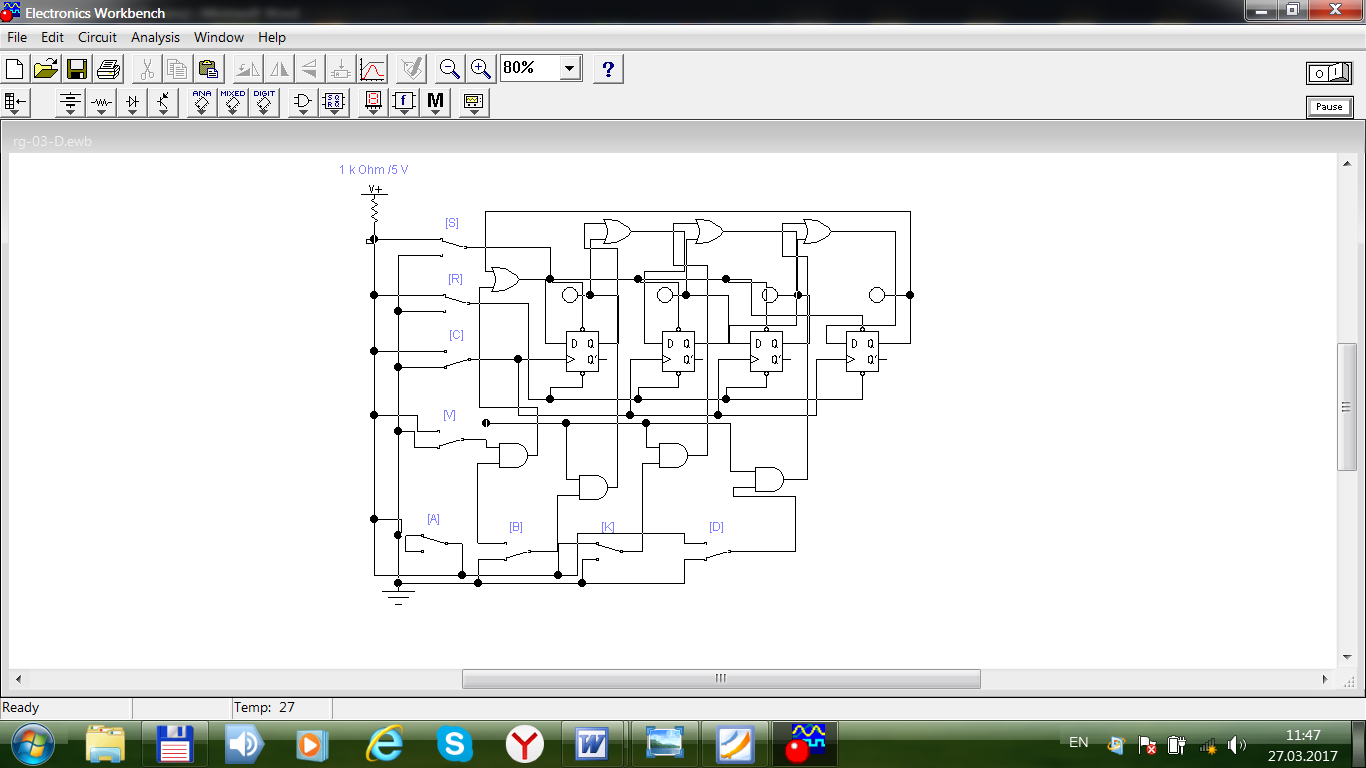
Рис.5.3
При синтезе регистра со сдвигом в сторону младших разрядов, выполняем объединение (через логический элемент ИЛИ) прямых выходов каждого последующего разряда регистра с входом параллельной записи предыдущего разряда, то есть реализовать выражение: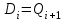
. Открываем файл появится схема рис. 5.4.
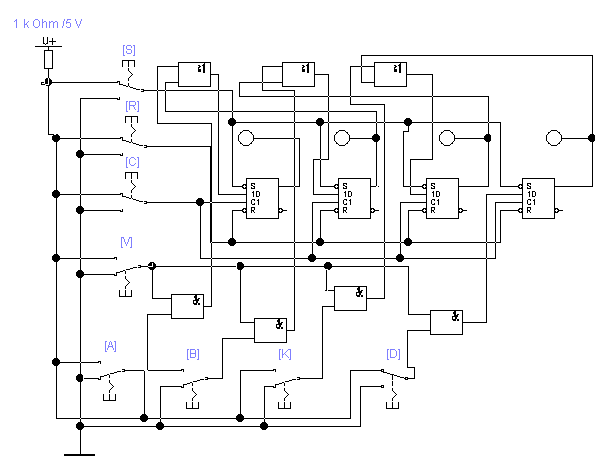
Рис. 5.4
Для построения кольцевых регистров сдвига удобно и использовать JK - триггеры. Открываем файл, появится схема, изображенная на рис. 5.5.
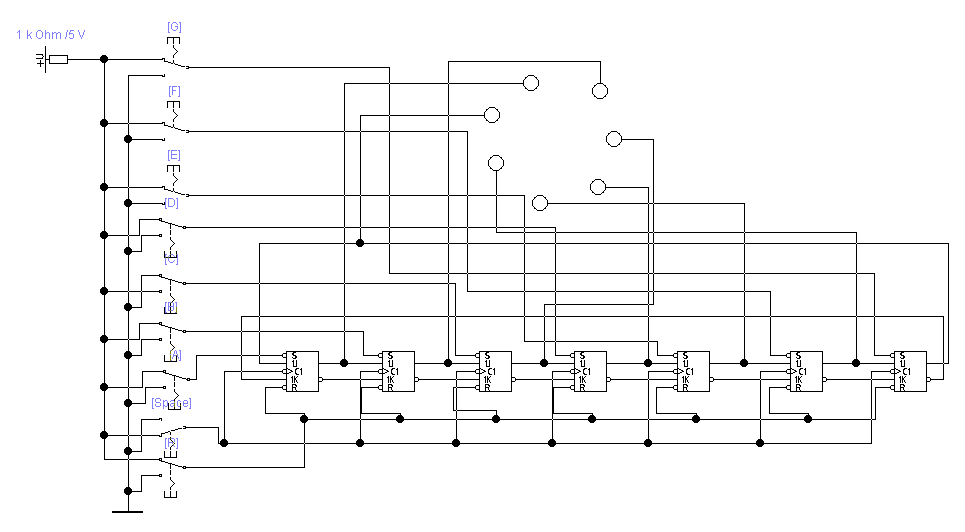
Рис. 5.5
Включите моделирование и проанализируйте работу схему.
Задание_3.'>Задание 3. Построить и исследовать реверсивный регистр сдвига на D-триггерах.
В реверсивных сдвиговых регистрах, для обеспечения возможности смещения информации в обоих направлениях, выход каждого разряда должен быть связан через логические элементы переключения направления сдвига с входами предварительного и последующего разрядов. Исходя из этого, получим логическое уравнение, описывающее работу схемы управления при использовании D-триггеров: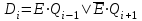
.
Откройте файл, появится схема реверсивного регистра сдвига на D – триггерах, которая изображена на рис. 5.6.
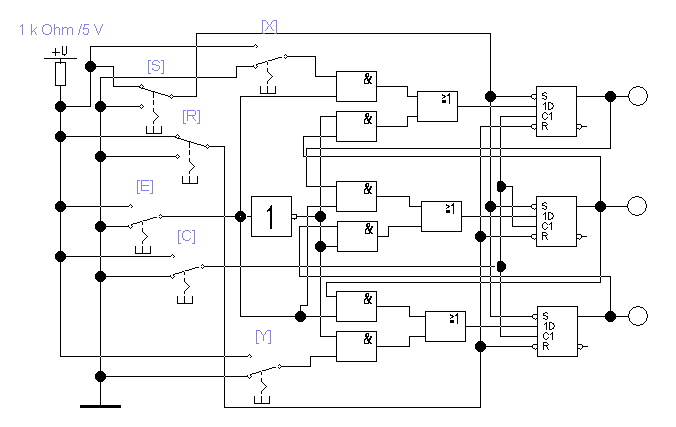
Рис. 5.6
Схема трехразрядного регистра имеет тактовый вход С, вход установки в нулевое состояние R, два входа для последовательного приема информации X при сдвиге в сторону старших разрядов и Y - при сдвиге в сторону младших разрядов, управляющей вход Е для выбора направления сдвига.
Включаем моделирование и анализируем работу схемы.
Задание 4. Модернизируйте схему реверсивного регистра сдвига на D-триггерах для параллельного приема информации.
Открываем файл, появится схема реверсивного регистра сдвига на D - триггерах с параллельным приемом информации.
Включаем моделирование.
Вывод: С приходом очередного тактового импульса происходит перезапись (сдвиг) содержимого триггера каждого разряда в соседний разряд (от разряда А к разряду D) без изменения порядка следования единиц и нулей.
Лабораторная работа № 6
Исследование шифраторов и дешифраторов
1. Цель работы
Ознакомиться с принципами построения и функционирования шифраторов и дешифраторов, провести исследование этих схем, приобрести навыки схемотехнического моделирования на персональных компьютерах.
2. Порядок выполнения работы
Задание 1. Построить и исследовать полный шифратор, преобразующий трехразрядный распределительный код в двоичный позиционный.
Последовательность синтеза схемы шифратора такова:
составить таблицу истинности, которая отражают логику функционирования шифратора;
из таблицы истинности получить логические выражения выходных функций шифратора в дизъюнктивной или конъюнктивной форме;
с помощью логических элементов реализовать логические функции и построить схему полного шифратора.
Открываем один из файлов от до . Сравниваем открытую схему шифратора со схемой, изображенной на рис. 6.3. Исправьте ошибки.
Включаем моделирование. Поочередно нажимая (каждую отдельно) клавиши 1-7, следим за состоянием светодиодов на входе и выходе схемы и за показаниями цифрового индикатора. Составляем таблицу истинности (табл. 1).
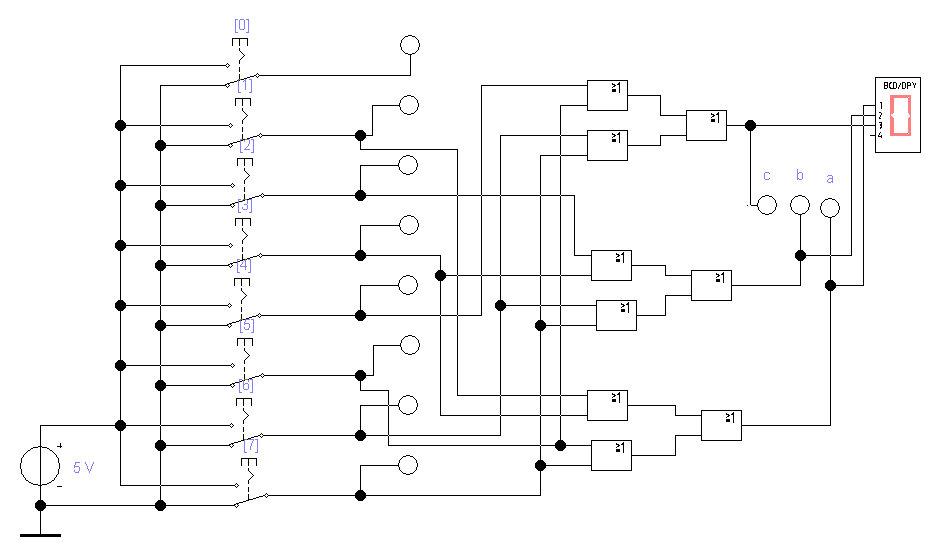
Рис. 6.3
Анализируя схему, можно обобщить принципы построения шифраторов для многоразрядных распределительных кодов. на входы каждого элемента ИЛИ подключаются разряды распределительного кода с номерами, запись которых в двоичном позиционном коде требует выработки на выходе элемента ИЛИ единичного значения двоичного разряда. К особенности построения схемы шифраторов на элементах И-НЕ необходимо отнести то, что на их вход необходимо подавать инверсный распределительный код.
Задание 2. Построить и исследовать приоритетный шифратор 4 2.
Шифраторы, которые при одновременном нажатии нескольких клавиш производят код только старшей цифры, называют приоритетными.
В таблице истинности приоритетного шифратора 4 2 (табл.. 3) все старшие нули и старшая единица входных переменных определяют исходный код, а значения входных переменных справа от диагонали, образованной цифрами 1, не определяют исходный код - обозначены крестиком.
Таблица 3
Из табл. 3 получаем выражения для логических функций Y0, Y1 в виде совершенной дизъюнктивной нормальной форме (СДНФ), как суммы минтермов (произведений входных переменных) единичных наборов. При этом будем игнорировать входные переменные, которые не определяют исходный код, а для упрощения выражений используем тождество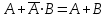
и законы де Моргана:
; 
.
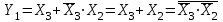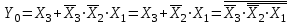Согласно полученным выражениям построим схемы приоритетного шифратора 4 2 в базисах И, ИЛИ, НЕ и И-НЕ.
Открываем один из файлов от <cd-01-vl.ewb> до <cd-01-v7.ewb>. Проводим анализ схемы шифратора и исправьте ошибки. Включаем моделирование.
Задание 3. Построить и исследовать полный дешифратор 3 8, превращающий трех разрядный двоичный код в распределительный код.
Последовательность синтеза схемы дешифратора аналогична синтезу схем шифраторов:
составим таблицу истинности дешифратора и получим логические выражения выходных функций дешифратора в дизъюнктивной (при реализации в базисе И-НЕ) или конъюнктивной форме (при реализации в базисе ИЛИ-НЕ).
Логика работы полного дешифратора 3 8 приведена в таблице 4.
Таблица 4
Для реверсирования счета в таких схемах необходимы дополнительные логические элементы 2-2И-ИЛИ ("схемы реверса"), которые выполняют коммутацию выходов триггеров счетчика.
Для счетчиков первого типа, эта коммутация выполняется с помощью сигнала управления V, который принимает значения 1 или 0 в зависимости от заданного направления счета. С учетом этого можно записать функции возбуждения триггеров для счетчиков с последовательным переносом в виде:
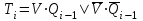
Откройте файл
Рис. 4.7
Если, сигнал V = 1, то счетчик реализует режим суммирования, в противном случае (V = 0) - обеспечивает режим вычитания.
При построении реверсивных счетчиков с двумя счетными входами необходимо учесть, что в режиме суммирования входные импульсы поступают на счетный вход Х, а в режиме вычитания - на Y, причем для нормального функционирования счетчика эти сигналы не должны поступать одновременно.
Функции возбуждения триггеров для счетчиков с последовательным переносом будут иметь следующее выражение:
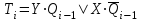
Примером счетчика с двумя счетными входами есть цифровая ИМС К555ИЕ6 или К555ИЕ7.
Задание 8. Построить и исследовать двоичный счетчик с произвольным модулем счета.
Счетчики с произвольным модулем счета, реализуются на основе нескольких методов. Принцип их построения состоит в исключении некоторых устойчивых состояний обычного двоичного счетчика. Эти состояния исключаются с помощью обратных связей внутри счетчика, образующиеся введением дополнительных логических цепей, соединяющих входы и выходы соответствующих триггеров.
Задача синтеза таких счетчиков сводится к определению необходимых обратных связей и минимизации их числа.
Число лишних состояний L определяется соотношением:
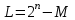
где: n - разрядность счетчика;
М - заданный модуль счета.
В общем случае выбор состояний, которые исключаются, определяется назначением счетчика. В зависимости от того, какие состояния исключаются, различают:
счетчики с нулевым начальным состоянием и естественным порядком счета;
счетчики с начальной установкой кода и естественным порядком счета;
счетчики с произвольным порядком счета.
Примеры графов функционирования всех трех типов счетчиков для случая n = 3 и М = 5 показаны на рис. 4.8.
Рис. 4.8
Из рис. 4.8,а очевидно, что счетчик считает до кодового состояния
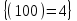и после его достижения сбрасывается до нуля. Факт попадания счетчика в нерабочее состояние
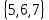описывается логическим выражением: 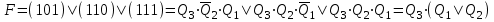Факт появления нерабочего состояния (F=1) счетчика должен фиксироваться логической схемой.Реализуем логическую функцию на элементах И-НЕ. Для этого выражение функции запишем в виде:
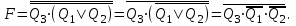
Откройте
Рис. 4.9
Запускаем моделирование и убеждаемся, что схема работает правильно и обеспечивает коэффициент счета (деления) равным 5.
Вывод: по правилу двоичного вычитания заем из старшего разряда с единичным значением возникает при условии, если все младшие триггеры находятся в нулевом состоянии.
Наибольшим быстродействием обладают счетчики с параллельным переносом. Для этого в каждом разряде синхронного счетчика появляется схема совпадения, с помощью которой анализируются состояния всех предыдущих младших триггеров и производится функции переноса согласно таким логическими соотношениями.
Лабораторная работа № 5
Исследование регистров памяти
1. Цель работы
Ознакомиться с принципами построения и работы регистров памяти, провести исследование схем регистров, приобрести навыки схемотехнического моделирования на персональных компьютерах.
Задание_1.'>2. Порядок выполнения работы
Задание 1. Построить и исследовать последовательный регистр сдвига на D-триггерах.
Последовательный регистр сдвига имеет один информационный вход D, вход синхронизации С, вход сброса R и один информационный выход Q.
В таких схемах регистров:
целесообразно использовать синхронные двухступенчатые D -триггеры с однофазным приемом информации, имеющие динамические С -входы и независимые установочные входы R и S; входы С всех триггеров объединяют и подключают к общей шине, на которую подаются импульсы сдвига; прямой выход предыдущего триггера соединяется с D - входом следующего. Схема представляет собой четырехразрядный регистр из последовательно включенных D - триггеров. На выходе каждого триггера установлен индикатор логического уровня.
Рис. 5.1
В этом регистре ввод информации производится с входа Х с последующим смещением вправо на один разряд по каждому синхроимпульсу С. По положительному фронту синхроимпульса С = 1 осуществляется запись информации со входов D в триггеры первых ступеней. Выходные уровни триггеров при этом остаются неизменными. По отрицательному фронту синхроимпульса С = 1 входы D-триггеров первой ступени блокируются и записанная в них информация передается в триггеры второй ступени. Возникает переключение выходных уровней D-триггеров. Каждый разряд регистра одновременно принимает информацию из предыдущего разряда и передает информации в последующий. Таким образом, схема на рис. 5.1 представляет собой чисто последовательный регистр со сдвигом числа вправо (вход - Х, выход - Q).
Задание 2. Построить и исследовать параллельно-последовательный регистр сдвига на D-триггерах.
Параллельно-последовательный регистр сдвига имеет n входов для параллельной записи информации (D1, D2, D3, ...), вход синхронизации С, специальный вход управления V и один выход Q.
Регистр имеет 2 режима работы:
1. Режим параллельной записи - когда сигнал V = 1. В этом режиме по синхроимпульсу на входе С, информация из n входов Х1
, Х2, ... Хn записывается в триггеры D1, D2, D3, ....
2. Режим сдвига - когда сигнал V = 0. Это позволяет по каждому синхроимпульсов на входе С, информации, которая была ранее установлена в регистре с записью в D1, D2, D3, ... поочередно поступает на выход Q.
Модернизируем схему рис. 5.1. Для ввода информации в регистр сигналом V = 1 из n входов Х1, Х2, ... Хn необходимо дополнить схему двухвходовыми логическими элементами И на входе, которые формируют входные сигналы согласно выражению:
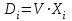. Если на некотором i-м входе Хi = 1, то Di = 1 и i-й триггер переключается в состояние "1" и наоборот - когда на входе Хi = 0, то и i-й триггер переключается в состояние "0".Откройте файл
Рис. 5.2
Включаем моделирование. Очищаем регистр нажатием клавиши R. Управляющим сигналом V = 1 вводим произвольное двоичное число Хi в регистр (нажатием на клавиши А, В, К, D). Сигналом V = 0 и двойным нажатием на клавишу С можно продвигаем введенную информации по регистру.
При замыкании выхода последнего разряда через логический элемент ИЛИ со входом D младшего разряда можно реализовать кольцевой регистр сдвига. Открываем файл
Рис.5.3
При синтезе регистра со сдвигом в сторону младших разрядов, выполняем объединение (через логический элемент ИЛИ) прямых выходов каждого последующего разряда регистра с входом параллельной записи предыдущего разряда, то есть реализовать выражение:
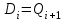. Открываем файл Рис. 5.4
Для построения кольцевых регистров сдвига удобно и использовать JK - триггеры. Открываем файл
Рис. 5.5
Включите моделирование и проанализируйте работу схему.
Задание_3.'>Задание 3. Построить и исследовать реверсивный регистр сдвига на D-триггерах.
В реверсивных сдвиговых регистрах, для обеспечения возможности смещения информации в обоих направлениях, выход каждого разряда должен быть связан через логические элементы переключения направления сдвига с входами предварительного и последующего разрядов. Исходя из этого, получим логическое уравнение, описывающее работу схемы управления при использовании D-триггеров:
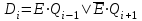.Откройте файл
Рис. 5.6
Схема трехразрядного регистра имеет тактовый вход С, вход установки в нулевое состояние R, два входа для последовательного приема информации X при сдвиге в сторону старших разрядов и Y - при сдвиге в сторону младших разрядов, управляющей вход Е для выбора направления сдвига.
Включаем моделирование и анализируем работу схемы.
Задание 4. Модернизируйте схему реверсивного регистра сдвига на D-триггерах для параллельного приема информации.
Открываем файл
Включаем моделирование.
Вывод: С приходом очередного тактового импульса происходит перезапись (сдвиг) содержимого триггера каждого разряда в соседний разряд (от разряда А к разряду D) без изменения порядка следования единиц и нулей.
Лабораторная работа № 6
Исследование шифраторов и дешифраторов
1. Цель работы
Ознакомиться с принципами построения и функционирования шифраторов и дешифраторов, провести исследование этих схем, приобрести навыки схемотехнического моделирования на персональных компьютерах.
2. Порядок выполнения работы
Задание 1. Построить и исследовать полный шифратор, преобразующий трехразрядный распределительный код в двоичный позиционный.
Последовательность синтеза схемы шифратора такова:
составить таблицу истинности, которая отражают логику функционирования шифратора; из таблицы истинности получить логические выражения выходных функций шифратора в дизъюнктивной или конъюнктивной форме; с помощью логических элементов реализовать логические функции и построить схему полного шифратора.Открываем один из файлов от
Включаем моделирование. Поочередно нажимая (каждую отдельно) клавиши 1-7, следим за состоянием светодиодов на входе и выходе схемы и за показаниями цифрового индикатора. Составляем таблицу истинности (табл. 1).
Рис. 6.3
Анализируя схему, можно обобщить принципы построения шифраторов для многоразрядных распределительных кодов. на входы каждого элемента ИЛИ подключаются разряды распределительного кода с номерами, запись которых в двоичном позиционном коде требует выработки на выходе элемента ИЛИ единичного значения двоичного разряда. К особенности построения схемы шифраторов на элементах И-НЕ необходимо отнести то, что на их вход необходимо подавать инверсный распределительный код.
Задание 2. Построить и исследовать приоритетный шифратор 4
2.Шифраторы, которые при одновременном нажатии нескольких клавиш производят код только старшей цифры, называют приоритетными.
В таблице истинности приоритетного шифратора 4
2 (табл.. 3) все старшие нули и старшая единица входных переменных определяют исходный код, а значения входных переменных справа от диагонали, образованной цифрами 1, не определяют исходный код - обозначены крестиком.Таблица 3
| № набора | Входы | Выходы | ||||
| Х3 | Х2 | Х1 | Х0 | Y1 | Y0 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | | 0 | 1 |
| 2 | 0 | 1 | | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 |
Из табл. 3 получаем выражения для логических функций Y0, Y1 в виде совершенной дизъюнктивной нормальной форме (СДНФ), как суммы минтермов (произведений входных переменных) единичных наборов. При этом будем игнорировать входные переменные, которые не определяют исходный код, а для упрощения выражений используем тождество
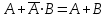и законы де Моргана: 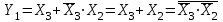; 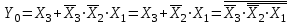.Согласно полученным выражениям построим схемы приоритетного шифратора 4
2 в базисах И, ИЛИ, НЕ и И-НЕ.Открываем один из файлов от <cd-01-vl.ewb> до <cd-01-v7.ewb>. Проводим анализ схемы шифратора и исправьте ошибки. Включаем моделирование.
1 2 3 4
Задание 3. Построить и исследовать полный дешифратор 3
8, превращающий трех разрядный двоичный код в распределительный код.Последовательность синтеза схемы дешифратора аналогична синтезу схем шифраторов:
составим таблицу истинности дешифратора и получим логические выражения выходных функций дешифратора в дизъюнктивной (при реализации в базисе И-НЕ) или конъюнктивной форме (при реализации в базисе ИЛИ-НЕ).Логика работы полного дешифратора 3
8 приведена в таблице 4.Таблица 4
| Х3 | Х2 | Х1 | Y0 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |