2 Технология расчетной оценки сопротивления усталости и долговечности несущих узлов подвижного состава

2.1 Общие предпосылки

В настоящее время существуют программные средства, позволяющие решать задачи по оценке запаса сопротивления усталости и долговечности несущих узлов различных технических объектов. Эти средства требуют знания большого объема статистической информации, которую получают в результате дорогих экспериментальных исследований. Проведение их затруднительно. Поэтому не потеряло актуальность направление, связанное с поиском путей разработки оценочных методов расчета этих показателей, не требующих больших затрат и использующих минимальное число доступных исходных данных.

В предлагаемом разделе работы сформированы такие расчетные средства применительно к узлам подвижного состава железных дорог.

Естественно, что запасы сопротивления усталости и долговечности зависят, в первую очередь, от нагрузок, которые испытывают несущие узлы. Кроме нагрузок, важную роль играют механические свойства материалов, из которых изготовлены узлы, геометрия узлов, технология и качество их изготовления.

Для несущих деталей железнодорожного подвижного состава характерно то, что они испытывают действие статических нагрузок высокого уровня, обусловленных массой самих конструкций и массой груза, который воздействует на эти конструкции. Для локомотивов в статической нагрузке доминирует их собственная масса.

Суть его в том, что он учитывает динамическое воздействие на несущие узлы, обусловленных движением, в том числе по неровностям пути. Естественно, что неровности влияют и на динамические нагрузки, которые испытывают несущие узлы локомотивов. Причем очевидно, что динамические нагрузки, обусловленные движением по неровностям пути, имеют случайный характер, и, как следствие, в расчетной практике наблюдается тенденция к использованию вероятностных методов расчета [26, 27]. Можно с уверенностью сказать, что доминирующая составляющая динамических сил связана с проходом подвижным составом по стыкам. Для маневрового подвижного состава данный вид возмущающего воздействия является единственным из-за невысоких скоростей движения. При разработке расчетных оценок этому фактору следует уделить основное внимание.

На стыковых зазорах рельсового пути, как показывают многочисленные испытания

---

, узлы подвижного состава испытывают наибольшие ускорения. От этих ускорений в значительной мере зависит динамическая догрузка несущих узлов, представляющая основную причину накопления их повреждений.

В нормативной документации по расчету локомотивов приводятся эмпирические формулы по оценке коэффициентов динамики. Формулы получены в результате обработки экспериментальных данных и представляют возможность определить амплитудное значение динамических добавок при различных скоростях движения с учетом характеристик рессорного подвешивания.

Имея представление о частоте воздействия амплитудных значений динамических добавок, обусловленных стыковыми зазорами, которые проходит подвижной состав за срок службы, и имея уровень амплитуд динамических воздействий, можно сказать, что обеспечена необходимая база исходной информации для расчета коэффициента запаса сопротивления усталости и долговечности конструкции.

Коэффициенты динамики в нормативной документации отражают вероятностный характер динамических воздействий, а расчет числа циклов воздействий, исходя из прохода стыковых зазоров, имеет детерминированную структуру. Поэтому подход к построению расчетных зависимостей с использованием значений коэффициента динамики, полученных на основе Норм, можно будет определить, как детерминированную. Если же исходные данные по коэффициенту динамики определяются через решение соответствующей задачи динамики, такой подход можно назвать детерминированным.

Известно, что статические расчеты способствуют получению информации о наиболее нагруженных зонах несущих узлов подвижного состава. С позиции усталостных расчетов эти напряжения будут представлять средние напряжения цикла 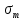. Если эти напряжения умножить на коэффициент динамики, то будут получены амплитуды переменных напряжений – 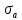. Частота нагружений, связанная с проходом стыков при тригонометрической аппроксимации неровностей, будет определятся как:
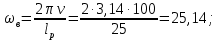(2.1)
где v – скорость движения, м/с; l_р – длина рельсового звена, м.

Зная пробег единиц подвижного состава, можно найти число стыковых воздействий за рассматриваемый период.

---

2.2 Построение простейших расчетных зависимостей по оценке напряженного состояния, влияющего на усталостные повреждения
Приведем общие формулы расчетов повреждающих напряжений. Максимальное напряжение 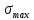будет определятся как:

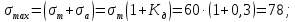(2.2)

где 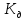– коэффициент динамики.

Минимальное напряжение цикла :

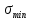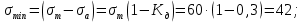(2.3)

Если принять, что все напряжения определяются через рассчитанные статические, то можно, реализуя расчет по оценке сопротивления усталости, решить задачу о допустимом уровне статических напряжений, при котором будет обеспечиваться необходимая усталостная прочность.

Воспользуемся известным соотношением, полученным на основе анализа диаграммы предельных напряжений Хейя [62]:

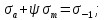(2.4)

где ψ – коэффициент чувствительности материала к асимметрии цикла, в частности он приведен в книге [62, с. 404]

Левую часть выражения (2.4) с учетом вышеприведенных значений можно переписать как: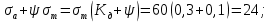

(2.5)

Если переписать значение предела усталостной прочности 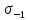с учетом факторов, влияющих на сопротивление деталей усталости, таких как размеры, качество обработки, технология повышения сопротивления усталости, концентрация напряжений, и обозначить их как 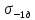, то коэффициент запаса по усталостной прочности – 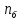, примет вид:

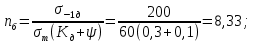(2.6)

Таким образом, получено выражение для оценки коэффициента запаса по схеме детерминировано-вероятностной оценки. Стоит отметить, что данное выражение идентично формуле

---

, указанной в Нормах.

Рассмотрим возможную схему оценки усталостной долговечности несущих деталей с использованием выбранной исходной информации. Для этого следует обратиться к уравнению наклонной линии кривой усталости [69]:

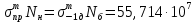(2.7)

где: 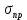– приведенная амплитуда циклического нагружения детали, равная

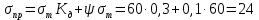(2.8)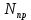

– число циклов нагрузки детали;

– предел выносливости прочности детали (см. выше);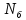

– базовое число циклов нагружения, ;

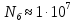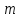– показатель степени, зависящий от угла наклона кривой усталости, который можно определить формулой, приведенной в книге [69]:

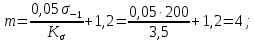(2.9)
– предел выносливости образца из материала детали;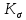

– эффективный коэффициент концентрации напряжений.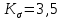

Общий вид кривой усталости представлен на рисунке 2.1


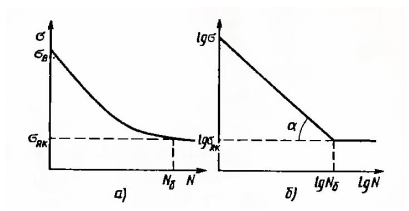
Рисунок 2.1 – Кривые усталости
На рисунке 2.1 представлены зависимости между максимальным напряжением 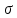и числом нагружений N, построенные в декартовых (рисунок 2.1, а) и логарифмических (рисунок 2.1, б) координатах.

Выше было получено выражение для амплитуды напряжений (2.5). С использованием (2.7) и (2.5) можно получить зависимость, которая определяет сопротивление усталости несущей детали подвижного состава с учетом числа циклов ее нагружения: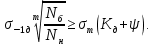

(2.10)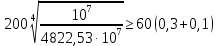



Долговечность несущей детали, измеряемую в количестве циклов, можно найти, воспользовавшись формулой (2.10), и она будет определяться зависимостью:

---

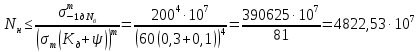(2.11)
Исходя из полученных результатов, можно написать выражение для оценки коэффициента запаса сопротивления усталости, используя формулу (2.10), в которой будет учитываться число циклов нагружения:
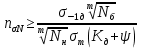(2.12)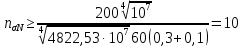



Следует иметь ввиду, что если амплитуда динамического воздействия не превосходит 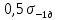, то такие амплитуды не учитываются в расчетах, поскольку, как принято считать, они не оказывают повреждающих воздействий [6].

В работах [73, 74] выражение (2.11) было применено для оценки выносливости и остаточного ресурса несущих конструкций тягового подвижного состава, а также рам тележек тепловозов ТЭМ2. Применение данного выражения показало удовлетворительные результаты сопоставимые со значениями, указанными в нормах и конструкторской документации.

Таким образом, сформированы основы для расчетной оценки коэффициента запаса сопротивления усталости и долговечности несущей детали. Расчет носит детерминированный подход и может быть использован для выполнения оценок.


2.4 Пример численной реализации расчетных формул
В книге [7] приводится пример прогнозирования надежности по условию обеспечения заданного значения коэффициента запаса усталостной прочности рамы тележки тепловоза ТЭМ2 в узле примыкания поперечной балки к боковине.

Результат расчета показал, что при сроке службы конструкции 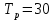лет обеспечивается допустимый уровень надежности. Данный расчет был выполнен на основе большого количества статистической информации, полученной в результате натурных испытаний конструкции.

В связи отсутствием экспериментальных данных о нагруженности рамы промышленных тепловозов в процессе эксплуатации, для проверки работоспособности подхода, описанного в предыдущем параграфе, выполним расчет несущего узла подвижного состава.

Используя исходные данные из книги [7], определим срок службы конструкции с использованием предложенного детерминированного подхода. Приняв, что: средние напряжения цикла

---

Смотрите также файлы

• .docx

• Анна. Андреевна Ахматова.docx

• Конспект зачётного мероприятия Галактика игр.docx

• Контрольная работа по дисциплине Финансовая среда предпринимательства и предпринимательские риски на отраслевых рынках.pdf

• Программа практическая психология.docx