ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 76
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
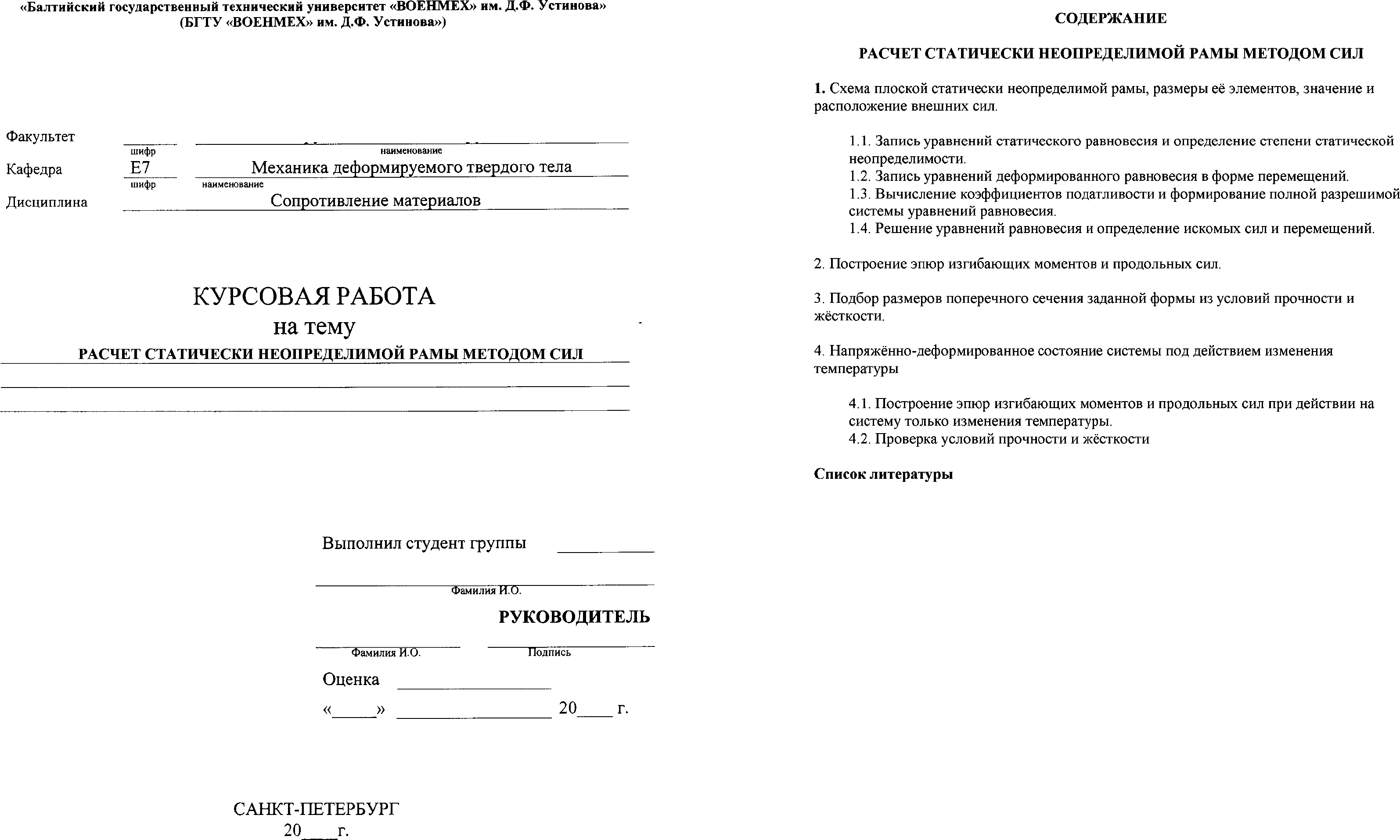
- Схема плоской статически неопределимой рамы, размеры её элементов, значение и расположение внешних сил
Система имеет два прямолинейных (длиной l) и один дугообразный (радиус l) участка, опирается на жёсткую заделку и неподвижный шарнир. Система нагружена сосредоточенной силой P и распределённой силой q, причём P = q*l. Поперечные сечения всех участков одинаковы и равны F, моменты инерции равны J, модуль продольной упругости материала равен E.
Поэтому УР имеют вид:
по оси X: X1 + X4 = 0
по оси Y: X2 + X5 + P - (q*2*l) = 0
по оси Z: X3 + X5*2*l – X4* l – P*l – (q*2*l) *l = 0
Система оказалась дважды внешне статически неопределима, поэтому потребуется получить два дополнительных уравнения для определения внешних неизвестных сил.
Для записи новых уравнений равновесия в форме уравнений равенства перемещений (УРП) пронумеруем все силы и соответствующие перемещения, Таким образом, возникают два вектора {P} и {Δ}, в которых на соответствующие места сразу можно поместить заданные или известные по условию задачи значения.
 X1
X1 X1
1
0
X
X
0
2
2
2
X3
X3
3 0
P X
X
, 0
4
4
4
X
X
0
5
5
5
P6
P
6 6
q q
Рис. 1.
7
7 7
Запись уравнений статического равновесия.
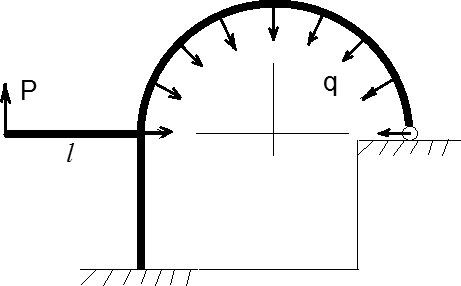
Равновесие данной системы требует записи трёх уравнений равновесия (УР) в направлении трёх осей координат, т.к. поступательное равновесие происходит вдоль глобальных осей X и Y, а вращательное равновесие вдоль перпендикулярной им оси Z. Расположение начала координат лучше выбрать так, чтобы силы (особенно неизвестные) имели минимальные плечи относительно оси Z. С этой точки зрения за начало координат выберем жёсткую заделку. Обозначим все внешние силы, действующие на конструкцию, как показано на рис. 2. и получим исходную систему (ИС).
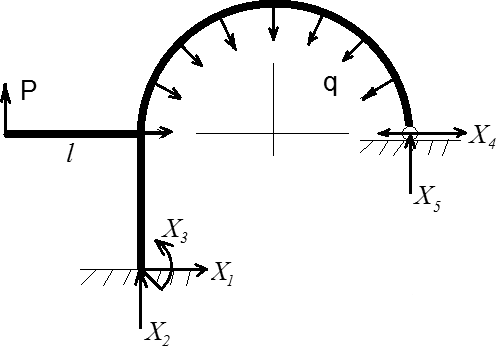
Рис. 2. Исходная система.
Запишем для этих векторов полную систему УРП:
δ11X1+ δ12X2+ δ13X3+ δ14X4+ δ15X5+ δ16P6+ δ17q7 = Δ1 δ21X1+ δ22X2+ δ23X3+ δ24X4+ δ25X5+ δ26P6+ δ27q7 = Δ2 δ31X1+ δ32X2+ δ33X3+ δ34X4+ δ35X5+ δ36P6+ δ37q7 = Δ3 δ41X1+ δ42X2+ δ43X3+ δ44X4+ δ45X5+ δ46P6+ δ47q7 = Δ4 δ51X1+ δ52X2+ δ53X3+ δ54X4+ δ55X5+ δ56P6+ δ57q7 = Δ5 δ61X1+ δ62X2+ δ63X3+ δ64X4+ δ65X5+ δ66P6+ δ67q7 = Δ6 δ71X1+ δ72X2+ δ73X3+ δ74X4+ δ75X5+ δ76P6+ δ77q7 = Δ7 ,
где δij – коэффициенты податливостей (КП), определяющие вклад каждой силы в общее перемещение.
ИС может быть преобразована так, чтобы данная система уравнений включала необходимые силы (коэффициенты при соответствующих силах не равны 0) и была статически определимой при вычислении податливостей. Кроме этого УР и УРП должны быть независимы с точки зрения определения значений неизвестных сил, поэтому в УРП количество неизвестных сил должно быть равно степени статической неопределимости (ССН). Поскольку такой выбор может быть сделан несколькими способами, то на первый план выступает схематическое удобство и простота вычислений, но, с другой стороны, появляется возможность проверки полученного решения с помощью любого другого набора сил.
Из общего числа УРП необходимо выбрать уравнения для тех перемещений, которые известны или заданы по условиям закреплений. В данном случае, как и в большинстве других, такими перемещениями являются нулевые. Сами уравнения для нулевых перемещений носят название канонических. Поэтому на основании ИС может быть создана эквивалентная система (ЭС) с теми же самыми нулевыми перемещениями, но сами направления перемещений приобретают податливость, т.е. связи на этих направлениях снимаются. Такой ЭС, например, может быть система, изображённая на рис. 3.
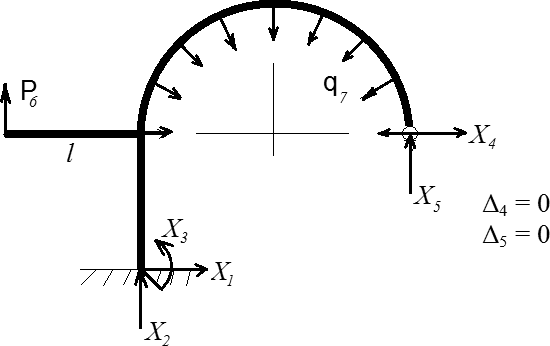 ij
ij NiNjdx
EF
MyiMyjdx EJ
Mzi Mz jdx EJ x
Mxi Mx jdx GJ y
Qyi Qyj dx GF z
Qzi Qz jdxGF
l l y l z l x l l
где ζx, ζy, ζz – коэффициенты, которые в большинстве случаев принимают значения близкие к 1, учитывающие форму поперечного сечения и распределение соответствующих напряжений по сечению;
N, Qy, Qz,, Mx, My, Mz – внутренние силы, возникающие в поперечных сечениях от приложенной соответствующей индексу единичной нагрузки.
Рис. 3. Эквивалентная система
Перемещения, для которых будут записаны канонические УРП, это Δ4 и Δ5. Данные уравнений можно решить относительно неизвестных сил, если определить коэффициенты
Вычисление интегралов делает необходимым разделение конструкции на однородные по геометрических характеристикам и свойствам материала стержневые элементы, в качестве которого можно принять даже участок дуги, если поперечный размер сечения составляет менее 1/5 от радиуса дуги. Таким образом, конструкция разделяется, как показано на схемах в таблице, на три участка. Поскольку наибольший вклад в КП дают интегралы от моментов, а в данном случае возникает только один изгибающий момент, который обозначен как Mz (внутренняя система координат в каждом
сечении ориентирована так, что направление глобальных и локальных осей z совпадают), то в данном вычисление КП будет проводится по упрощённой схеме как
податливостей. Для определения податливостей δij на основе ЭС определяется
вспомогательная система (ВС) (рис. 4), к которой следует приложить только единичную силу с соответствующим номером (второй индекс j коэффициента), чтобы вычислить перемещение в соответствующем направлении (второй индекс i коэффициента). Данное
ij
MziMz
1
l EJz
j dx
-
MziMz
2
1
l EJz
j dx
-
MziMz
3
l EJz
j dx
3
2
определение сразу позволяет сделать вывод, что податливости имеющие индексы неподвижных направлений тождественно равны 0.
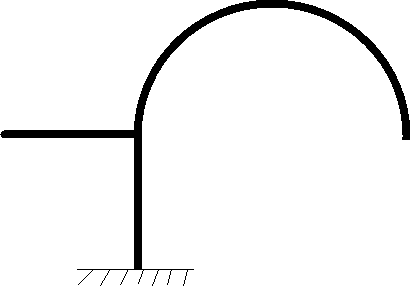
Рис. 4. Вспомогательная система
Таким образом, система канонических УРП приобретает вид: δ44X4+ δ45X5+ δ46P6+ δ47q7 = Δ4 = 0
δ54X4+ δ55X5+ δ56P6+ δ57q7 = Δ5 = 0
По числу КП видно, что единичные силы необходимо будет прикладывать в 4, 5, 6 и 7 направлениях, т.е. потребуются четыре вспомогательные системы: 4-я, 5-я, 6-я и 7-я ВС. Результаты работы с этими ВС удобно свести ив таблицу 1.
Процедура вычисления КП предполагает определение значений внутренних сил в поперечных сечениях и интегрирование по длине всех стержневых элементов конструкции в виде
т.е. в виде трёх интегралов для каждого участка.
-
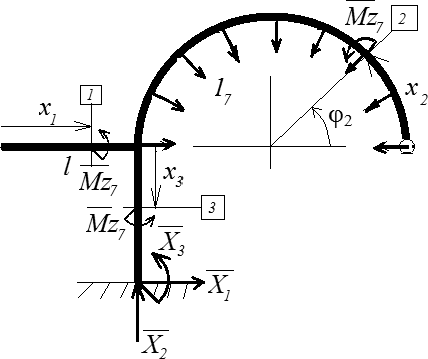
7ВС.
Уравнения равновесия X1 = 0
X2 - (17*2l) = 0
X3 – P*l – (17*2l) *l = 0
По x1: Mz7 = 0
По x2: Mz7 – 17* l2*(1 - cos(x2/l)) = 0 По x3: Mz7 – (17* 2l)*l = 0
Построение эпюр изгибающих моментов