ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 79
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
то остаётся только вычислить недостающие податливости и подставить найденные значения неизвестных сил. Если же искомого перемещения нет среди имеющихся (пронумерованных), то необходимо дать новому перемещению (и соответствующей силе) следующий номер по порядку и записать новое уравнение УРП. Поскольку все действующие силы уже должны иметь номера, то речь идёт о формальном введении новой силы, значение которой по условию эквивалентности должно быть равно нулю. На рис 5. изображена ЭС, в которой необходимо определить угол поворота в месте соединения всех участков. Для этого приложен нулевой момент 08. Автоматически это позволяет записать уравнение для 8-го перемещения.
| Интервал значений аргумента | Mz4 | Mz5 | Mz6 | Mz7 | Mz8 |
| 0 ≤ x1 ≤ l | 0 | 0 | x1 | 0 | 0 |
| 0 ≤ x2 ≤ πl | -l*sin(x2/l) | - l(1-cos(x2/l)) | 0 | - l2(1-cos(x2/l)) | 0 |
| 0 ≤ x3 ≤ l | x3 | -2l | l | 2l2 | -1 |
Вычисляются 4 новых интеграла податливостей:
Таблица 3.
1 2 3 4 5
l Mz Mz
lMzMz
l Mz Mz
δ84X4+ δ85X5+ δ86P6+ δ87q7 = Δ8
84 8 5 dx1 8 5 dx2 8 5 dx3
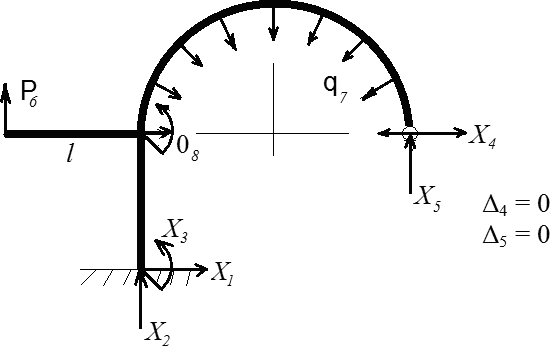 0 EJz
0 EJz0 EJz
0 EJz
l Mz Mz
lMzMz
l Mz Mz
85 8 5 dx1 8 5 dx2 8 5 dx3
0 EJz
0 EJz
0 EJz
l Mz Mz
lMzMz
l Mz Mz
86 8 5 dx1 8 5 dx2 8 5 dx3
0 EJz
0 EJz
0 EJz
l Mz Mz
lMzMz
l Mz Mz
87 8 5 dx1 8 5 dx2 8 5 dx3
0 EJz
0 EJz
0 EJz
Рис. 5. Эквивалентная система
Для вычисления податливостей потребуется 8-я ВС, изображенная на рис. 6, нагруженная соответствующей единичной силой.
В результате для 8-го перемещения имеем Δ8 = δ84X4+ δ85X5+ δ86P6+ δ87q7 =
- Подбор размеров поперечного сечения заданной формы из условий прочности и жёсткости.

Производится построение эпюр внутренних силовых факторов (продольной силы N b поперечного изгибающего момента Mz).
Определяется самое опасное сечение.
В самом опасном сечении записывается условие прочности по самой опасной точке и определяется безопасный размер сечения заданной формы
Круглое сечение
2 2
В самой опасной точке σэкв= √σ+ 4τ ≤ [ σ]
d =
Подстановка полученного значения размера в условие прочности по самой опасной точке и проверка того, что максимальная величина эквивалентного напряжения составляет 95% - 98% предела прочности.
Квадратное сечение
-
Напряжённо-деформированное состояние системы под действием изменения температуры
Тепловой расчёт выполняется при условии нагрева системы на величину ΔT без внешнего силового воздействия, как показано рис. 7. Коэффициент линейного теплового расширения α выбирается как у стали и равен 10-5
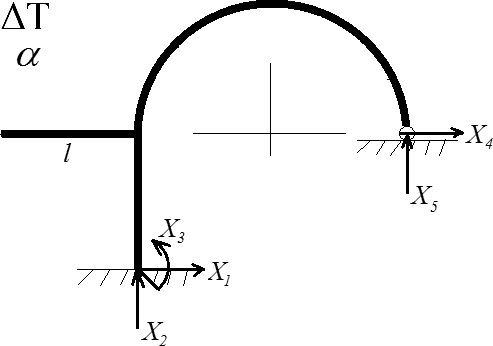
Рис. 7. Исходная система.
В этом случае УР имеют вид: по оси X: X1 + X4 = 0
по оси Y: X2 + X5 = 0
по оси Z: X3 + X5*2*l – X4* l = 0
Эквивалентная система остаётся прежней. Система канонических УРП приобретает вид:
δ44X4+ δ45X5+ δ4T ΔT = Δ4 = 0 δ54X4+ δ55X5+ δ5T ΔT = Δ5 = 0
Коэффициент температурной податливости
В самой опасной точке σ
экв
= √σ2+ 4τ2≤ [ σ]
Ndx
Ndx
N dx
iT i 1
a = l1
i 2
l2
i 3
l3
Подстановка полученного значения размера в условие прочности по самой опасной точке и проверка того, что максимальная величина эквивалентного напряжения составляет 95% - 98% предела прочности.
По формуле перемещения указанной точки С записывается условие жёсткости ΔС = δС4X4+ δС5X5+ δС6P6+ δС7q7 ≦ [Δ]
Размер поперечного сечения корректируется таким образом, чтобы перемещение
было меньше заданного предела (95-98%)
Коэффициенты податливости от сил остаются прежними как в предыдущем расчёте.
Вспомогательные системы используются для построения эпюр вспомогательных продольных сил
Таблица 4.
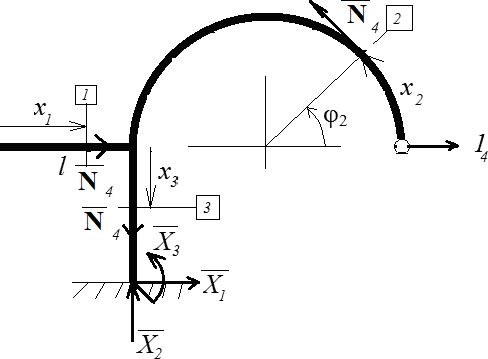 | 4ВС. Уравнения равновесия X1 + 14 = 0 X2 = 0 X3 – 14* l = 0 По x1: N4 = 0 По x2: N4 - 14*sin(x2/l) = 0 По x3: N4 = 0 |
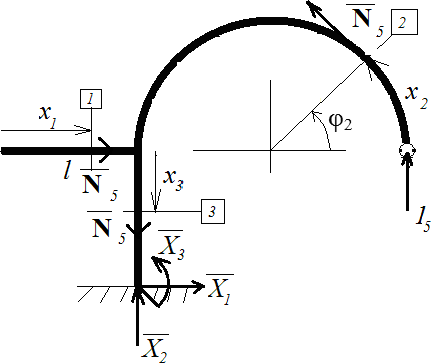 | 5ВС. Уравнения равновесия X1 = 0 X2 + 15 = 0 X3 + 15*2l = 0 По x1: N5 = 0 По x2: N5 + 15* cos(x2/l) = 0 По x3: N5 - 15 = 0 |
Таблица 5.
| Интервал значений аргумента | N4 | N5 |
| 0 ≤ x1 ≤ l | 0 | 0 |
| 0 ≤ x2 ≤ πl | sin(x2/l) | -cos(x2/l) |
| 0 ≤ x3 ≤ l | 0 | 1 |
В результате решения уравнений определяются реакции опор от теплового воздействия и сравниваются с аналогичными от силового воздействия. Делается вывод о влиянии колебаний температур на прочность