Файл: Имеет.docx

Скачать файл (0,20Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 24.11.2023

Просмотров: 81

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

j dx

l Mz Mz

На каждом участке обозначено поперечное сечение с соответствующим номером, направлением движения x и внутренний изгибающий момент Mz, на оси которого будут записываться уравнения равновесия для выделенной (отсечённой) координатой x части участка. В правой колонке таблицы 1. выписаны уравнения равновесия и соответствующие выражения для Mz.

Таблица 1.
В данном случае при определении значений Mz участки были выбраны так, что отпала необходимость в определении значений реакций опоры. Полученные выражения Mz переносятся в таблицу 2.

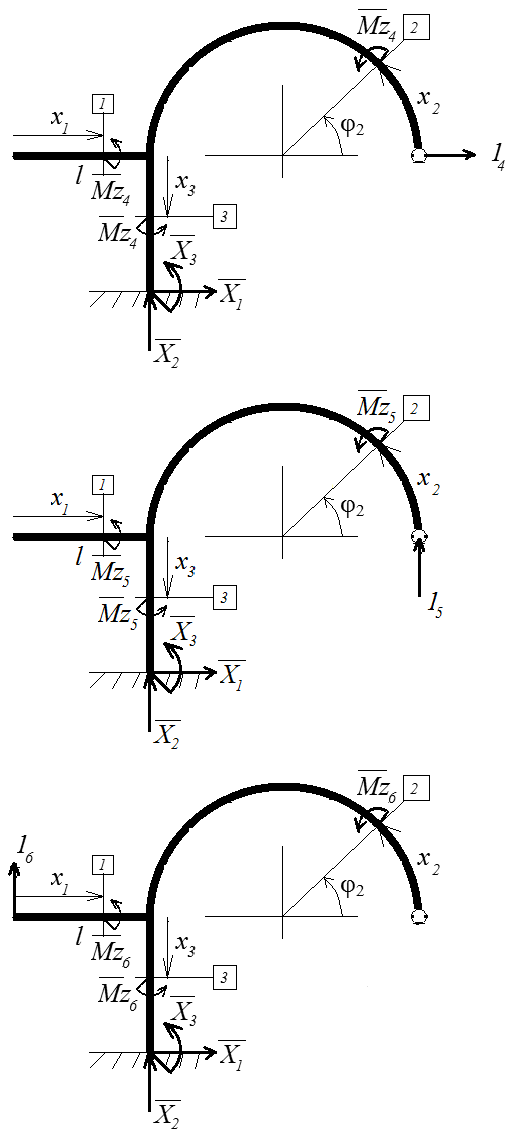
	4ВС. Уравнения равновесия ^X1 ⁺¹4 ⁼⁰ ^X2 ^{= 0} ^X3 ^–¹4^{* l}^{= 0} ^{По x}1^:^Mz4 ^{= 0} ^{По x}2^{: Mz}4 ^{+ 1}4^{* lsin(x}2^{/l) = 0}^{По x}3^:^Mz4 ^–¹4^^x3 ^{= 0}
	5ВС. Уравнения равновесия ^X1 ⁼⁰ ^X2 ^{+ 1}5 ^{= 0}^X3 ⁺¹5^2l⁼⁰ ^По^x1^:^Mz5 ^{= 0} ^{По x}2^{: Mz}5 ^{+ 1}5^{ l(1 - cos(x}2^{/l)) = 0}^{По x}3^:^Mz5 ^{+ 1}5^^2l^{= 0}
	6ВС. Уравнения равновесия ^X1 ⁼⁰ ^X2 ^{+ 1}6 ^{= 0}^X3 ^–¹6^l⁼⁰ ^{По x}1^:^Mz6 ^–¹6^^x1 ^{= 0}^{По x}2^:^Mz6 ⁼⁰ ^По^x3^:^Mz6 ^–¹6^*^{l =}⁰

Таблица 2.

Интервал значений аргумента	^Mz4	^Mz5	^Mz6	^Mz7
^{0 ≤}^x1 ^≤^l	0	0	^x1	0
^{0 ≤}^x2 ^≤^πl	^-^l^*sin(x2^/l)	^-^l^(1-cos(x2^/l))	0	^-^l2^(1-cos(x2^/^l⁾⁾
^{0 ≤}^x3 ^≤^l	^x3	-2l	l	2l²

Запишем выражения для всех необходимых КП:

_^lMzMz

^^lMzMz

1 2 3 4 5

^l Mz Mz

44 ^_

0

EJ_z

dx₁ _

0

EJ_z

dx₂ _

0

EJ_z

dx₃

^l Mz Mz

^^lMzMz

^l Mz Mz

 ₄₅ _^{4 5}dx₁ _^{4 5}dx₂ _^{4 5}dx₃₅₄

₀EJ_z

₀EJ_z

₀EJ_z

^l Mz Mz

^^lMzMz

^l Mz Mz

 ₄₆ _^{4 6}dx₁ _^{4 6}dx₂ _^{4 6}dx₃

₀EJ_z

₀EJ_z

₀EJ_z

^l Mz Mz

^^lMzMz

^l Mz Mz

 ₄₇ _^{4 7}dx₁ _^{4 7}dx₂ _^{4 7}dx₃

₀EJ_z

₀EJ_z

₀EJ_z

^l Mz Mz

^^lMzMz

^l Mz Mz

₅₅ _^{5 5}dx₁ _^{5 5}dx₂ _^{5 5}dx₃

₀EJ_z

₀EJ_z

₀EJ_z

^l Mz Mz

^^lMzMz

1 2 3 4 5

^l Mz Mz

₅₆ _^{5 6}dx₁ _^{5 6}dx₂ _^{5 6}dx₃

₀EJ_z

₀EJ_z

₀EJ_z

^l Mz Mz

^^lMzMz

^l Mz Mz

₅₇ _^{5 7}dx₁ _^{5 7}dx₂ _^{5 7}dx₃

₀EJ_z

₀EJ_z

₀EJ_z

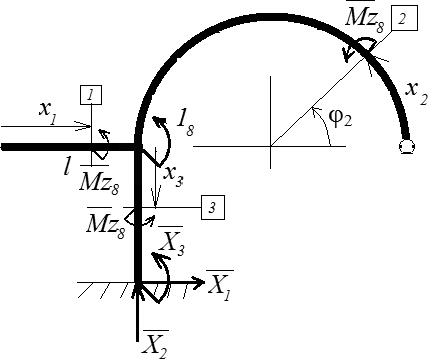8ВС.
Уравнения равновесия ^X1 ⁼⁰

^X2 ⁼⁰

^X3 ^{+ 1}8 ⁼⁰
^{По x}1^{: Mz}8 ^{= 0}^По^x2^:^Mz8 ⁼⁰

^По^x3^:^Mz8 ⁺¹8⁼⁰

Система уравнений приобретает вид ^δ44^X4^{+ δ}45^X5⁺^δ46^P6⁺^δ47^q7 ⁼⁰

^δ54^X4⁺^δ55^X5⁺^δ56^P6⁺^δ57^q7 ⁼⁰

^X1 ⁼^X2⁼^X3 ⁼^X4 ⁼^X5 ⁼

Решение системы УРП и УР даёт:

Определение перемещений в статически неопределимой системе представляет не менее важную задачу, поэтому этот аспект рассмотрим подробнее. Если искомое перемещение уже есть в списке перемещений вектора {Δ} и входит в систему УРП, например
^δ64^X4⁺^δ65^X5⁺^δ66^P6⁺^δ67^q7 ⁼^Δ6
Рис. 6. 8-я вспомогательная система
В таблице 3 заполняется незаполненная в таблице 2 колонка, которая и была предусмотрена под новую ВС.