Файл: Контрольная работа по дисциплине Математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЧАСТНОЕ ОРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ ТЕХНОГОЛОГИЙ УПРАВЛЕНИЯ
И ЭКОНОМИКИ»
Институт Международных программ
Кафедра Международных финансов и бухгалтерского учета
Контрольная работа
по дисциплине «Математический анализ»
Бахриев Шахриёр
Выполнила студентка: 1 курс, ВэМПб-Э06-21-1
Руководители: Пушкина В.П.
Санкт-Петербург
2022 г.
Тема № 3. Предел и производная функции одной переменной
3.1. С помощью методов дифференциального исчисления исследовать и построить график функции
у =
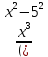 допустим у = 0
допустим у = 0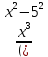 = 0
= 0 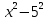 = 0 найдём значения х, при которых знаменатель дроби = 0
= 0 найдём значения х, при которых знаменатель дроби = 0х = 5; -5
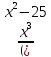 = 0 х
= 0 х 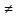 5; -5
5; -5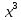 = 0
= 0х = 0
у =
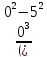 допустим х=0
допустим х=0у = 0
точки перегиба (0;0)
Тема № 4. Интегральное исчисление функции одной переменной
4.1.Найти интеграл
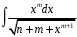 .
.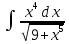
dх =
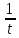 dх , где t=
dх , где t= 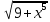 и t'=
и t'= 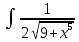 * 5*4
* 5*4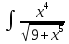
*
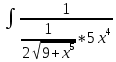 * dх сокращаем
* dх сокращаем 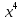
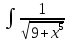 *
* 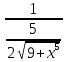 * dt упростим дробь
* dt упростим дробь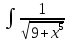 *
* 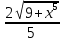 *dt сокращаем
*dt сокращаем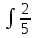 dt
dt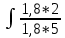 dх по формуле
dх по формуле 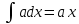
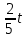
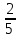 *
*  + C, C
+ C, C 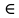 R
R4.2.Найти интеграл
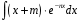 .
.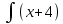 *
* 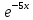 dx u= х +4 dv=
dx u= х +4 dv= 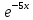 dx
dxdu =(х` + (4)`) dx
du =(1 + 0) dx
du =dx
v =-
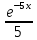 подставляем
подставляем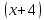 * -
* - 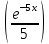
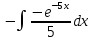
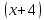 * -
* - 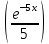 +
+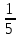 *
* 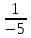 *
* 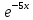
Ответ: -
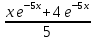 -
- 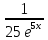 + C, C
+ C, C 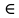 R
R4.3. Найти интеграл
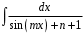 .
.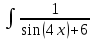 dх подставляем t=4х
dх подставляем t=4х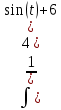
dt
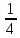 ×
×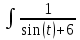 dt
dt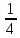 ×
×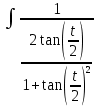 +6 подставим дифференциал
+6 подставим дифференциалdt=
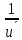 ×du, где u=
×du, где u=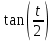 и
и u΄=
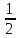 ×
×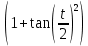
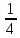 ×
×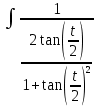 ×
×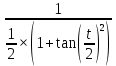 du
du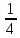 ×
×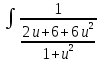 ×
×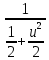 du
du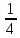 ×
×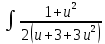 ×
×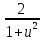 du
du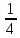 ×
×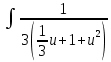 du
du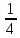 ×
×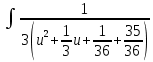 du
du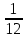 ×
×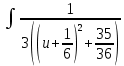 du используя
du используя 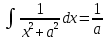
найдем интеграл
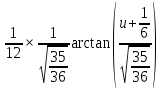
Сделаем обратную замену u=tan
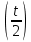
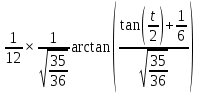
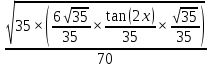
Прибавим константу интегрирования С
 R
RОтвет:
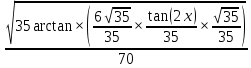 +C, С
+C, С
R
4.4. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
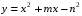 ,
, 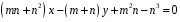 .
.у =
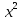 + 4х -25 , - парабола, с ветвями вверх 45х – 9у – 45 = 0 */:9
+ 4х -25 , - парабола, с ветвями вверх 45х – 9у – 45 = 0 */:95х – у – 5 = 0
Построим заданные линии
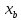 =
= 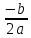 =
= 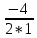 = -2 ;
= -2 ; 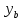 = y(
= y(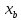 ) = 4-8-25 =-29
) = 4-8-25 =-29(-2; -29) – координаты вершины параболы
у=0
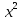 + 4х – 25 = 0
+ 4х – 25 = 0 D= 16 – 4*1*(-25) = 116
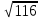 = 2*
= 2* 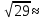 10,8
10,8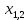 =
= 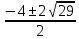
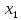 = -2 +
= -2 + 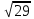
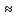 3,4
3,4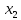 = -2 -
= -2 -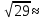 -7,4
-7,45х -у – 5 = 0 - прямая линия х -2 2
у = 5х – 5 у -15 5
Найдём точки пересечения линий:
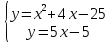
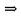
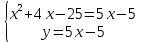
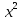 – х -20 = 0
– х -20 = 0D= 1-4*1*(-20) = 81;
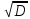 =9
=9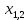 =
= 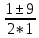
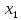 =
= 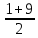 = 5
= 5 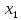 =
= 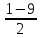
= -4
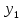 = 5*5-5=20
= 5*5-5=20 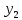 = 5*(-4)-5=-25
= 5*(-4)-5=-25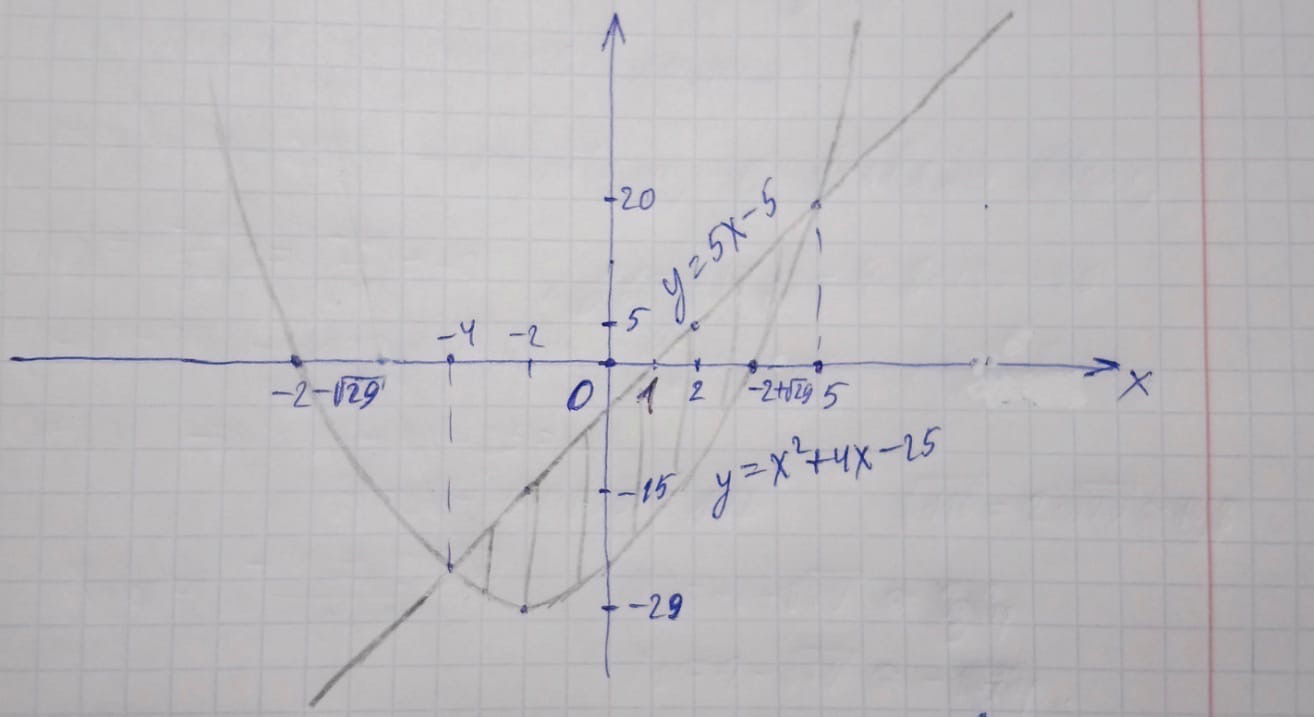
Вычислим S заштрихованной фигуры
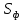 =
= 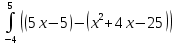
dx=
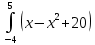
dx= (
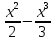 + 20х)
+ 20х)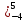 = = (
= = (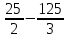 + 100)- (
+ 100)- (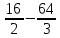 + 80)= 180 +
+ 80)= 180 +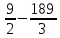 = 180 + 4,5 – 63 = 121,5
= 180 + 4,5 – 63 = 121,5Ответ:
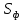 = 121,5
= 121,5 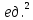
Тема № 5. Дифференциальное исчисление функции нескольких переменных.
5.1. Найти дифференциал
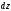 функции
функции 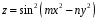 .
.sin (4
 - 5
- 5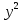 )
)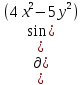 найдем производную по х
найдем производную по хcos
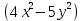 * 10х
* 10хcos
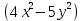 * (-10у) найдём производную по у
* (-10у) найдём производную по у10cos
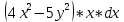 - 10cos
- 10cos