Файл: Моделирование, кинематическое и динамическое исследование и симуляция манипулятора с 5 степенями свободы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 66
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(2)
Положение рабочего органа, то есть положение и ориентация по отношению к системе отсчета основания, могут быть получены из их конкатенации следующим образом:
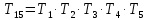 (3)
(3)Где с последней матрицей мы анализируем ориентацию рабочего органа.
Фактически путем подстановки параметров Денавита-Хартенберга получается следующая однородная матрица трансформации:
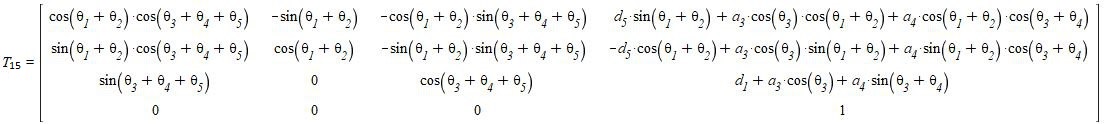
(4)
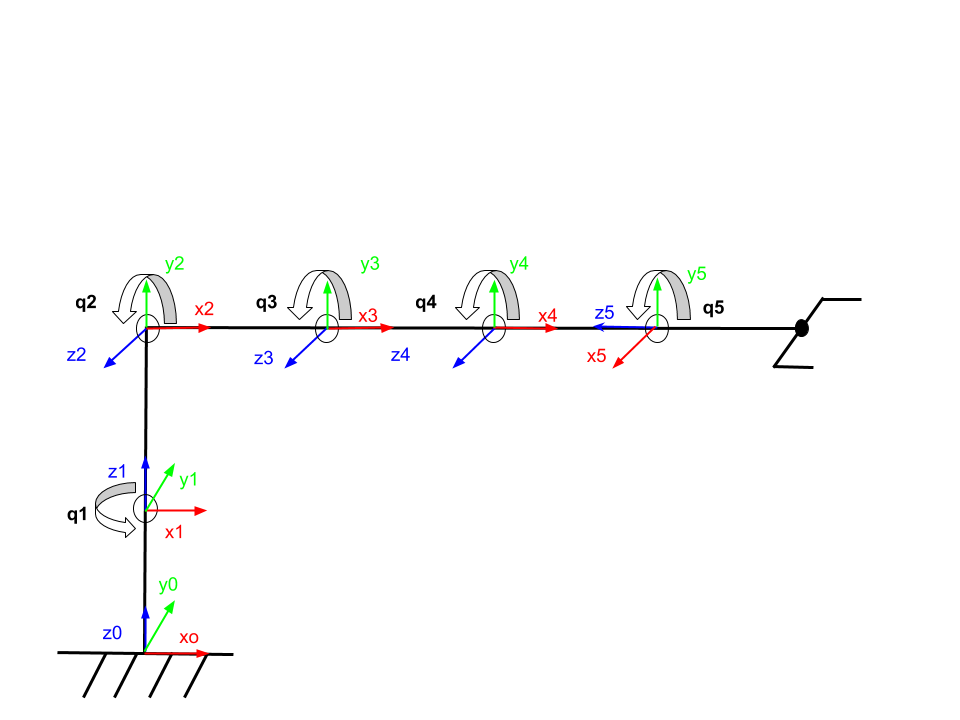 Таким образом, системы отсчета, применяемые к каждому суставу, определяются следующим образом:
Таким образом, системы отсчета, применяемые к каждому суставу, определяются следующим образом:Рис. 3. Системы отсчета, связанные с суставами.
2. Кинематический анализ
К изучению кинематики, т. е. к описанию движения серийного манипулятора, можно подойти, рассмотрев две дополняющие друг друга задачи, а именно прямую и обратную кинематику.
Р
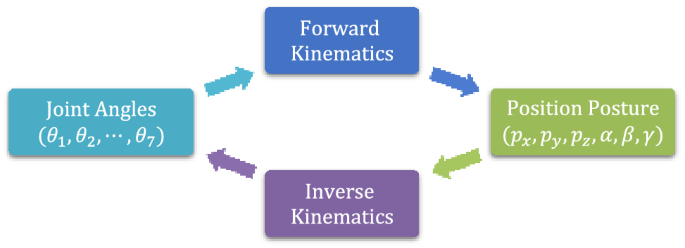
ис. 4. Блок-схема процесса кинематического анализа.
2.1 Планирование траектории
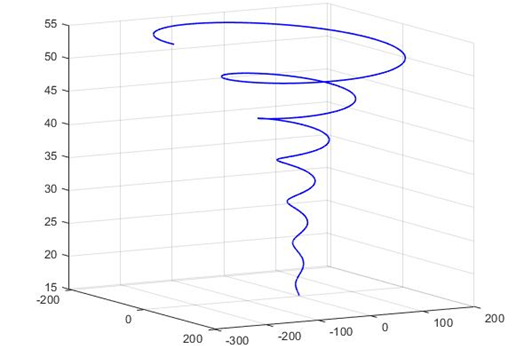
Предполагаемая траектория рабочего органа представляет собой логарифмическую спираль, выраженную в параметрической форме, т.е.:
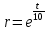
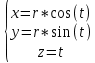
(
5)
Рис. 5. Логарифмическая спираль в пространстве
Следует отметить, что затем значение t будет заменено на этапе моделирования временем дискретизации.
2.2 Прямая кинематика
Чтобы получить матрицу, описывающую прямую кинематику, необходимо сцепить матрицы преобразования каждого шарнира:
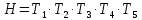 (6)
(6)Тогда получим следующую матрицу:

(7)
Где отдельные элементы соответственно:
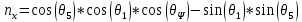
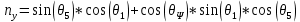
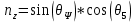 (8)
(8)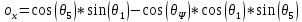
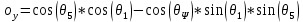
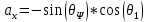 (9)
(9)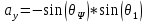
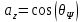 (10)
(10)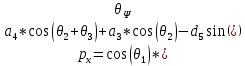
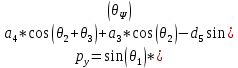
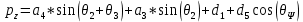 (11)
(11)Символ ѱ указывает на “Wrist Angle Relative to Ground”, постоянный угол, который представляет поворот запястья робота по отношению к остальной части руки.
Поскольку начальная поза робота была выбрана как та, которую он принимает в своей нулевой конфигурации, θi = {0} используется в качестве начальных значений углов совместных переменных, получая следующую числовую матрицу:
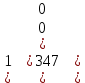
H =
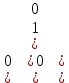
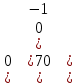
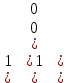
(12)
2.3 Обратная кинематика
При решении обратной задачи кинематики используется алгебраический подход. С помощью уравнений px, py, pz, рассчитанных в прямой кинематике, определяются формулы для расчета величины угла каждого шарнира.
Для получения значения угла θ1 рассматриваются соответствующие числовые значения выражений px, py, называемые x и y, и записывается следующее тригонометрическое соотношение:
Для определения шарнирного угла θ2, связанного со вторым звеном, необходимо учитывать равенства:
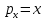 (14)
(14) 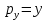 (15)
(15) И
(16)
Относительно следующего равенства:
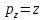 (17)
(17)Предполагая, что z указывает числовое значение, связанное с pz, мы имеем это:
(18)
г
(19)
Этот угол Вартга по конструкции задается равным 0° таким образом, чтобы предположить, что невозможно изменить ориентацию захвата, которым робот захватывает возможный объект, подлежащий захвату.
В
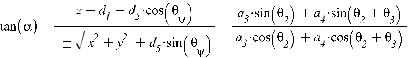 ыполняя связь член-к-члену между [18] и [16], мы получаем, что:
ыполняя связь член-к-члену между [18] и [16], мы получаем, что:(20)
Проводя различные алгебраические переходы и перерабатывая это выражение с помощью тригонометрических формул, получаем:
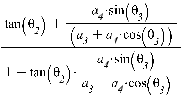
(21)
Последнее можно проследить до суммы тангенса, на самом деле:
(22)
(23)
Отсюда можно вывести, что:
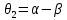 (24)
(24)Чтобы вычислить совместную переменную θ3, найдите значение
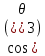 из суммы квадратов между [16] и [18], получив:
из суммы квадратов между [16] и [18], получив: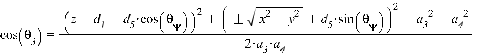
(25)
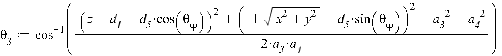 Из которого θ3 можно определить по следующей зависимости:
Из которого θ3 можно определить по следующей зависимости:(26)
Наконец, что касается θ5, используются следующие уравнения, полученные из прямой кинематики:
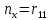 (28)
(28)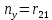 (29)
(29)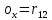 (30)
(30)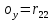 (31)
(31)где rij обозначает соответствующее числовое значение.
В этот момент для определения значения
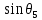 достаточно написать:
достаточно написать: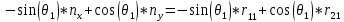
(32)
Из чего получаем:
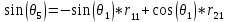 (33)
(33)Аналогично, для значения
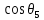 будем иметь:
будем иметь: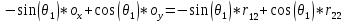 (34)
(34)Из чего получаем:
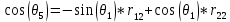 (35)
(35)Наконец, θ5 рассчитывается по формуле арктангенса:
(36)
3. Модель Simscape MultiBody
Для того, чтобы иметь возможность имитировать установленное для робота движение, использовалась программная среда Simulink, в частности, ссылаясь на библиотеку Simscape.
Используя пакеты, доступные в подбиблиотеке Multibody, удалось создать следующую модель:
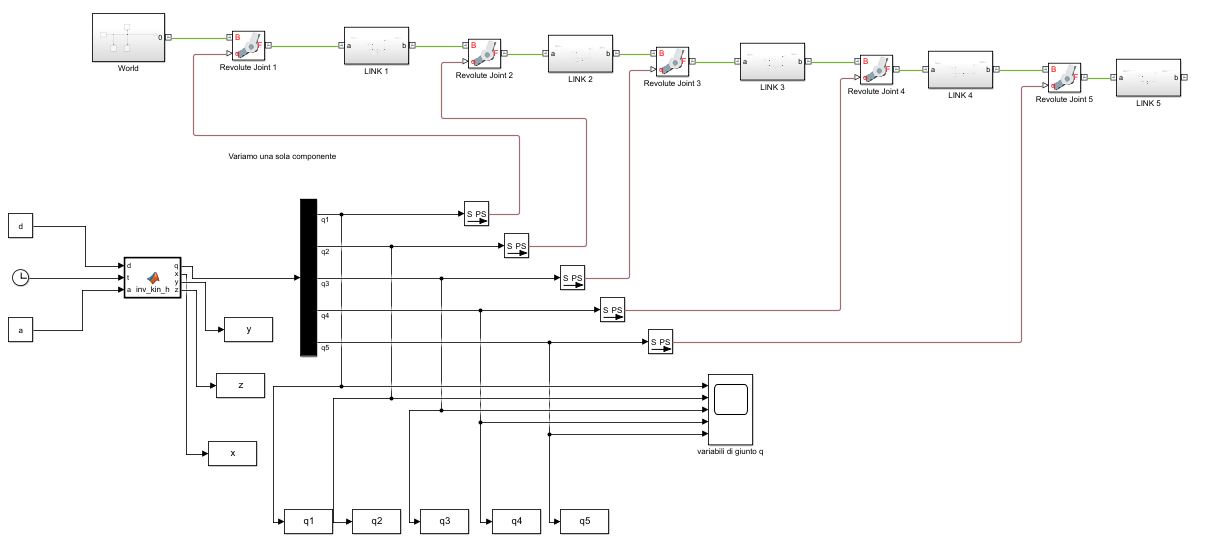
Рис. 6. Модель Simulink робота 5DOF
В частности, в блоке MatlabFunction "inv_kin_h" уже описанный ранее алгоритм кинематической инверсии реализован путем задания заданной траектории рабочего органа. Блок получает на вход векторы, содержащие параметры Денавита-Хартенберга и время дискретизации, используемое при моделировании, через часы. На выходе он вернет значение углов, связанных с переменными соединения, и положением, выраженным в декартовых координатах (x, y, z), принимаемых инструментом момент за моментом.
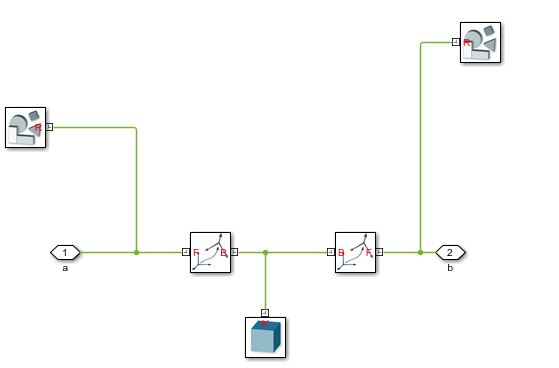 «Физическая» реализация робота происходит в верхней части модели Simulink, где были созданы различные звенья, соединенные друг с другом Revolute Joints. Пример показан на рисунке ниже:
«Физическая» реализация робота происходит в верхней части модели Simulink, где были созданы различные звенья, соединенные друг с другом Revolute Joints. Пример показан на рисунке ниже:Рис. 7. Пример ссылки, смоделированной в Simulink
Каждое звено представлено «телом», определяющим его физическую форму, парой систем отсчета и двумя «жесткими преобразованиями», посредством которых задаются перемещения и повороты звена.
Каждое Revolute Joint настроено на получение изменений, испытываемых каждым углом, чтобы гарантировать желаемое движение.
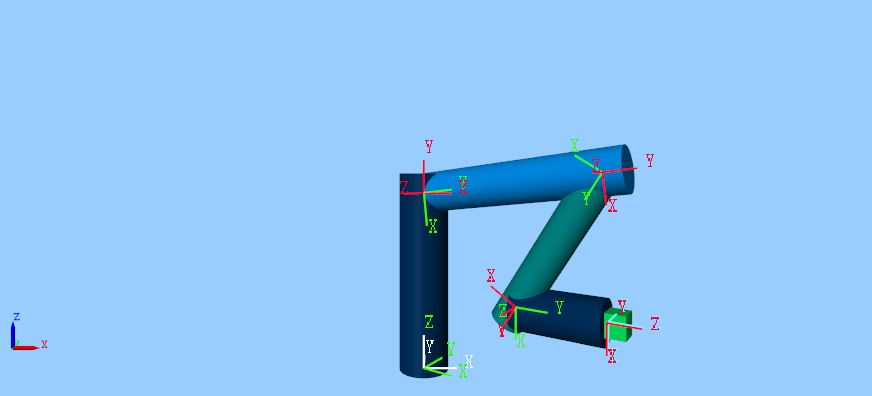
Рис. 8. Модель робота с 5 степенями свободы
4. Анализы и результаты
В этом разделе мы рассмотрим часть проверки алгоритма кинематической инверсии, реализованную с использованием алгебраического метода.
Принятая стратегия состоит в том, чтобы использовать значения, определенные для совместных переменных, в части, относящейся к инверсной кинематике, чтобы затем заменить их в матрице, которая описывает прямую кинематику рассматриваемого робота.
4.1 Выделение данных
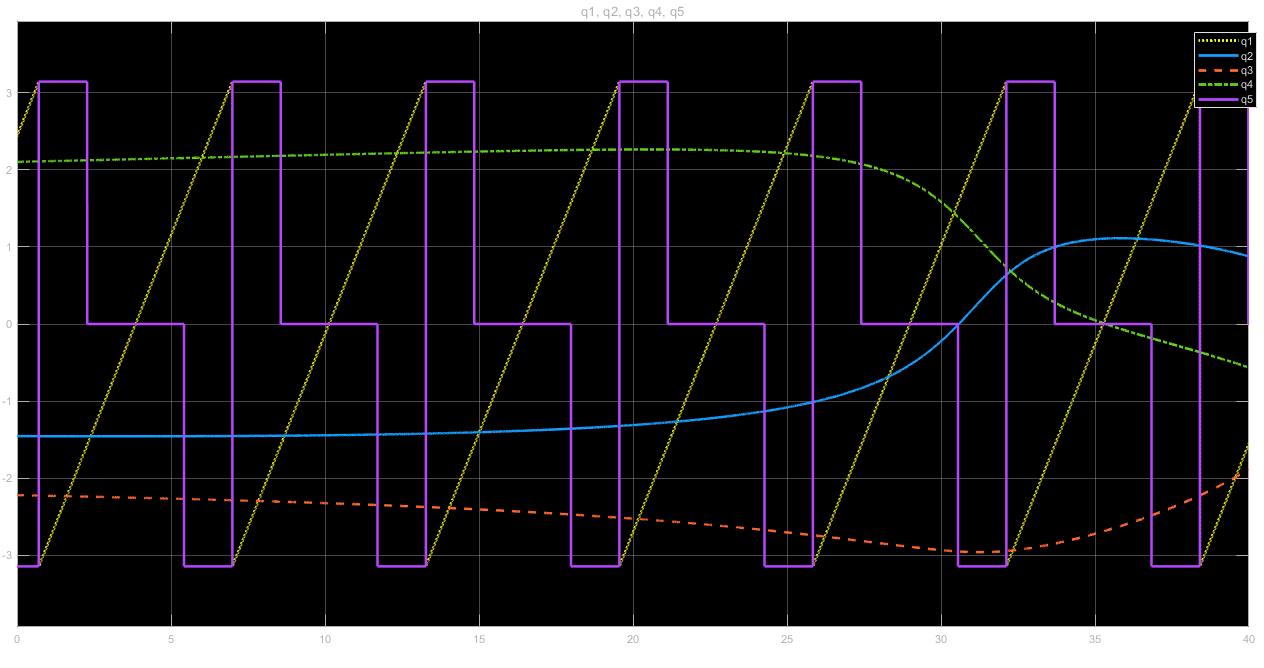 Данные, полученные после моделирования, были экспортированы в рабочее пространство Matlab с использованием соответствующих блоков Simulink, как показано на ранее представленной блок-схеме. Полученные значения совместных переменных были собраны в векторы, из которых были извлечены выборки для использования для проверки.
Данные, полученные после моделирования, были экспортированы в рабочее пространство Matlab с использованием соответствующих блоков Simulink, как показано на ранее представленной блок-схеме. Полученные значения совместных переменных были собраны в векторы, из которых были извлечены выборки для использования для проверки.Рис. 9. Совместные значения, полученные из обратной кинематики.
4.2 Проверка и результаты
Процедура проверки, чтобы продемонстрировать, что траектория, выполняемая конечным рабочим органом, точно соответствует той, которая была выбрана в первом случае, была реализована с помощью сценария Matlab, где, выбрав шаг выборки 1000, чтобы получить 16 значений по время, каждый сустав плюс конечное значение каждого из них позволяет приступить к расчету позы, принятой конечным рабочим органом, решая непосредственную кинематику рассматриваемого робота. На самом деле, для каждого набора значений совместных переменных, извлеченных в конкретный момент времени t, будет вычислено их положение в декартовых координатах. После этого было проверено, что найденные точки действительно принадлежат искомой траектории, что видно из рисунка ниже.
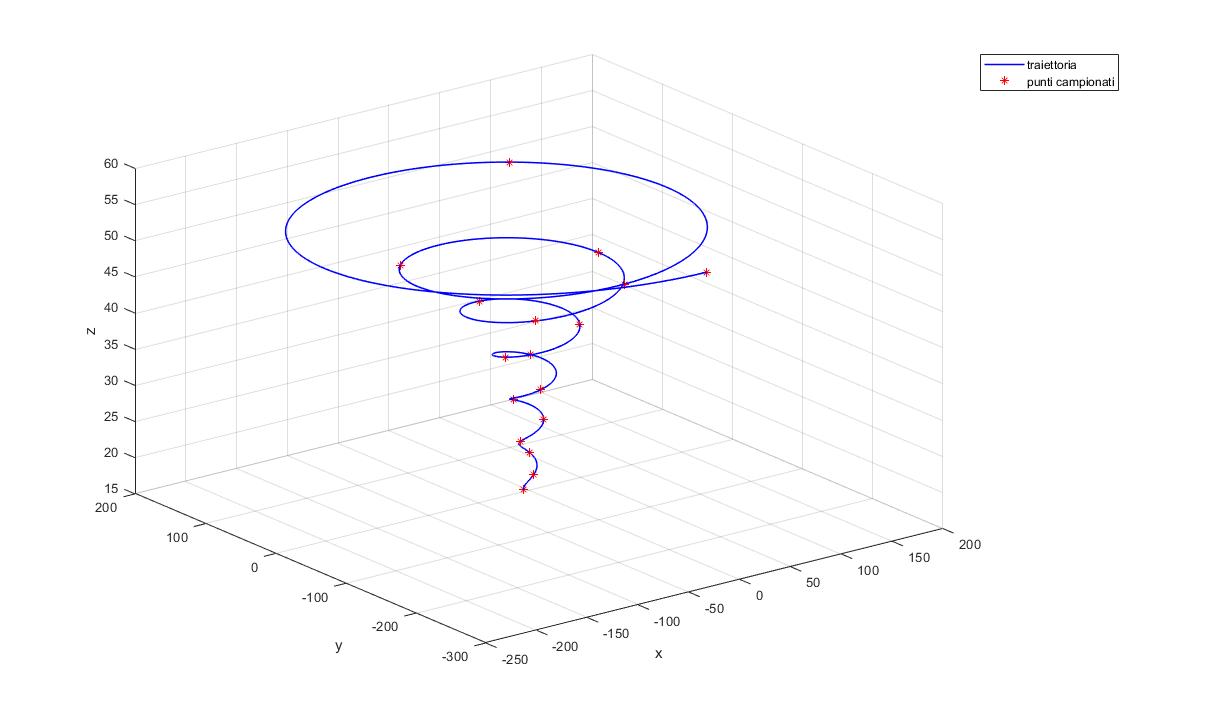
Рис. 10. Точки, определяемые обратной кинематикой, принадлежащие траектории.
5. Динамический анализ
Предметом динамики манипулятора как раздела робототехники является математическое описание действующих на манипуляторе сил и моментов в форме уравнений динамики движения. Также уравнения необходимы для моделирования движения манипулятора с помощью ЭВМ, при выборе законов уравнения и при оценке качества кинематической схемы и конструкции манипулятора.
Задача управления включает задачу формирования динамической модели реального манипулятора и задачу выбора законов или стратегий управления, обеспечивающих выполнение поставленных целей.
Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновой или лагранжевой механики. Результатом применения этих законов является уравнения, связывающие действующие в сочленениях силы и моменты с кинематическими характеристиками и параметрами движения звеньев.