Таким образом, уравнения динамики движения реального манипулятора могут быть получены методами Лагранжа-Эйлера или Ньютона-Эйлера. Уравнения Лагранжа-Эйлера обеспечивают строгое описание динамики манипулятора. Их можно использовать для решения прямой и обратной задачи динамики.

Прямая задача состоит в том, чтобы по заданным силам и моментам определить обобщённые ускорения, интегрирование которых позволит получить значения обобщённых координат и скоростей.

Обратная задача динамики заключается в том, чтобы по заданным обобщённым координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты.

Для решения обеих задач, как правило, необходимо вычислить динамические коэффициенты 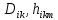и 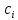. Вычисление этих коэффициентов требует выполнения очень большого числа арифметических операций. В связи с этим уравнения Лагранжа-Эйлера без дополнительных упрощений практически неприменимы для управления манипулятором в реальном времени.
5.1 Метод Лагранжа-Эйлера

Полное описание движения манипулятора можно получить, применяя метод Лагранжа-Эйлера для неконсервативных систем. Описав кинематику манипулятора с помощью матричного представления Денавита-Хартенберга, можно получить уравнение динамики. Такое совместное использование Д-Х-представления и метода Лагранжа приводит к компактной векторно-математической форме уравнений движения, удобной для аналитического исследования и допускающей реализацию на ЭВМ.

Вывод уравнений динамики движения манипулятора основан на следующем:

1. На описании взаимного пространственного расположения систем координат i-го и (i-1)-го звеньев с помощью матрицы преобразования однородных координат 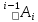. Эта матрица преобразует координаты произвольной точки относительно i-й системы координаты этой же точки относительно (i-1)-й системы координат.

2. На использовании уравнения Лагранжа-Эйлера:




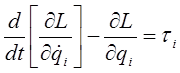
(37)

где L-функция Лагранжа

---

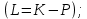
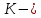
полная кинетическая энергии манипулятора;

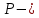полная потенциальна энергия манипулятора;

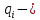обобщённые координаты манипулятора;

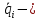первая производная по времени обобщённых координат;

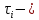обобщённые силы (или моменты), создаваемые в i-м сочленении для реализации заданного движения i-го звена.

Для того, чтобы воспользоваться уравнением Лагранжа-Эйлера, необходимо выбрать систему обобщённых координат. Обобщённые координаты представляют собой набор координат, обеспечивающий, полное описание положения рассматриваемой физической системы в абсолютной системе координат. Существуют различные системы обобщенных координат, пригодные для описания простого манипулятора с вращательными и поступательными сочленениями. Однако, поскольку углы поворотов в сочленениях непосредственно доступны измерению с помощью потенциометров или других датчиков, то они составляют наиболее естественную систему обобщенных координат. В этом случае обобщённые координаты совпадают с присоединенными переменными манипулятора. В частности, если i-е сочленение вращательное, то 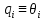, если же i-е сочленение поступательное, то .
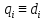5.2 Обратная динамика

Обратная задача динамики заключается в том, чтобы определить крутящий момент, необходимый для каждого из приводов робота, с учетом текущего положения и скорости, и желаемого ускорения. Эта информация важна на этапах моделирования проекта для определения требуемых характеристик привода, которые будут использоваться на физическом прототипе. Кроме того, расчет обратной динамики можно использовать в алгоритме управления крутящим моментом. Чтобы вычислить обратную динамику всей руки, мы сначала считаем связи робота между рукой и рабочим органом жесткими. Используя кинематику, описанную в предыдущем разделе, мы вычисляем положение центра масс и значение матрицы инерции рабочего органа с прикрепленным к нему остатком робота. Затем вычисляется обратная динамика для манипулятора. Вектор крутящих моментов, приложенных к шарнирам, отмечен

---

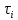, который обобщает уравнения обратной динамики движения робота-манипулятора в виде вектора, записывается следующим образом: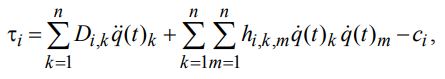



(38)

где 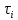– обобщённые силы в i -м сочленении для реализации движения i -го звена, 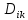определяется формулой (39), устанавливает связь сил и моментов которые действуют в сочленениях с ускорениями присоединённых переменных, 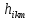– определяется равенством (40) и (41), устанавливает связь сил и моментов, которые действуют в сочленениях со скоростями изменения присоединенных переменных, определяется равенством (42), вычисляет силу тяжести, воздействующую на звенья манипулятора, 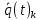– обобщённое ускорение, 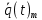– обобщённая скорость, 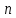– количество звеньев робота-манипулятора.

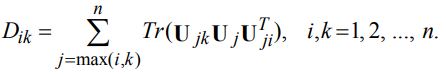Коэффициенты 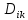определяются равенством
(39)

Коэффициенты 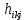определяются равенством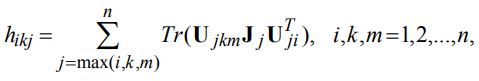




(40)




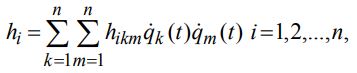
(41)

Где 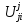– матрица, описывает изменения положения i-го звена, возникающие при движении в j -м сочленении манипулятора; 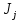– матрица моментов инерции j-го звена; 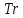– след полученной матрицы. Коэффициенты определяются равенством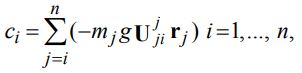

---

(42)

где 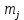– масса j -го звена; – матрица описывает изменения положения i звена, возникающие при движении в j сочленении манипулятора; 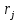– вектор центра масс i звена в собственной системе отсчёта, 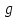– сила тяжести.
5.3 Формулировка обратной динамики в MatLab

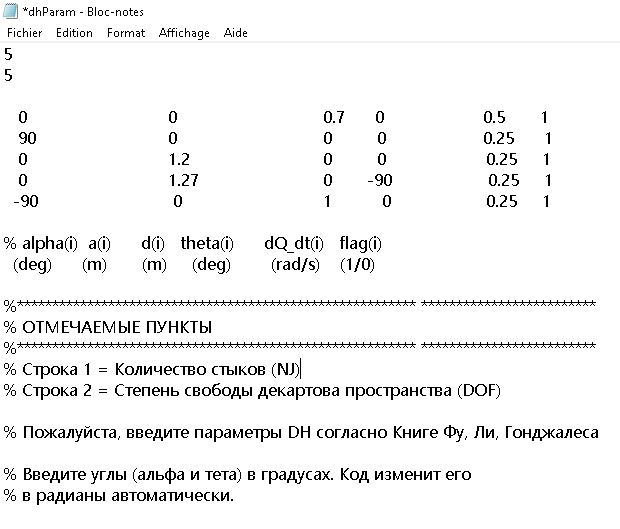
В этой части речь идет о численном решении уравнений руки манипулятора, составляющих вектор крутящих моментов приводов в зависимости от того, является ли соединение ротоидным или призматическим через интерфейс MatLab.

Обратная динамика робота-манипулятора любой степени свободы с использованием динамической формулировки Лагранжа-Эйлера (J. J. Uicker, "On the dynamic analysis of spatial linkages using 4 x 4 matrices," Ph.D. dissertation, Northwestern Univ., Aug. 1965). Входными данными являются переменные суставного пространства (положение сустава, скорость и ускорения), а выходными данными являются крутящие моменты/силы в суставах. Код использует дистальные параметры DH манипулятора. Существует только один входной файл: текстовый файл (dhParam.txt), который получает от пользователя дистальные параметры DH манипулятора, а также необходимо ввести скорости и ускорения суставов.

Структура кода приведена ниже:



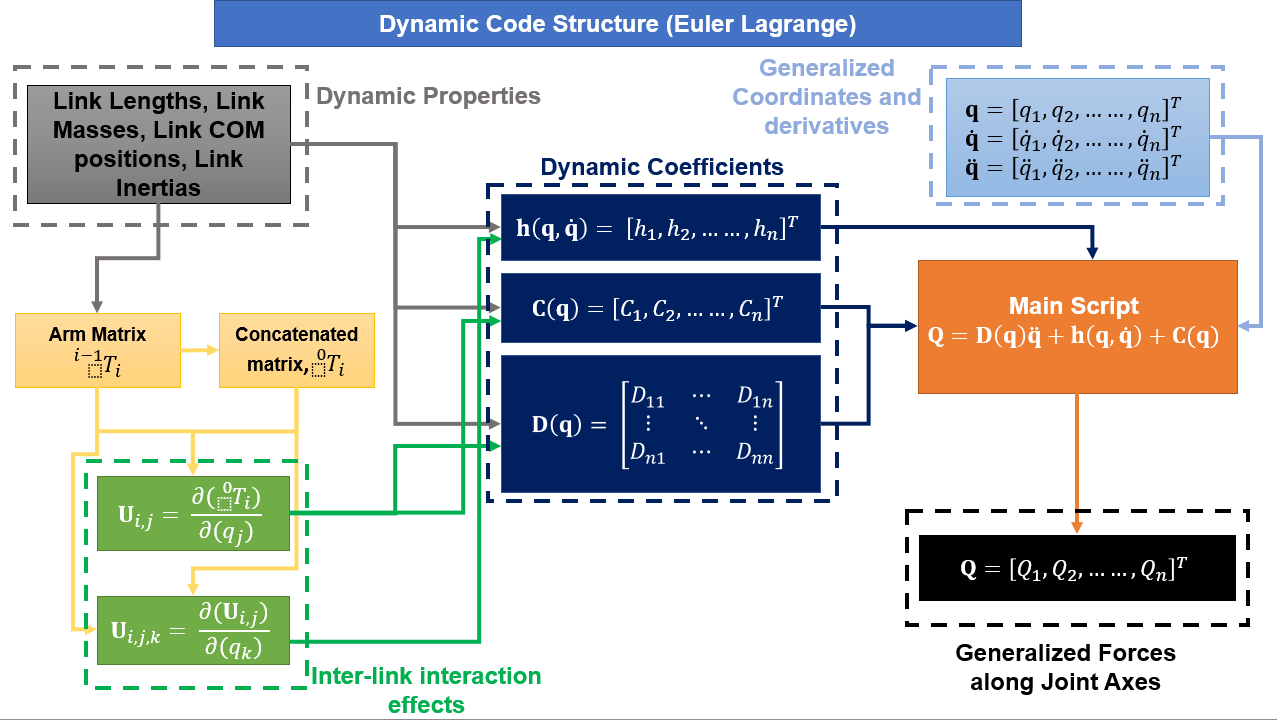
Рис. 11. Динамическая структура кода (Эйлер Лагранж)

Объяснение скриптов, включенных в репозиторий:

1). ArmMatrix.m вычисляет однородные матрицы преобразования от одного кадра к соседнему кадру, в то время как T_Concat.m вычисляет конкатенированную матрицу от начального кадра к конечному кадру.

2). inv_dynamics_Euler_Lagrange.m — это основной скрипт, который необходимо выполнить для вычисления крутящих моментов в суставах. Поскольку это код обратной динамики, выходными данными будут крутящие моменты (в случае вращательных шарниров) и силы (в случае призматических шарниров) вдоль осей шарнира. Формулировка Эйлера-Лагранжа выполняется в матричной форме, где нам нужно вычислить матрицу инерционного ускорения, матрицу центробежной силы и силы Кориолиса, а также матрицу гравитационной нагрузки.

---

3). inertia_acceleration_matrix.m — это функция, которая вычисляет матрицу инерционного ускорения. Каждый член этой матрицы в основном означает реактивный крутящий момент/силу, воздействующую на конкретное соединение/звено из-за ускорения другого соединения/звена. Эта матрица всегда симметрична и положительно определена.

4). centri_cor_force_matrix.m — это функция, которая вычисляет матрицу центробежной силы и силы Кориолиса. Каждый член этой матрицы вычисляет центробежную силу и силу Кориолиса, создаваемую одним шарниром/звеном из-за скорости двух других шарниров/звеньев. Эта матрица является самой затратной в вычислительном отношении, и для приложений с низкими скоростями ею можно пренебречь.

5). gravity_loading_matrix.m — это функция, которая вычисляет матрицу гравитационной нагрузки, каждый член которой соответствует рассмотрению потенциальной энергии каждого звена из-за гравитации.

6). U1_matrix.m — это функция, которая вычисляет влияние на положение и ориентацию конкретного звена из-за движения двух других звеньев. По сути, это матрица. Функция в основном вычисляет все такие возможные матрицы (например, движение 2-го и 3-го суставов в манипуляторе не окажет никакого влияния на положение и ориентацию базового сустава, вместо этого будет наоборот) и группирует их в тензор (матрицу ячеек) и возвращает матрицу ячеек при вызове в основном скрипте.

7). U_matrix.m — это функция, которая вычисляет влияние движения одного звена/соединения на положение и ориентацию другого звена. Он вычисляет матрицу так же, как U1_matrix.m.

8). inertia_matrix.m — это функция, которая вычисляет матрицу/тензор псевдоинерции каждой ссылки в манипуляторе. Момент инерции массы звена рассчитывается по отношению к раме дистального шарнира звена.

Эта формулировка имеет вычислительную сложность 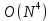, что делает ее вычислительно неэффективной и непригодной для таких приложений, как тестирование конструкции контроллера в реальном времени, хотя это высокоструктурированный алгоритм.

Для выполнения сценария inv_dynamics_Euler_Lagrange.m на нашем манипуляторе с 5 степенями свободы мы должны произвольно выбрать положение манипулятора, определить параметры DH, скорости и тип рычажного соединения (0/1) каждого сустава через файл dhParam.txt. Затем в основном скрипте вводим геометрические характеристики тел нашего робота-манипулятора (Табл. 1).

---

Смотрите также файлы

• Российский государственный социальный университет итоговое практическое задание по дисциплине История социальной работы.docx

• Международная торговля и мировой рынок. Междунар одная торговая политика.pdf

• 1. Строится двоичная запись числа N. В конец записи (справа) дописывается вторая справа цифра двоичной записи.doc

• Доклад по дисциплине Практическая социология.docx

• Программа формирования здорового и безопасного образа жизни воспитанников на 2016 2021 г г.doc