Файл: Контрольная работа по математике Требования к оформлению контрольной работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
контрольная работа по математике
Требования к оформлению контрольной работы
-
Контрольную работу следует выполнить в ученической тетради в клетку. -
Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров m и n, и только после этого приступать к их решению. -
Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра (А — предпоследняя цифра, В — последняя цифра). Значение параметра m выбирается из таблицы 1, а значение параметра n - из таблицы 2. Эти два числа m и n и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра m)
| А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| m | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
Таблица 2 (выбор параметра n )
| В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n | 3 | 5 | 4 | 2 | 1 | 5 | 4 | 1 | 3 | 2 |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что m =4, n =1. Полученные m = 4 и n = 1 подставляются в условия всех задач контрольной работы этого студента.
Контрольная работа
элементы линейной алгебры
-
Решить систему уравнений методом Крамера, Методом Гаусса
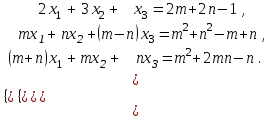
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
-
Дана треугольная пирамида с вершинами в точках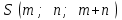 ,
,  ,
, 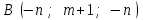 ,
, 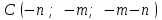 ,. Найти:
,. Найти:-
уравнение плоскости, проходящей через точки А, В и С; -
величину угла между ребром SC и гранью АВС; -
площадь грани АВС; -
объем пирамиды SАВС.
-
КОМПЛЕКСНЫЕ ЧИСЛА
-
Выполнить действия:
а)
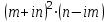 ; б)
; б) 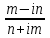 .
.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
-
Найти пределы функций: а)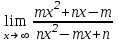 ; б)
; б) 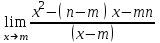 .
.
-
Найти производные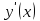 функций: а)
функций: а) 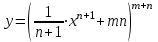 ; б)
; б) 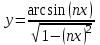 .
.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
-
Найти интегралы: а)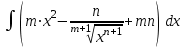 б)
б) 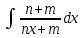 в)
в) 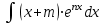
-
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями: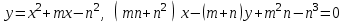 ;
;
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
-
Найти частные производные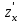 ,
, 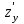 и
и 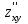 функции
функции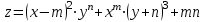 .
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
-
Найти общее решение уравнения:
а)
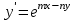 . б)
. б) 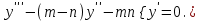
РЯДЫ
-
Исследовать на сходимость ряды с положительными членами:
а)
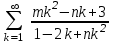 ; б)
; б) 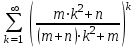 .
.ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
-
В урне находятся m+2 белых, n+2 черных шара. Последовательно извлекаются наудачу 3 шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым. -
Закон распределения дискретной случайной величины X имеет вид:
| xi | -2 | -1 | 0 | m | m+n |
| pi | 0,2 | 0,1 | 0,2 | 0,3 | 0,2 |
Найти математическое ожидание M(X), дисперсию D(X).
-
Выборка Х объемом N=100 измерений задана таблицей

По исходным данным:
-
Построить полигон относительных частот -
Вычислить среднее выборочное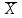 , выборочную дисперсию, среднее квадратическое отклонение
, выборочную дисперсию, среднее квадратическое отклонение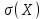 .
.
Пример выполнения контрольной работы см. в учебнике: Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
-
– стр. 115
-
– стр. 127
-
– стр.281 -
– стр. 74
-
– стр. 135, 136
-
– стр.228
-
– стр. 232
-
– стр.237
-
– стр. 243, 249
-
– стр.253–254 -
– стр.351 -
– стр.352–353 -
– стр.359, 360, 328