Лекции по алгебре и геометрии. Семестр 2.

Лекция 19. Алгебра матриц.

Краткое содержание: Основные определения, действия с матрицами и их свойства, нулевая и единичная матрицы, обратная матрица и ее свойства, обратимые матрицы.
Глава 1. Алгебра матриц.

п.1. Основные определения.

Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.
Определение. Матрицей размера над полем К называется таблица элементов поля К, имеющую строк и столбцов.
Обозначение:

.
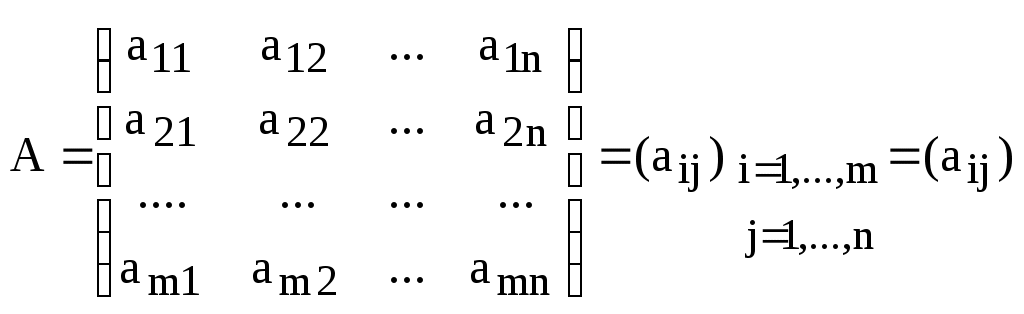Определение. Элементы называются элементами матрицы, где i – номер строки, в которой находится элемент , j – номер столбца.
Определение. Матрица размеров :

называется строкой длины .
Определение. Матрица размеров :

называется столбцом высоты .
Определение. Матрица размеров называется квадратной матрицей – го порядка.
Определение. Матрица, все элементы которой равны нулю, называется нулевой.
В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.

Главную диагональ образуют элементы

---

, т.е. элементы с одинаковыми нижними индексами.

Побочную диагональ образуют элементы .
Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:

.
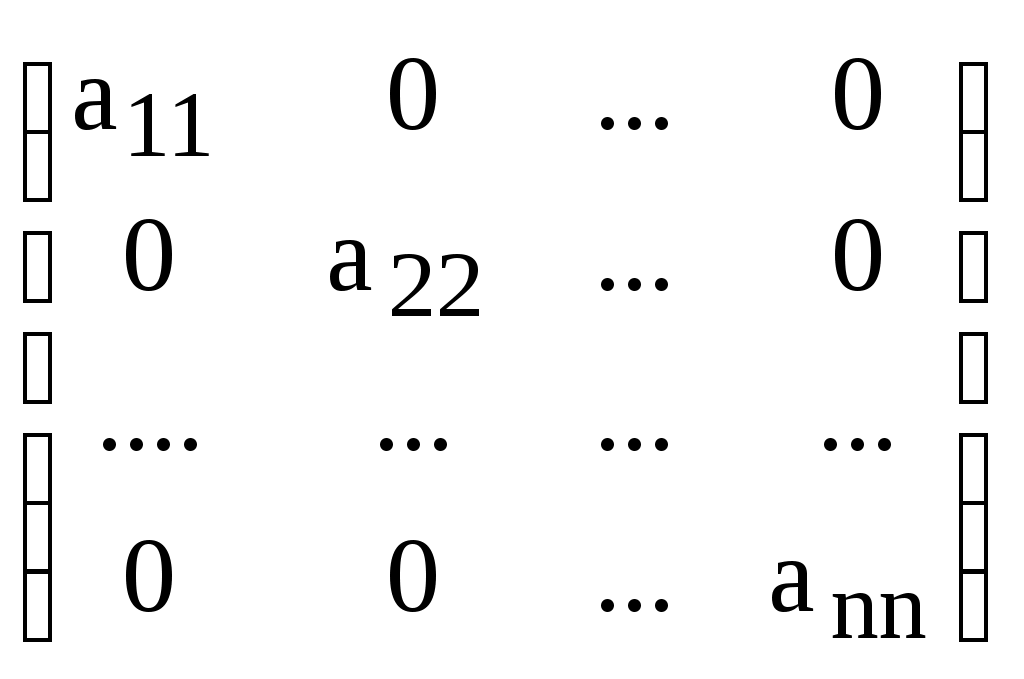Определение. Матрица В размера называется транспонированной по отношению к матрице А размера , если к – й столбец матрицы В состоит из элементов к – й строки матрицы А, для всех .

Обозначение: .
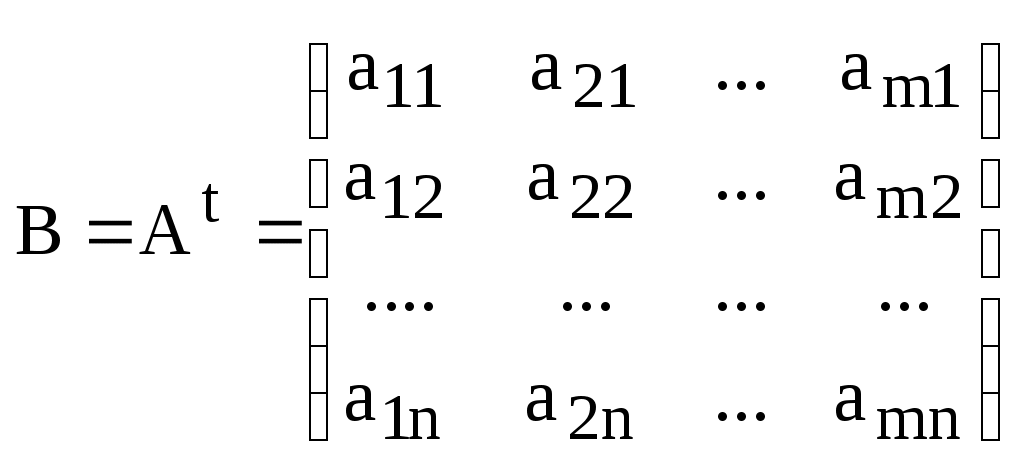Определение. Процесс (процедура) получения транспонированной матрицы из данной называется транспонированием матрицы.
Пример:

, .
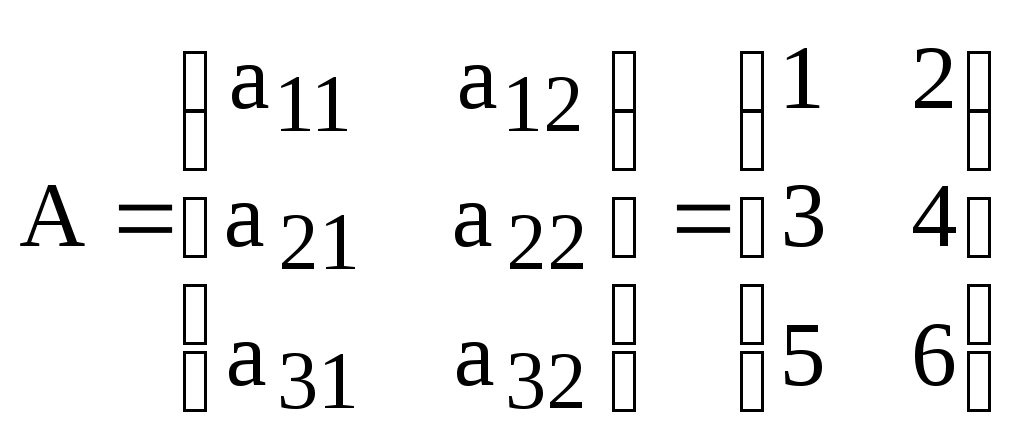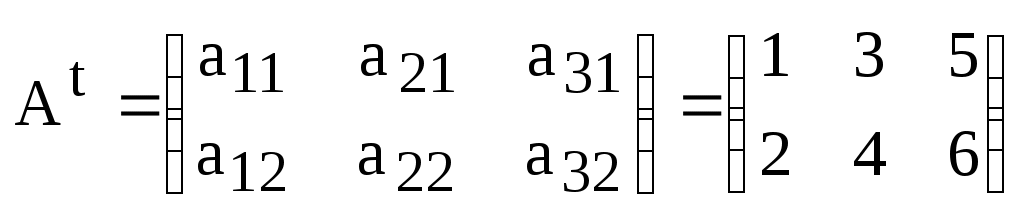Определение. Две матрицы и называются равными, если они имеют одинаковые размеры и для всех значений индексов выполняется равенство .
п.2. Сложение матриц.
Определение. Суммой матриц и одинаковой размерности называется третья матрица такой же размерности , где ее элементы определяются равенством для всех значений индексов.
Обозначение:

---

.

Другими словами, для того, чтобы найти сумму двух матриц одинаковой размерности, нужно сложить соответствующие элементы (т.е. элементы, имеющие одинаковые нижние индексы) этих матриц.

Замечание. Сложение матриц различных размеров не определено. (Их нельзя складывать!)
Пример: , ,

.
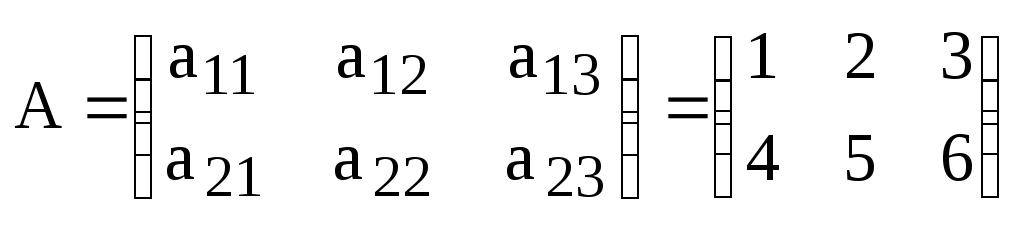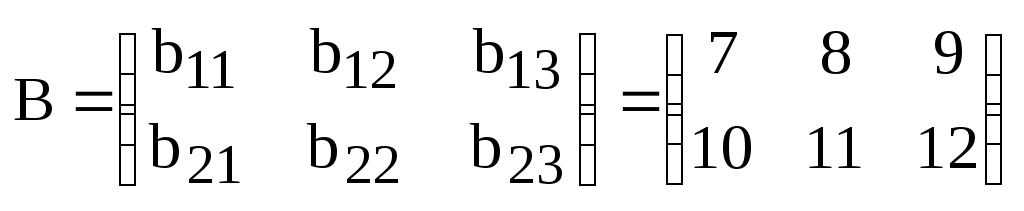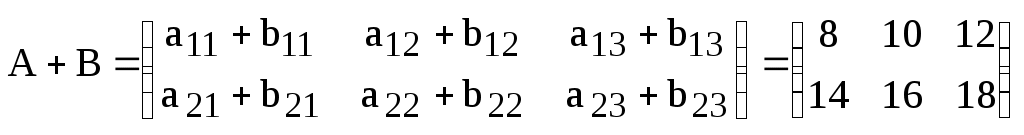Определение. Матрица В называется противоположной матрице А, если она удовлетворяет равенству , где 0 – нулевая матрица.
Обозначение: .
Множество всех матриц размера над полем K обозначим через
Теорема. (Свойства сложения матриц.)

Множество относительно сложения является абелевой группой.
Другими словами, сложение матриц подчиняется следующим законам:

1) ассоциативность: справедливо равенство ;

2) существование нулевой матрицы:

– нулевая матрица, такая, что верны равенства ;

3) существование противоположной матрицы:

, : ;

4) коммутативность:

---

.
п.3. Умножение матрицы на скаляр.

Определение. Произведением скаляра на матрицу называется матрица тех же размеров, что и матрица А, где элементы определяются равенством , для всех значений индексов.
Обозначение: .
Другими словами, для того, чтобы умножить матрицу на скаляр, нужно каждый элемент матрицы умножить на данный скаляр.
Пример:

,

.
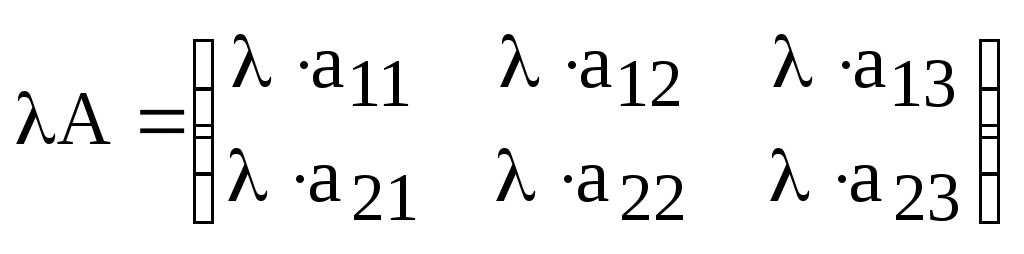Замечание. Легко видеть, что умножив матрицу на (–1) мы получаем противоположную матрицу: .
Теорема. (Свойства умножения матрицы на скаляр.)

Умножение матрицы на скаляр подчиняется законам:

5) ассоциативность: и

;

6) если 1 – единица поля K, тогда

;

7) дистрибутивность умножения относительно сложения скаляров: и

;

8) Дистрибутивность умножения относительно сложения матриц: и

---

.
Следствие. Множество относительно сложения матриц и умножения матриц на скаляр является векторным пространством над полем К.
Обозначим через множество всех столбцов высоты n с элементами из поля K.
Следствие. Множество является векторным пространством над полем K.
Определение. Векторное пространство называется арифметическим векторным пространством столбцов высоты n.

п.4. Умножение матриц.

Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:

.

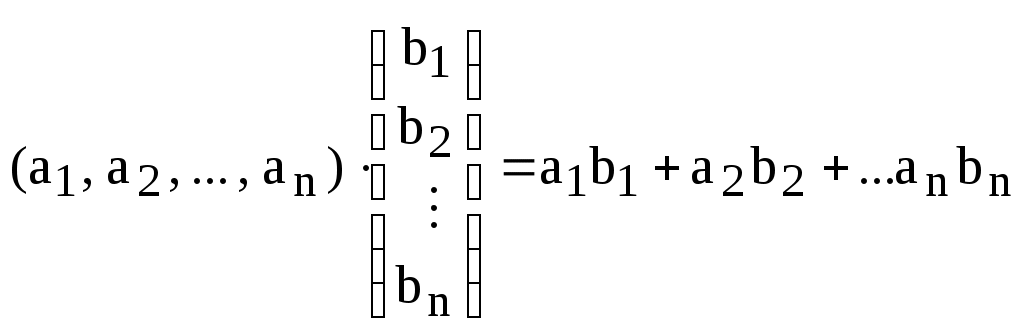Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.
Пример.
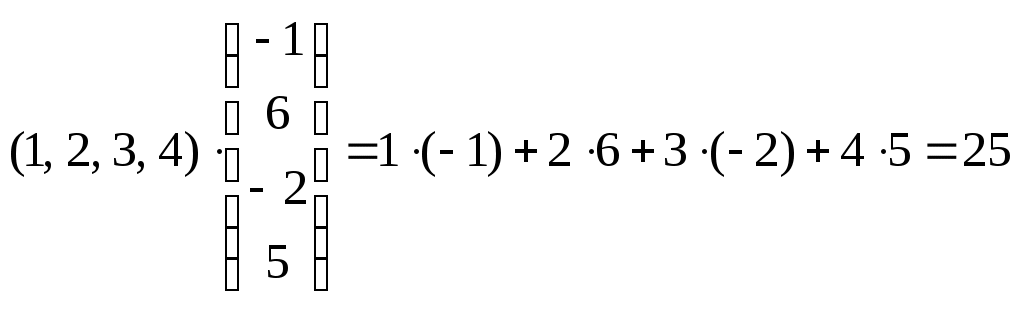
Определение. Произведением матрицы размера на матрицу размера называют матрицу размера , где элемент является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.

---

Смотрите также файлы

• Закон тождества. Сколько времени Без пяти одиннадцать. Шесть, что ли Объясните, почему о казалось возможным двойное понимание ответа.docx

• Отчет по лабораторной работе 16 Часть 3 Вариант 9 студент гр. Ээ4122 Прусаков Матвей.docx

• В какой момент становления психологии, наука смогла выделиться в самостоятельную область.docx

• С. П. Королева (Самарский университет) Юридический институт Кафедра гражданского и предпринимательского права отчет по научноисследовательской работе получение первичных навыков научноисследовательской работы) Упр.pdf

• Что такое конкурентная фирма.docx