ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
или
.Обозначение:
.Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)
Пример.
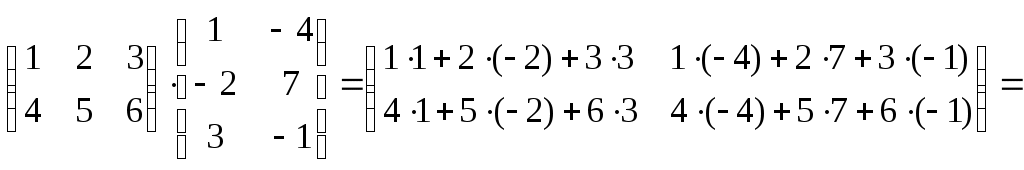
.Определение. Квадратную матрицу
– го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: 
.Множество всех квадратных матриц n-го порядка будем обозначать через
.Теорема. Множество
содержит единичную матрицу n-го порядка, которой является матрица
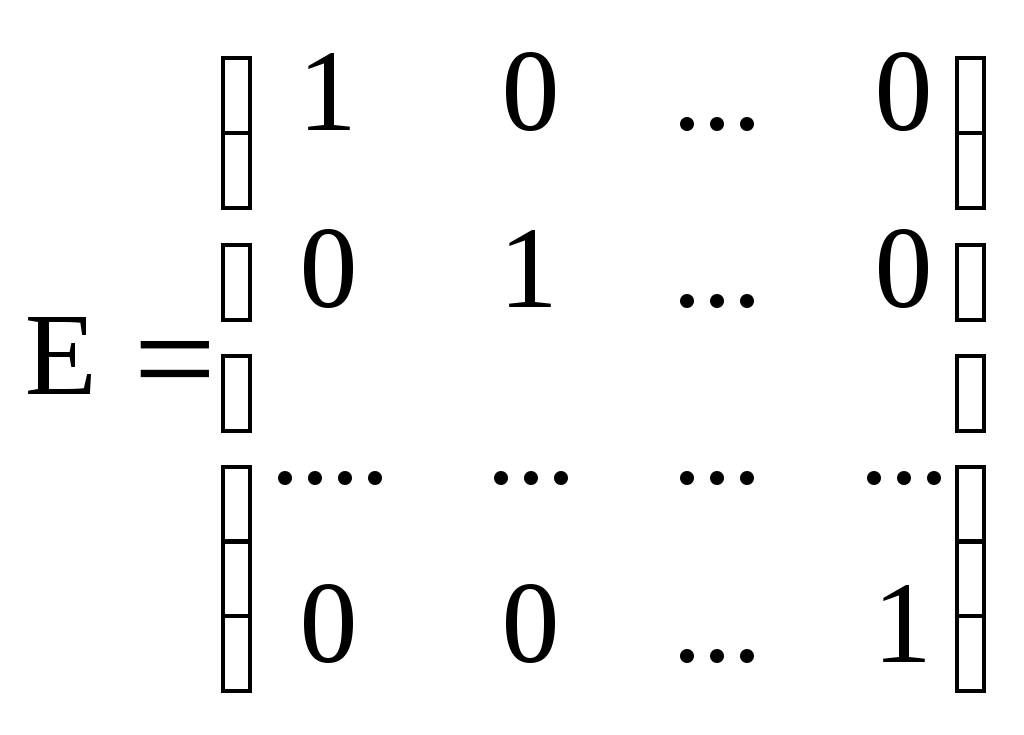.Доказательство этой теоремы предоставляется читателю.
Теорема. Единичная матрица Е является единственной в множестве
.Доказательство. Пусть
еще одна единичная матрица. Тогда, по определению, 
. Положим 
, тогда 
. Далее, по определению, 
. Положим здесь
. Получаем равенство
, отсюда имеем 
, ч.т.д.Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.
Теорема доказана.
Из теоремы следует, что никакая другая матрица, кроме матрицы
не является единичной.Теорема. (Свойства умножения матриц.)
Умножение матриц подчиняется следующим законам:
9) ассоциативность:
;10) существование единичной матрицы:
: 
;дистрибутивность умножения относительно сложения матриц:
11) дистрибутивность умножения относительно сложения матриц:
и 
12) умножение матриц связано с умножением матрицы на число естественным законом:
и 
верно равенство:
.Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.
Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.
Пусть
,
. Тогда 
, 
.Аналогичный пример можно привести для квадратных матриц любого порядка.
Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.
Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.
Доказательство. На множестве
всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо имеет делители нуля.Следствие доказано.
Определение. Натуральной степенью квадратной матрицы А называется матрица
.Нулевую степень квадратной матрицы А
– го порядка по определению полагают равной единичной матрице того же порядка: 
.п.5. Обратная матрица.
Определение. Матрица В называется обратной по отношению к матрице А, если
.Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.
Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.
Определение. Матрица имеющая обратную матрицу называется обратимой.
Теорема. Если квадратная матрица А имеет обратную, то она единственная.
Доказательство. Пусть В и С – две матрицы обратные к матрице А. Тогда
и 
. Имеем,
, ч.т.д.Теорема доказана.
Заметим, что точно также доказывается единственность симметричного элемента в любой полугруппе при условии его существования.
Обозначение: если матрица А обратимая, то обратная к ней обозначается (мы можем это сделать в силу ее единственности) через
.Заметим, что если матрица А обратимая, то обратная к ней матрица
также является обратимой. Обозначение. Множество всех обратимых матриц n-го порядка над полем K обозначается через
.Теорема. (Свойства обратных матриц.)
1. Произведение обратимых матриц одного и того же порядка является обратимой матрицей:
, 
и 
.2. Единичная матрица является обратимой, т.е. если Е – единичная матрица n-го порядка, то
и 
.3. Если А обратимая, то и
также является обратимой, т.е. если 
, то 
и 
.Доказательство. 1) Пусть А и В – обратимые матрицы и
, 
– обратные к ним. Покажем, что произведение
является матрицей обратной к произведению 
:
.Аналогично получаем
. Следовательно, матрица АВ имеет обратную и 
. Отсюда следует, что матрица АВ является обратимой, т.е. 
, ч.т.д.2) Так как
, то по определению, 
, т.е. единичная матрица имеет обратную и, следовательно, единичная матрица является обратимой и 
.3) Действительно, из определения следует, что матрица А является обратной по отношению к матрице
, следовательно, матрица обратимая и 
. Более того, в силу единственности обратной матрицы следует, что
.Теорема доказана.
Следствие. Множество
является некоммутативной группой относительно умножения.Доказательство. На множестве
умножение матриц является внутренней бинарной алгебраической операцией, поэтому осталось лишь проверить аксиомы группы.1) Ассоциативность умножения в множестве
выполняется потому что умножение квадратных матриц ассоциативно (см теорему о свойствах умножения матриц).Далее, в предыдущей теореме доказано, что:
2) единичная матрица