Асинхронные двигатели используются для преобразования электрической энергии в механическую. Однако, примерно в половине исполнительных механизмов промышленности, транспорта и рабочего инструмента используется возвратно-поступательное движение. При этом применяется электропривод, состоящий из обычного асинхронного двигателя с вращающимся полем, редуктора и кинематической передачи, преобразующей вращательное движение в поступательное.

Линейный асинхронный двигатель позволяет исключить из состава электропривода редуктор и кинематическую передачу (кривошипно-шатунный механизм, червячную передачу, систему винт-гайка и т.д.).

Замена двигателя постоянного тока линейным асинхронным двигателем, который имеет намного более простую конструкцию (отсутствие коллектора, вращающихся механизмов, простота изготовления), позволит существенно упростить конструкцию самого станка, отказавшись от применения механического редуктора.

Асинхронный линейный двигатель управляется от транзисторного преобразователя для обеспечения регулировки скорости стола в широких пределах. Частотное регулирование, пуск и торможение относятся к наиболее экономичным методам управления асинхронными двигателями.

В результате достигается экономия по расходу тока, по мощности, по стоимости обслуживания и изготовления, повышается точность и скорость обработки деталей.

1.3 Расчёт цилиндрического линейного асинхронного двигателя
Исходные данные:

- m₁=3;

- F_п = 17600 Н;

- номинальная (средняя) скорость бегуна: V_ном=4 м/мин;

- число полюсов: 2р=6;

- число пазов на полюс и фазу: q=2.

Последовательность расчёта приведена в программе.

Число зубцов бегуна:

Z₁ = 2pm₁q , (1.3)

Z₁= 36.

Средняя скорость:

V_ср = 4 м/мин.

Пазы индуктора и бегуна являются прямоугольными. b_п1 - ширина паза индуктора; b_з1 - ширина зубца индуктора;t₁-зубцовое деление индуктора. Принимается:

<sub>bп1 = 1 см;

bз1 = 0,5 см;

t1 =</sub> b_{п1 +} b_з1 , (1.4)

_{t1 = 1,5 см.}

Находятся основные размеры активной зоны:

Активная длина индуктора:

---

l₁ =t₁Z₁ , (1.5)

l₁ = 54 см.

Выбирается наружный диаметр бегуна из соображений механической прочности с учётом того, что масса бегуна должна быть минимальной. Принимаем:

D₂ = 8 см.

Величину воздушного зазора выбирается из соображений минимума

МДС зазора, но с учётом технологии. Принимается:

δ = 0,15см.

Определяется внутренний диаметр индуктора:

D₁ = D₂+2δ , (1.6)

D₁= 8,3 см.

Выбирается число зубцов бегуна Z₂ с учётом рекомендаций для обычных АД:

Z₂ = 50

Определяется зубцовое деление бегуна:

t₂ = l_I/Z₂ , (1.7)

t₂ = 1,1 см.

Выбирается ширина паза b_п2 и ширина зубца b_з2 бегуна:

b_п2 = 0,78 см;

b_з2 = t₂ – b_п2 , (1.8)

b_з2 = 0,32 см.

Принимается глубина паза бегуна h_п2, высота зубца h_п1 и спинки h_сп1 индуктора:

h_п2= 2,5 см;

h_п1 = 5 см;

h_сп1= 3 см.

Применяется однослойная обмотка. Число эффективных проводов в пазу u_п, диаметр неизолированного проводника d_пр, сечение неизолированного проводника q_пр:

u_п = 40;

d_пр = 3,5 мм.

q_пр = πd_пр²/4 , (1.9)

q_пр = 9,621х10^-6 м².

Вычисляется коэффициент заполнения k_зап:

k_зап = u_пq_пр/b_п1h_п1 , (1.10)

k_зап= 0,77;

k_зап < 0,8.

Вычисляется число витков в фазе (число параллельных ветвей а=1):

W₁ = pqu_п/a , (1.11)

W₁ = 240.

Вычисляется обмоточный коэффициент для однослойной обмотки:

k_об= k_об1 =k_р1.

k_об =0,966.

Таблица 1.2 - Расчет коэффициента Картера k_δ:

Наименование	Формулы	Ответ
Коэффициент Картера по поверхности индуктора	kδ1 = (t1+10δ)/(bз1+10δ)	1,5
Коэффициент Картера по поверхности бегуна	kδ2 = (t2+10δ)/(bз2+10δ)	1,433
Общий коэффициент Картера	kδ = kδ1 kδ2	2,15

_{Таблица}

---

1.3 - Расчет коэффициентов магнитных проводимостей рассеяния

для индуктора λ₁ и бегуна λ₂

Наименование	Формулы	Ответ
1	2	3
Коэффициент магнитной проводимости пазового рассеяния индуктора	λп1 = hп1/3bп1	1,667
Коэффициент магнитной проводимости пазового рассеяния бегуна	λп2 = hп2/3 bп2	0,168
Коэффициент магнитной проводимости дифференциального рассеяния индуктора	λд1 = t1/9.5δ kδ	0,49

1	2	3
Коэффициент магнитной проводимости дифференциального рассеяния бегуна	λд2 = t2/9,5δkδ	0,353
Коэффициент магнитной проводимости рассеяния индуктора	λ1 = λп1 + λд1	2,156
Коэффициент магнитной проводимости рассеяния бегуна	λ2 = λп2+ λд2	1,421

Продолжение таблицы 1.3

Определяется средняя длина витка катушки индуктора:

l_кср = π(D₁+h_п1), (1.12)

l_кср= 41,8 см.

Вычисляется индуктивность катушки индуктора:

L_k1 = u_п²μ_01ксрλ₁ , (1.13)

где μ₀ = 4π10^-7 Гн/м – магнитная постоянная

L_k1 = 1,811 х 10^-3 Гн.

Определяется полюсное деление индуктора:

τ₁= l₁/2p, (1.14)

τ₁= 9 см.

f₁ = V_ср/2τ₁ , (1.15)

f₁ = 0,37 Гц.

Определяется активное сопротивление обмотки индуктора:

r₁ = ρ_м2pqu_пl_кср/q_пр , (1.16)

где ρ_м = 0,0214·10^-6 Ом·м – удельное сопротивление меди при 70˚ С.

r₁ = 0,446 Ом.

Вычисляется сопротивление медного кольца короткозамкнутой обмотки бегуна:

r_мк= ρ_м l_к2/S_к2 , (1.17)

где l

---

_к2 – средняя длина медного кольца бегуна;

S_к2 – площадь паза бегуна

l_к2 = π(D₂-h_п2) , (1.18)

l_к2 = 17,3 см.

S_к2= b_п2h_п2 , (1.19)

S_к2 = 1,95х10^-4м^2.

r_мк = 1,896х10^-5 Ом.

Определяется приведённое активное сопротивления обмотки бегуна:

R_2пр = 4m₁W_1э²r_мк/Z₂ , (1.20)

где W_1э – число эффективных проводников в фазе обмотки индуктора

W_1э = W₁k_об , (1.21)

W_1э = 231,84.

R_2пр = 0,245 Ом.

Находится приведённое индуктивное сопротивление рассеяния обмотки бегуна:

λ_2пр = λ₂Z₁k_об²/Z₂ , (1.22)

λ_2пр = 0,955.

Находится индуктивное сопротивление рассеяние фазы индуктора:

x₁ = 2πf₁N_кфL_к1 , (1.23)

где N_кф – число катушек в фазе индуктора

N_кф = 2pq , (1.24)

N_кф = 12;

x₁= 0,051 Ом.

Вычисляется полное приведённое сопротивление обмотки бегуна:

S = 1, расчёт ведём для пусковой точки.

---

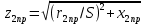
, (1.25)

где x_2пр- приведенное индуктивное сопротивление рассеяния обмотки бегуна

x_2пр = x₁λ_2пр/ λ₁ , (1.26)

x_2пр= 0,022 Ом;
z_2пр = 0,246 Ом;

cosѰ₂ = r_2пр/Sz_2пр , (1.27)

cosѰ₂ = 0,996.

Вычисляется скорость бегущего поля индуктора:

V₁ = 2f₁τ₁ , (1.28)

V₁ = 0,067 м/с.

Находится электромагнитная мощность, передающаяся из индуктора в бегун в пусковом режиме:

Р_12п = F_пV₁ , (1.29)

Р_12п = 1,173х10³ Вт.

Определяется приведённый ток короткозамкнутой обмотки бегуна в пусковом режиме:

I_2ппр = 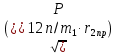, (1.30)

I_2ппр = 39,986 А.

Вычисляется ЭДС обмотки индуктора Е₁=Е_2п:

Е₁ = Р_12п/m₁I_2ппрcosѰ₂ , (1.31)

Е₁ = 9,822 В.

Находится магнитная индукция в воздушном зазоре:

B_δ = Е₁/4,44f₁W_1э²D₁τ₁ , (1.32)

B_δ = 1,724 Тл.

_{Определяется магнитодвижущая сила воздушного зазора:}

F_δ = 2δk_δB_δ/μ₀ , (1.33)

F_δ= 8,851 x10³ А.

Вычисляется магнитный поток в зазоре:

Ф_δ = 2B_δ τ₁D₁ , (1.34)

Ф_δ = 0,026 Вб.

Находится индукция в зубце индуктора:

В_з1 = B_δ t₁/b_з1k_ст , (1.35)

где k_ст=0,93 – коэффициент заполнения зубца индуктора сталью;

В_з1 = 5,563 Тл.

_{Выбирается марка и толщина листа стали для зубцов и сердечников индуктора и бегуна. Определяется напряжённость магнитного поля в зубцах и спинках индуктора и бегуна по кривым намагничивания стали.}

Зубцы индуктора и бегуна и сердечник индуктора изготавливаются из стали 2013 с толщиной листа 0,5 мм. Для сердечника бегуна применяется заготовка из стали Ст10.

Намагниченность магнитного поля в зубце индуктора для стали 2013 при В_з1=5,563Тл: Н_з1=188А/м.

Вычисляется МДС зубцов индуктора:

F_з1 = 2H_з1h_з1 , (1.36)

где h_з1 = h_п1 = 5 см;

F_з1 = 18,8 А.

Вычисляется индукция в спинке индуктора:

---

Смотрите также файлы

• Отчет по лабораторной работе 14 Вариант 9 Выполнил студент гр. Ээ4122 Прусаков Матвей.docx

• Президент Белоруссии Александр Лукашенко рассказал, что переболел аденовирусом Дума приняла закон.docx

• Бухгалтерский учет и анализ движения денежных средств в организации "пао сбербанк".pptx

• Главное Главные новости. Коротко.docx

• Тесты для самоконтроля Задание Какое из этих аналитических выражений является законом Дарси.pdf