Лабораторная работа № 2
Исследование Устойчивости линейных

систем автоматического управления
2.1. Цель работы
Целью настоящей работы является изучение методов исследования и обеспечения устойчивости линейных систем автоматического управления.
2.2. Теоретическая часть
2.2.1. Основные понятия устойчивости линейных систем
Устойчивость – это свойство динамической системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Приведенное понятие устойчивости определяет устойчивость установившегося режима системы. Поэтому можно дать следующее, более общее определение устойчивости: система устойчива, если ее выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений [4].

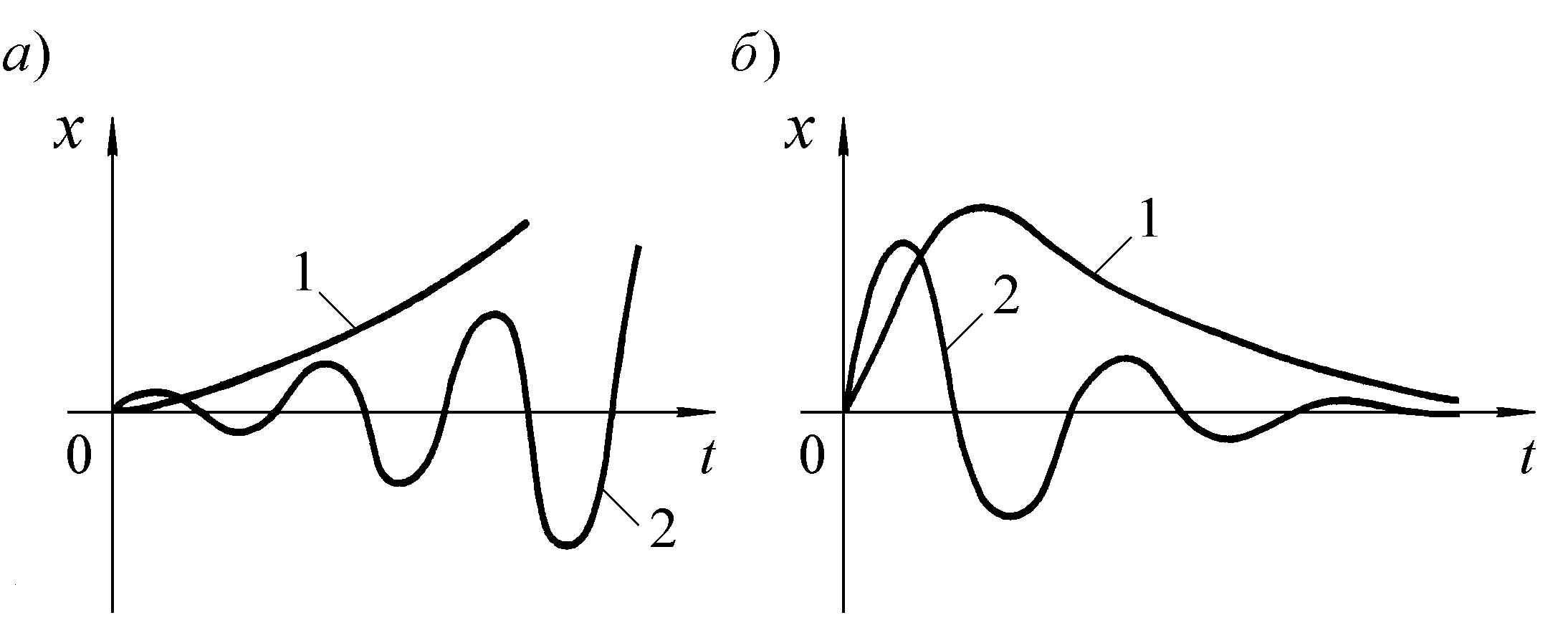
Рис. 2.1. К понятию устойчивости системы
На рис. 2.1 показаны типичные кривые переходных процессов в неустойчивой (а) и устойчивой (б) системах при импульсных возмущениях.

Структурная схема замкнутой системы автоматического управления приведена на рис. 2.2, где 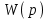– передаточная функция разомкнутой системы

.


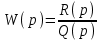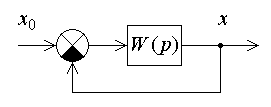
Рис. 2.2. Структурная схема САУ
Дифференциальное уравнение замкнутой системы

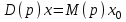, (2.1)

передаточная функция

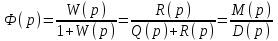, (2.2)

где 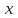– выходная величина; 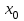– задающее воздействие.

Тогда характеристическое уравнение системы

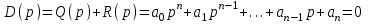. (2.3)

Необходимым и достаточным условием устойчивости линейной системы автоматического управления является отрицательность вещественных частей всех корней ее характеристического уравнения.

Если изобразить корни характеристического уравнения системы точками на комплексной плоскости, то условие устойчивости линейной системы можно сформулировать еще так: условием устойчивости системы является расположение всех корней характеристического уравнения, т.е. полюсов передаточной функции системы, в левой комплексной полуплоскости или, короче, все они должны быть левыми.

---

В теории автоматического управления пользуются условиями, которые позволяют судить о расположении корней в левой полуплоскости без нахождения их значений. Эти условия называются критериями устойчивости. Существующие критерии устойчивости делятся на две группы: алгебраические и частотные критерии.
2.2.2. Алгебраические критерии устойчивости
Условия устойчивости в алгебраических критериях сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме алгебраический критерий Рауса-Гурвица был предложен английским математиком Е. Раусом, а затем швейцарским математиком А. Гурвицем в 19 веке. Приведем без доказательства этот критерий в форме Гурвица [4].

Возьмем характеристический полином, определяющий левую часть дифференциального уравнения системы,

,

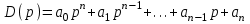где полагаем 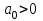, что всегда можно обеспечить умножением при необходимости полинома на 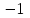. Составим из коэффициентов этого полинома определитель

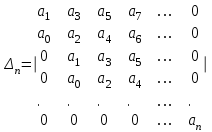. (2.4)

Этот определитель называется определителем Гурвица. Он имеет 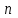строк и 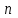столбцов. Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется до положенного числа 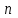элементов нулями. Вторая строка включает все четные коэффициенты и также заканчивается нулями. Третья строка получается из первой, а четвертая – из второй сдвигом вправо на один элемент. На освободившееся при этом место ставится нуль. Аналогично сдвигом вправо на элемент получаются все последующие нечетные и четные строки из предыдущих одноименных строк.

В результате в главной диагонали определителя оказываются последовательно все коэффициенты кроме .

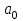Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров:

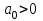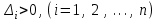; . (2.5)

Развернем критерий Гурвица для нескольких конкретных значений

---

.

Для



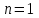
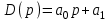
и условия устойчивости сводятся к неравенствам

; .

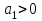Для



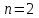
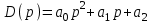
и условия устойчивости сводятся к неравенствам

; ; .

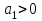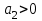Для



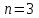
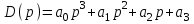
и условия устойчивости сводятся к неравенствам

; ; ; ;

.

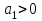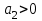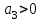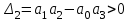В общем случае системы -го порядка можно показать, что в условия устойчивости в качестве их части входит требование положительности всех коэффициентов уравнения, что является необходимым условием устойчивости.

Можно показать, что если выполнены все условия критерия Гурвица, кроме одного 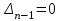, то характеристическое уравнение системы имеет пару сопряженных чисто мнимых корней. Если же выполнены все условия Гурвица, кроме одного 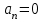, то уравнение имеет один нулевой корень. И в одном, и в другом случае система находится на границе устойчивости: в первом случае она называется границей колебательной устойчивости, а во втором – апериодической устойчивости [3].

---

2.2.3. Частотные критерии устойчивости
Принцип аргумента. В основе частотных критериев устойчивости лежит известный в теории функций комплексного переменного принцип аргумента [2, 3].

Пусть дано алгебраическое уравнение с действительными коэффициентами

.

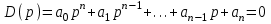Многочлен 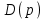можно представить в виде

,

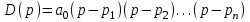где 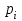– корни уравнения .

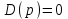Положим , тогда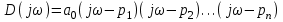

.

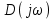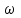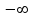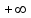Изменение аргумента комплексного числа при изменении в пределах от до равно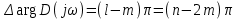

, (2.6)

где 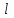– число корней в левой и 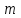– число корней в правой полуплоскости комплексной плоскости.

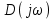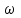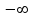Таким образом, принцип аргумента формулируется следующим образом. Изменение аргумента при изменении от до 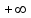равно разности между числом корней 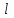уравнения 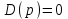, лежащих в левой полуплоскости, и числом корней 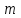лежащих в правой полуплоскости, умноженной на .

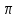Критерий Михайлова. Критерий устойчивости А.В. Михайлова, сформулированный им в 1938 г., является по существу геометрической интерпретацией принципа аргумента [2].

---

Пусть дано характеристическое уравнение системы

.

Для того чтобы система была устойчива, необходимо, чтобы все корни характеристического уравнения лежали в левой полуплоскости, т.е. чтобы 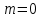. В этом случае должно удовлетворяться условие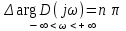



или

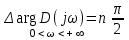. (2.7)

Геометрическое место конца вектора при изменении от 0 до называется годографом вектора , или годографом Михайлова.

Отсюда следует формулировка критерия устойчивости Михайлова. Система автоматического управления устойчива, если годограф с ростом от 0 до , начинаясь на действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) квадрантов, где – порядок характеристического уравнения.

На рис. 2.3 показаны типичные годографы Михайлова для устойчивых систем, описываемых уравнениями от первого до пятого порядка.

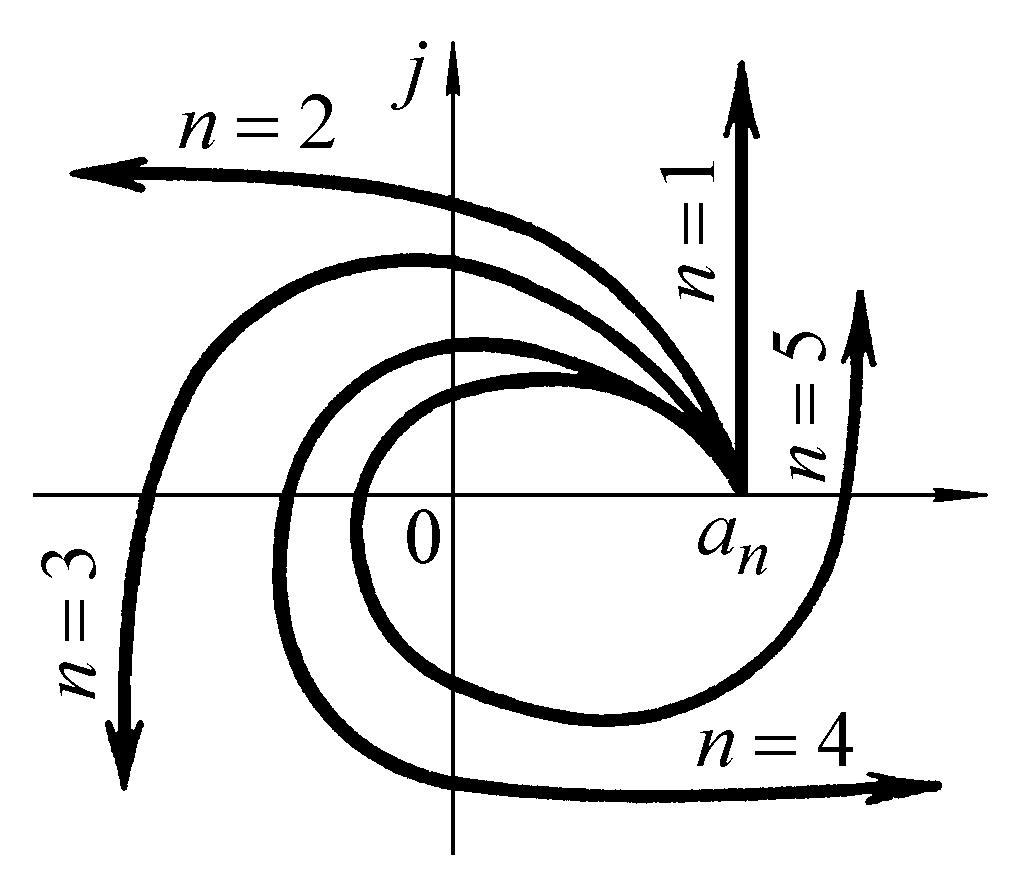
Рис. 2.3. Годографы Михайлова для устойчивых систем
Критерий Найквиста. Этот критерий устойчивости был предложен Г. Найквистом (1932 г.) для исследования устойчивости усилителей с обратной связью [3].

Для исследования устойчивости замкнутой системы управления согласно этому критерию необходимо знать амплитудно-фазовую частотную характеристику (частотный годограф) разомкнутой системы, которую можно получить как аналитически, так и экспериментально.

Пусть передаточная функция разомкнутой системы

.

Подставляя в это выражение

---

Смотрите также файлы

• Решение которой прикрепляете в задание решение практических задач (3 семестр).docx

• C. Акантолизис.pdf

• Теоретические аспекты формирования и развития команды проекта для создания медиапродуктов.pdf

• Английский язык в жизни судоводителя.docx

• Сочинения в конце каждого урока. Пока не все, но пополняются регулярно, заходите почаще. Как только закончу работу над всеми уроками онлайн, помещу сочинения на отдельной странице).docx