2. По заданной структурной схеме определить передаточную функцию замкнутой системы. Определить область устойчивости методом D-разбиения.

3. Провести моделирование заданной линейной системы. Используя алгебраические и частотные критерии устойчивости, определить устойчивость и запасы устойчивости.
2.4. Описание лабораторной установки
Лабораторной установкой является ЦВМ IBM PC для проведения цифрового моделирования.

Цифровое моделирование переходных процессов и частотных характеристик линейных систем автоматического управления производится с использованием пакетов Control и Simulink системы Matlab [6-8].

В этой работе исследуется влияние параметров системы автоматического управления на устойчивость и на показатели качества переходного процесса.

Для исследования предлагается система автоматического управления летательного аппарата (ЛА) по углу крена 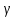, функциональная схема которой приведена на рис. 2.7. Она состоит из измерительного устройства – гировертикали (ГВ), которая выдает сигнал 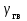, пропорциональный углу крена 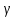. При появлении отклонения от заданного угла крена 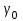: 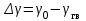усилитель (У) подает сигнал 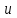на вход сервопривода (СП) элеронов. Сервопривод поворачивает элероны летательного аппарата (ЛА) на угол 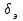так, чтобы скомпенсировать отклонение угла крена 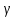от заданного угла крена 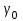. При задании команды на изменение угла крена 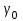, система управления изменит значение угла крена ЛА так, чтобы отклонение 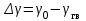стремилось к нулю.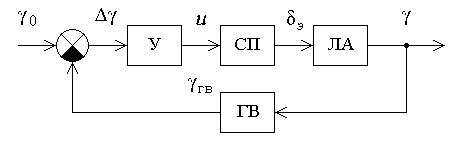

Рис. 2.7. Функциональная схема САУ углом крена ЛА
Звенья системы управления описываются следующими уравнениями:

---

1. Измерительное устройство – гировертикаль

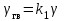; (2.11)

2. Усилитель

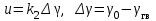; (2.12)

3. Сервопривод

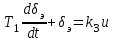; (2.13)

4. Летательный аппарат

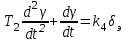. (2.14)

Параметры звеньев системы приведены в таблице.

Вариант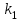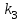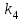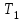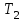
1	1	4	5	0,1	1
2	1	2	4	0,2	1,2
3	1	1	3	0,3	1,4
4	1	0,5	2	0,4	1,6
5	1	0,25	1	0,5	1,8

В таблице даны значения всех параметров звеньев, кроме коэффициента передачи вычислителя 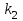. Надо выбрать коэффициент передачи вычислителя 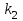из условия устойчивости замкнутой системы.

Пример программы моделирования данной системы в пакете Control системы Matlab для случая единичных параметров звеньев приведен в приложении 2.

Схема моделирования системы с использованием пакета Simulink системы Matlab для случая единичных параметров звеньев приведена на рис. 2.8.

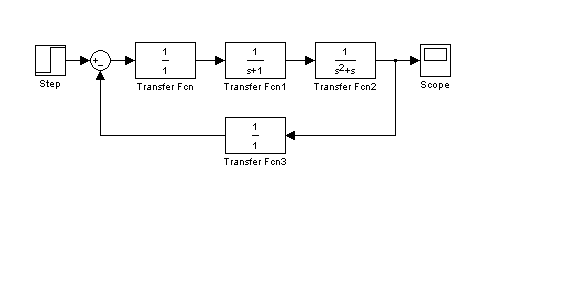
Рис. 2.8. Схема моделирования САУ углом крена ЛА
Параметры летательного аппарата задаются с помощью блока Transfer Fcn2, параметры сервопривода – с помощью блока Transfer Fcn1, параметры усилителя – с помощью блока Transfer Fcn, параметры гировертикали – с помощью блока Transfer Fcn3.

---

Входным сигналом САУ является единичное ступенчатое изме-нение – блок Step. На выходе схемы с помощью блока Scope наблюдается переходной процесс по выходной координате системы .
2.5. Порядок выполнения работы
Задание 1. Изучение основных положений теории устойчивости линейных САУ
1. Изучить основные определения, необходимые и достаточные условия устойчивости.

2. Изучить критерии устойчивости линейных систем.

3. Изучить метод D-разбиения по одному параметру системы.
Задание 2. Анализ устойчивости САУ углом крена ЛА
1. По дифференциальным уравнениям определить передаточные функции звеньев и передаточную функцию замкнутой системы.

2. Определить характеристическое уравнение замкнутой системы.

3. Построить границу D – разбиения в зависимости от коэффициента усиления .

4. Выбрав значение из внутренней области D – разбиения, проверить устойчивость замкнутой системы по критерию Гурвица.
Задание 3. Моделирование САУ углом крена ЛА
1. Составить программу моделирования САУ в пакете Control системы Matlab

2. Составить схему моделирования САУ в пакете SimuLink системы Matlab.

3. Определить устойчивость системы по критериям Михайлова, Найквиста, построить логарифмические частотные характеристики разомкнутой системы и определить запасы устойчивости по амплитуде и по фазе.

4. Построить переходную функцию и определить показатели качества переходной функции при различных значениях коэффициента .
2.6. Требования к отчету
Отчет по работе должен содержать:

1. Цель работы;

2. Структурные схемы;

3. Результаты расчетов;

4. Результаты моделирования;

5. Выводы.

По заданию 1 в отчёте приводятся функциональная и структурная схемы САУ, основные положения теории устойчивости систем.

По заданию 2 в отчете приводятся результаты вывода передаточных функций, характеристическое уравнение системы и расчет коэффициента с помощью метода D – разбиения.

По заданию 3 в отчёте приводятся полученные графики частот-ных и временных характеристик системы, их анализ.

---

2.7. Контрольные вопросы
1. Как определяется передаточная функция замкнутой системы?

2. Дайте определение устойчивости системы автоматического управления.

3. Как определить характеристическое уравнение системы?

4. Как влияет расположение корней характеристического уравнения на устойчивость системы?

5. Как определить устойчивость системы по критерию Гурвица?

6. Как определить устойчивость линейных систем по частотным критериям?

7. Как определить запасы устойчивости по амплитуде и по фазе?

8. Как построить области устойчивости в плоскости одного параметра?

9. Как производят разметку областей устойчивости?

---

Смотрите также файлы

• Решение которой прикрепляете в задание решение практических задач (3 семестр).docx

• C. Акантолизис.pdf

• Теоретические аспекты формирования и развития команды проекта для создания медиапродуктов.pdf

• Английский язык в жизни судоводителя.docx

• Сочинения в конце каждого урока. Пока не все, но пополняются регулярно, заходите почаще. Как только закончу работу над всеми уроками онлайн, помещу сочинения на отдельной странице).docx