Файл: Отчет по лабораторной работе 2 по дисциплине Системы поддержки принятия решений.docx
Добавлен: 29.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Негосударственное образовательное частное
учреждение высшего образования
«Московский финансово-промышленный университет «Синергия»
Факультет информационных технологий
Отчет по лабораторной работе №2
по дисциплине
«Системы поддержки принятия решений»
| Выполнил: | Проверил: | |
| Минин А.Е. (Ф.И.О. студента) | Гумеров Э.А. (Ф.И.О преподавателя) | |
| ДМП-101УЦП (№ группы) | ______________ (оценка) | |
| _______________ (дата сдачи) | ______________ (дата проверки) | |
| Подпись:________________ | Подпись:_______________ | |
Москва – 2022
Исходные данные
Предприниматель желает приобрести автомобиль. Имеются 4 варианта покупки A,B,C и D. В качестве критериев выступают: Цена (К1), Комфортность (К2) и Экономичность (К3). Оценки парных сравнений альтернатив по каждому критерию и критериев между собой имеют вид:
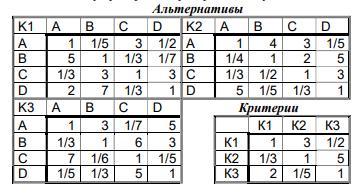
Ход выполнения
Исходные данные
Альтернативы:
| К1 | A | B | C | D |
| A | 1 | 1/5 | 3 | 1/2 |
| B | 5 | 1 | 1/3 | 1/7 |
| C | 1/3 | 3 | 1 | 3 |
| D | 2 | 7 | 1/3 | 1 |
| К2 | A | B | C | D |
| A | 1 | 4 | 3 | 1/5 |
| B | 1/4 | 1 | 2 | 5 |
| C | 1/3 | 1/2 | 1 | 3 |
| D | 5 | 1/5 | 1/3 | 1 |
| К3 | A | B | C | D |
| A | 1 | 3 | 1/7 | 5 |
| B | 1/3 | 1 | 6 | 3 |
| C | 7 | 1/6 | 1 | 1/5 |
| D | 1/5 | 1/3 | 5 | 1 |
Критерии:
| Критерии | |||
| | К1 | К2 | К3 |
| К1 | 1 | 3 | 1/2 |
| К2 | 1/3 | 1 | 5 |
| К3 | 2 | 1/5 | 1 |
Рассчитаем собственный и весовой вектор для каждой группы альтернатив и их критериев.
Таблица 1 – Матрица сравнений уровня важности критериев и их весовые коэффициенты (
| К1 | A | B | C | D | Собственный вектор | Весовой вектор |
| A | 1 | 1/5 | 3 | 1/2 | 0,08 | 0,04 |
| B | 5 | 1 | 1/3 | 1/7 | 0,06 | 0,03 |
| C | 1/3 | 3 | 1 | 3 | 0,75 | 0,37 |
| D | 2 | 7 | 1/3 | 1 | 1,17 | 0,57 |
| Сумма | 2,05 | 1 | ||||
Пример расчета:
Собственный вектор (А) = (1*(1/5)*3*(1/2))^1/4 = 0,08
Сумма собственных векторов = 2,05
Весовой вектор (А) = 0,08/2,05 = 0,04
Рассчитаем для остальных альтернатив:
| К2 | A | B | C | D | Собственный вектор | Весовой вектор |
| A | 1 | 4 | 3 | 1/5 | 0,60 | 0,42 |
| B | 1/4 | 1 | 2 | 5 | 0,63 | 0,44 |
| C | 1/3 | 1/2 | 1 | 3 | 0,13 | 0,09 |
| D | 5 | 1/5 | 1/3 | 1 | 0,08 | 0,06 |
| Сумма | 1,43 | 1 | ||||
| К3 | A | B | C | D | Собственный вектор | Весовой вектор |
| A | 1 | 3 | 1/7 | 5 | 0,54 | 0,25 |
| B | 1/3 | 1 | 6 | 3 | 1,50 | 0,69 |
| C | 7 | 1/6 | 1 | 1/5 | 0,06 | 0,03 |
| D | 1/5 | 1/3 | 5 | 1 | 0,08 | 0,04 |
| Сумма | 2,18 | 1,00 | ||||
Аналогично рассчитаем для критериев:
| Критерии | Собственный вектор | Весовой вектор | |||
| | К1 | К2 | К3 | ||
| К1 | 1 | 3 | 1/2 | 1,14 | 0,37 |
| К2 | 1/3 | 1 | 5 | 1,19 | 0,39 |
| К3 | 2 | 1/5 | 1 | 0,74 | 0,24 |
| Сумма | 3,07 | 1,00 | |||
Лучшей альтернативой считается альтернатива с максимальным значением глобального приоритета.
Пример расчета глобальной альтернативы для К1:
0,37 * 0,04 + 0,39 * 0,03 + 0,24 * 0,25 = 0,23
Рассчитаем аналогично для остальных альтернатив:
| К1 | 0,23 |
| К2 | 0,80 |
| К3 | 0,18 |
| К4 | 0,57 |
| К наилучш | 0,80 |
Таким образом, наилучшей альтернативой будет Альтернатива №2 (К2).
Ответ: Альтернатива №2 (К2).