4. Проверка подшипников на долговечность

4.1. Определение реакций в опорах

Вектор силы полного давления зуба шестерни на зуб ведомого колеса F_nнаправлен по нормали к образующей поверхности зуба [7, с. 306]. Длякосозубой передачи этот вектор (рис.11)представляет собой диагональ параллелепипеда, сторонами которого являются три составляющие силы по трем взаимно перпендикулярным направлениям: F_a, F_rиF_t.В прямозубой передаче осевая сила отсутствует, и сила давления на колесо – это диагональ параллелограмма со сторонамиF_rи F_t.



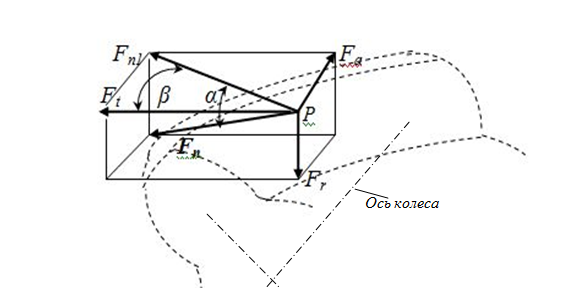
Рис. 11. Силы, действующие в зацеплении косозубой передачи.

Окружная сила: F_t= 2Т/d,

где Т – крутящий момент, d – диаметр делительной окружности

зубчатого колеса.

Осевая сила F_a = F_t·tgβ.

Радиальная сила F_r=F_t·tgα /cosβ.

Определение реакций опор цилиндрической косозубой передачи рассмотрим на примере быстроходного вала. Для этого необходимо построить расчетную схему, как показано на рис. 12.

Реакции находим, пользуясь обычными уравнениями статического равновесия, известными из курса теоретической механики. Изобразив систему координат, реакции раскладываем на составляющие в горизонтальной плоскости XOZив вертикальной плоскости УOZ.



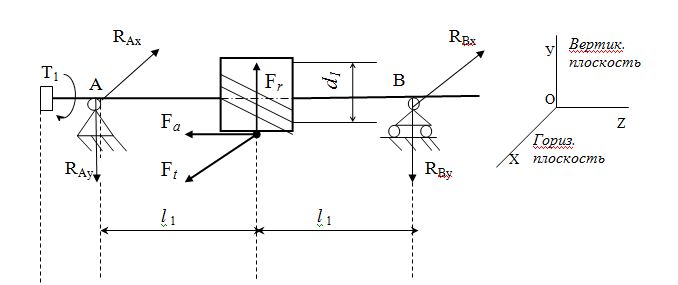
Рис. 12.Расчетная схема для определения реакций в опорах

Уравнения равновесия в горизонтальной плоскости

ΣM_B = -R_AX∙2l₁ +F_t∙l₁ = 0; R_AX = F_t/2.

ΣX = -R_AX - R_BX + F_t= 0; R_BX = F_t - R_AX = F_t /2.

Уравнения равновесия в вертикальной плоскости

ΣM_B = R_Ау∙2l₁ -F_а∙d₁/2 - F_r∙l₁ = 0; R_Ау=F_r/2 + F_а∙d₁ / 4

---

l₁.

ΣM_А = - R_Ву∙2l₁ -F_а∙d₁/2 + F_r∙l₁ = 0; R_Ву=F_r/2 - F_а∙d₁ / 4l₁ .

Равнодействующие реакции находим, как геометрическую сумму:

;

В нашем примере (опоры расположены симметрично) реакциив горизонтальной плоскости равны, а в вертикальной – более нагружена опораА, в сторону которой направлена осевая сила. При несимметричном расположении опор от полюса зацепления могут быть другие соотношения.

4.2. Расчетная долговечность подшипников

Расчет производим по быстроходному валу. Требуемая долговечность подшипника в часах L_hопределяется по эквивалентной нагрузке Р_экв и должна находиться в пределах [L_h]_min≤L_h≤[L_h]_max. Для подшипниковых опор зубчатых передач эти пределы соответствуют 10000…36000 часов работы.

1) . Определяем эквивалентную нагрузку Р_эквпо формуле [2, с.212]

Р_экв= (V∙X∙R_r+Y∙R_a)∙K_Б∙К_Т ,

где V – коэффициент, учитывающий вращение колец: при вращении внутреннего кольца V = 1, при вращении наружного V = 1,2.

X ,Y – коэффициенты радиальной и осевой нагрузки.

- для прямозубой передачи: X= 1; Y = 0;

- для косозубой передачи: X=0,56. Для того чтобы найти значение Y следует вычислить соотношение между осевой и радиальной силой по формуле

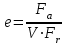, после чего принять Y из таблицы [3, с.195 - 201]

е	0,19	0,22	0,26	0,28	0,30	0,34	0,38	0,42	0,44
Y	2,30	1,99	1,71	1,55	1,45	1,31	1,15	1,04	1,00

---

K_Б – коэффициент динамичности[1,с.115-116].

Для зубчатых передач, редукторов, механизмов поворота и передвижения крановых тележек и т.п. (умеренные толчки, кратковременные перегрузки до 150% от номинальных, вибрации) K_Б = 1,3…1,5.

К_Т – температурный коэффициент [1,с.115]. Принимается в зависимости от рабочей температуры подшипника. Если t_раб ≤ 100^о,то К_Т = 1,0.

R_r - радиальная нагрузка, кН; принимается равной наибольшей величине реакции в опорах (R_AилиR_Bв зависимости от того, какой из подшипников нагружен больше).

Если передача прямозубая и опоры расположены симметрично, тоR_r = R_A=R_B.

R_a – осевая нагрузка на подшипники, кН. В прямозубых передачах R_a = 0;
в косозубых передачах R_a = F_a.

2). Определяем долговечность подшипника в миллионах оборотов

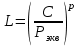, гдеС–динамическая грузоподъемность по каталогу, кН;

р – показатель степени: для шарикоподшипников р= 3;

для роликоподшипников р = 10/3.

3). Номинальная долговечность в часах

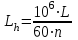, где n – частота вращения кольца подшипника

(число оборотов вала-шестерни).

Если расчетная долговечность подшипника меньше допустимого значения, то следует перейти к более тяжелой серии (например, от легкой к средней). Если долговечность больше максимального значения, то подшипник недогружен; рекомендуется по возможности перейти к более легкой серии.

Если вычисленный ресурс (долговечность) подшипников шариковых и радиальных с цилиндрическими роликами значительно выше, чем каталожное значение, даже для легкой серии, то диаметр вала не следует уменьшать, т.к. он определен из расчета на прочность.

Расчетная долговечность в этом случае будет превышать регламентированную.

5. Проверочный расчет валов и соединений

---

5.1.Построение эпюр изгибающих и крутящих моментов. Определение эквивалентного момента.

Под действием внешних сил, реакций в опорах и моментах в сечениях вала возникают внутренние крутящие и изгибающие моменты. Таким образом, вал испытывает сложную деформацию – изгиб с кручением. Как известно из курса «Сопротивление материалов» расчет вала на прочность можно выполнять на основании принципа независимости действия сил. В этом случае необходимо определить напряжения от каждой силы или момента, после чего рассчитать эквивалентный момент, согласно третьей теории прочности [6, с.275-276].




;

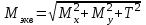
М_x – изгибающий момент в горизонтальной плоскости;

М_y - изгибающий момент в вертикальной плоскости;

Т – крутящий момент.

Далее можно вычислить эквивалентное напряжение для круглых валов

Ϭ_экв= М_экв/ W ≤ [Ϭ],

где W – осевой момент сопротивления изгибу.

[Ϭ] – допускаемое напряжение на изгиб.

При этом расчет ведут как для изгиба (без кручения), но не по изгибающему,
а по эквивалентному моменту.

Для определения эквивалентного момента строим эпюры внутренних крутящих моментов, а также эпюры изгибающих моментов в горизонтальной и вертикальной плоскости(рис.13). Пример дан для косозубой передачи; если в Вашем индивидуальном задании передача прямозубая, то обратите внимание на то, какие силы действуют в зацеплении, есть ли там осевая сила.

При построении эпюр следует использовать свои расчетные значения, а не копировать рисунок, приведенный в методических указаниях !!!
1). Вал-шестерня.

На входном участке вала от полумуфты до полюса зацепления действует постоянный вращающий момент

---

Т₁. При зацеплении шестерни с зубчатым колесом крутящий момент передается на колесо, и далее посредством шпоночного соединения – на тихоходный вал. Поэтому внутренний крутящий момент на участке от полюса зацепления до опорыВравен нулю.

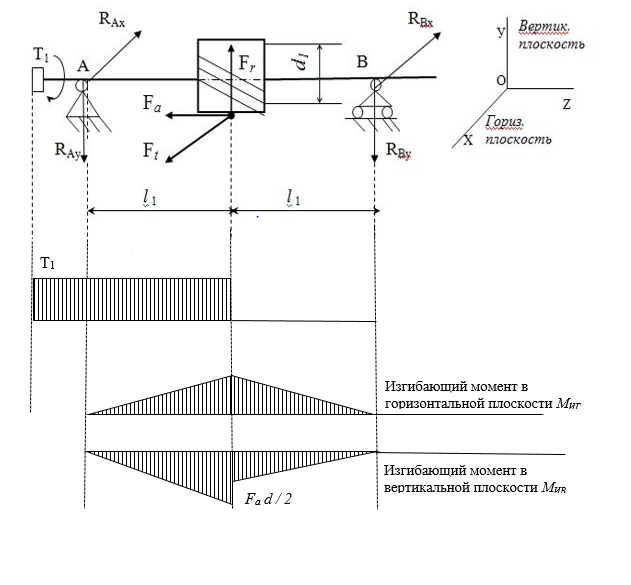
Рис.13. Построение эпюр крутящего и изгибающих моментов на быстроходном валу
Изгибающий момент в горизонтальной плоскости:

- на участке от опорыА до точки зацепления (слева от сечения) эпюра изгибающего момента строится по уравнению:

М_ИГ =R_Aх ∙ z ; где 0 ≤ z≤ l₁

Приz = 0 М_ИГ =0;приz = l₁М_ИГ= F_t∙l₁ / 2.

-на участке от опорыВ до точки зацепления (справа от сечения):

М_ИГ=R_Вх∙ z ; где 0 ≤ z ≤ l₁

Приz = 0 М_ИГ =0;приz = l₁М_ИГ= F_t∙l₁ / 2.

Изгибающий момент в вертикальной плоскости:

- на участке от опоры А до точки зацепления (слева от сечения)

М_ИВ = R_Aу ∙ z ;где 0 ≤ z ≤ l₁

Приz = 0 М_ИВ =0; при z = l₁М_ИВ= F_r∙l₁/2 +F_а∙ d₁ / 4 .

-на участке от опорыВ до точки зацепления (справа от сечения):

М_ИВ = R_Ву∙ z;где 0 ≤ z ≤ l₁

Приz = 0 М_ИВ =0; при z = l₁М_ИВ= F_r∙l₁/2 - F_а∙ d₁ / 4 .
2). Тихоходный вал

Внутренний крутящий момент на участке от опоры А до полюса зацепления равен нулю. В точке зацепления момент с шестерни передается на колесо, и далее на вал действует постоянный крутящий момент Т₂ до опоры В.

Определяем реакции в опорах:

Уравнения равновесия в горизонтальной плоскости

ΣM_B = R_AX∙2l- F_t∙l = 0; R_AX = F_t/2.

ΣX = -R_AX - R_BX + F_t= 0; R_BX = F_t - R_AX = F_t /2.

Уравнения равновесия в вертикальной плоскости

---

Смотрите также файлы

• Монтаж технологический оборудование фундаментный.rtf

• Новый фгос третьего поколения изменения стандартов.pdf

• I. резюме проекта.docx

• Фпсо б20ИОз.docx

• Образования белгородский государственный национальный.docx