ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N 303

1. В одном ящике 8 белых и 12 красных шаров, в другом ящике 10 белых, 5 черных и 5 красных шаров. Из первого переложили неизвестный шар во второй, а затем из второго достали два шара.

а) В какую теоретическую схему “укладывается" эта задача?

б) Записать соответствующую расчетную формулу и пояснить смысл входящих в нее величин.

в) Какие значения для данного условия принимают величины, входящие в указанную выше формулу?

г) Какова вероятность того, что оба шара черные.

Решение.

а) Если событие А может произойти только при выполнении одного из событий 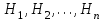, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле полной вероятности.

б) По условию из первого переложили неизвестный шар во второй, тогда возможны два случая: 1) переложили белый шар; 2) переложили красный шар. Применима формула полной вероятности .

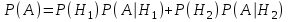Событие А = «Из второго ящика достали два черных шара» ( из г)).

Гипотезы: 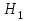= «Во второй ящик переложили из первого белый шар».

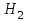= «Во второй ящик переложили из первого красный шар».

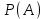- вероятность события А, 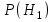, 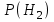- вероятности гипотез, 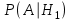, 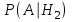- условные вероятности события А, при условии что имели место гипотезы , .

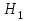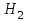в) Всего в первом ящике имеется 8+12=20 шаров, тогда вычислим вероятности гипотез , .

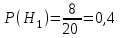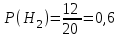Вычислим условные вероятности события А.

---

Если имела место гипотеза , то во втором ящике стало 10+1=11 белых, 5 черных и 5 красных шаров, всего 11+5+5=21, значит .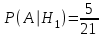

Если имела место гипотеза , то во втором ящике стало 10 белых, 5 черных и 5+1=6 красных шаров, всего 10+5+6=21, значит .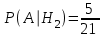

г) Вычислим .

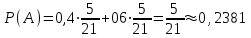Ответ: а) формула полной вероятности,

б) ,

в) , , , ,

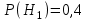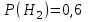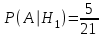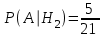г) .
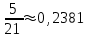2. Монета подбрасывается 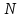раз, герб выпадает 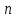раз.

а) В какую теоретическую схему “укладывается" эта задача?

б) Записать соответствующую расчетную формулу и пояснить смысл входящих в нее величин , .

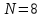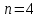в) Найти вероятность того, что при 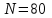герб выпадет 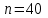раз; герб выпадет от 30 до 50 раз.

г) Какое число выпадений герба наиболее вероятно и почему?

Решение.

а) Имеем повторение испытаний. Вероятность появления события – появления герба в каждом эксперименте постоянна и равна 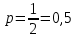. Тогда имеем схему Бернулли (это биномиальное распределение).

б) Формула Бернулли определяет вероятность появления ровно т раз события А в серии из 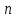  независимых испытаний, в каждом из которых вероятность появления события А равна р:

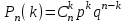, где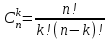

---

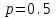, - вероятность появления герба, 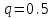- вероятность противоположного события.

По условию 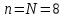, , 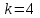тогда вычислим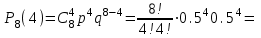



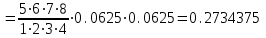
_{в) Найдем вероятность того, что при} герб выпадет раз.

Количество испытаний велико и применение формулы Бернулли в данном случае проблематично (сложно вычислить количество сочетаний 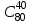и вероятности ).

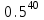Если вероятность 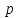  появления случайного события    в каждом испытании постоянна, то вероятность   того, что в   испытаниях событие   наступит ровно   раз, приближённо равна:
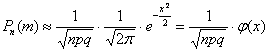 , где  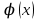, - функция Лапласа, ее значения табличны.

Найдем вероятность того, что при испытаний успех имели в 40 из них.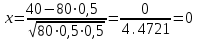

, ,

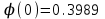Тогда .

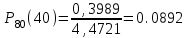Найдем вероятность того, что при герб выпадет от 30 до 50 раз.

Вероятность того, что в испытаниях событие наступит не менее 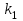и не более 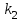раз находится по формуле: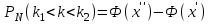

---

, где 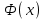- функция Лапласа, ее значения определяются с помощью таблицы.

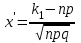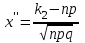, , тогда

, .

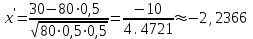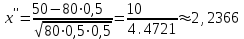Учитывая, что функция Лапласа нечетная получим:



.

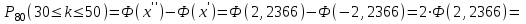
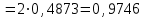г) Наиболее вероятное число успехов 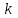при биномиальном распределении ( схема Бернулли) определяется из неравенства с учетом, что 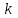-целое число.

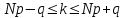, а поскольку 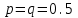находим

.

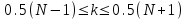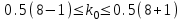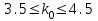Тогда для вычислим , , значит 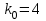, для вычислим 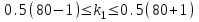, , 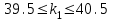значит .

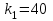Ответ: а) схема Бернулли,

б) ,

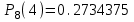в) , ,

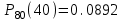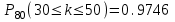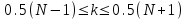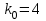г) для произвольного : , для - , для - .
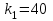3. СВ

---

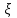
равномерно распределена на отрезке 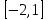. Найти плотность вероятности СВ 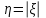. Построить график функции .

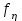Решение.

Запишем функцию плотности распределения для случайной величины , равномерна распределенной на отрезке : .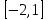

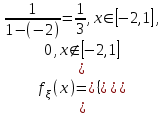Функция 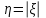не монотонна на отрезке .

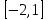При 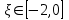имеем 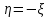она строго убывает, а при 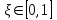находим 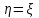- строго возрастает.
Применим формулу 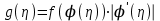, где 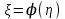- обратная функция к .

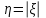При 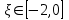находим, что 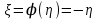, тогда 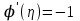, причем 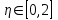, значит .

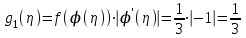При 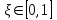находим что 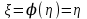, тогда 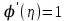, причем 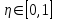, значит .

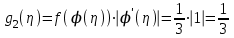По правилу 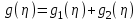определяем, что при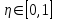 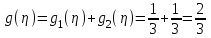, а при

---

Смотрите также файлы

• Моей сего презентации о создании компании икеи истории успеха и социальной значимости.odt

• Одонтогенная киратокиста .docx

• Группы крови. Их связь с характером человека.pptx

• Профессора рузуддинова.docx

• Что такое категория грунта Как она определяется Категория грунта это группа грунта, которая определяется по его составу.pptx