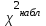, тем сильнее довод против основной гипотезы.

Поэтому критическая область для этой статистики всегда правосторонняя: [ ;+∞).

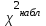Её границу 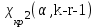находим по таблицам распределения 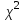и заданным значениям 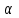, k = 7, r=2 (параметры и 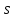оценены по выборке).

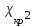(0.05;4) = 9,48773; 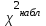= 6.98

Наблюдаемое значение статистики Пирсона не попадает в критическую область: 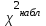< 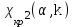, поэтому нет оснований отвергать основную гипотезу. Это позволяет утверждать, что опытные данные на заданном уровне значимости не противоречат гипотезе о нормальном законе распределения, или опытные данные согласуются с выдвинутой гипотезой.

Ответ: а) рис.1, математическое ожидание - выборочное среднее 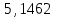, выборочная дисперсия 0,585.

б) опытные данные согласуются с выдвинутой гипотезой.

---

Смотрите также файлы

• Моей сего презентации о создании компании икеи истории успеха и социальной значимости.odt

• Одонтогенная киратокиста .docx

• Группы крови. Их связь с характером человека.pptx

• Профессора рузуддинова.docx

• Что такое категория грунта Как она определяется Категория грунта это группа грунта, которая определяется по его составу.pptx