Добавлен: 29.11.2023
Просмотров: 47
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
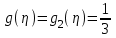 .
.Обобщая полученные данные, найдем что
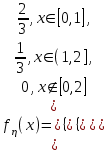
Построим график найденной функции.
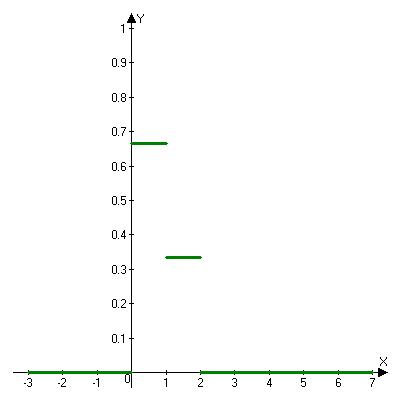
Рис.1.
Ответ:
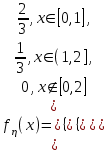 , рис.1.
, рис.1.4. Задана двумерная СВ
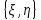 :
:Таблица 1.
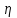 \ \ | -1 | 0 | 1 |
| -1 | 1/8 | 1/12 | 7/12 |
| 1 | 5/24 | 1/6 | 1/8 |
Найти а) безусловные законы распределения и центр,
б) условный закон распределения
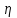 при
при 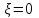 и, в) условное матожидание,
и, в) условное матожидание,г) распределение
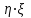
Решение.
Заданное распределение не является совместным законом распределения СВ
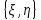 , поскольку сумма всех вероятностей равна
, поскольку сумма всех вероятностей равна 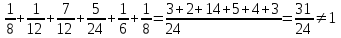 , заметим, что если вместо
, заметим, что если вместо 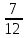 ( при
( при 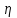 =-1 и
=-1 и  =1) положить
=1) положить 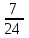 , то получим
, то получим 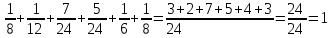 .
.Все дальнейшие расчеты будем производить для совместного распределения (иначе не получим ряды распределения)
Таблица 2.
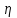 \ \ | -1 | 0 | 1 |
| -1 | 1/8 | 1/12 | 7/24 |
| 1 | 5/24 | 1/6 | 1/8 |
Для того, что бы найти безусловный закон распределения
 выполним сложение вероятностей по столбцам.
выполним сложение вероятностей по столбцам.Таблица3.
 | -1 | 0 | 1 |
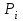 | 1/8+5/24=1/3 | 1/12+1/6=1/4 | 7/24+1/8=5/12 |
Для того, что бы найти безусловный распределения
 выполним сложение вероятностей по строкам.
выполним сложение вероятностей по строкам.Таблица 4.
 | -1 | 1 |
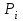 | 1/8+1/12+7/24=1/2 | 5/24+1/6+1/6=1/2 |
Вычислим математические ожидания
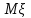 и
и 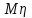 .
.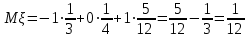 ,
,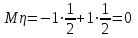 .
.Центр распределения:
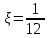 ,
, 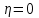 .
.Б) найдем условный закон распределения
 при
при  .
.В таблице 3 найдено
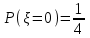 .
.Условный закон распределения случайной величины
 , найдем применяя формулу
, найдем применяя формулу 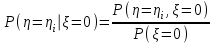 тогда
тогда 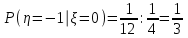 ,
, 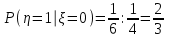
То есть
Таблица 5.
 / / | -1 | 1 |
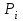 | 1/3 | 2/3 |
в) Найдем условное математическое ожидание
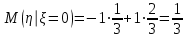 .
.г) Найдем закон распределения СВ распределение
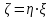 .
.Вычислим все возможные произведения и запишем их вероятности
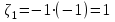 ,
, 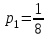 ,
, 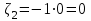 ,
, 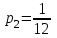 ,
, 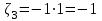 ,
, 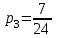 ,
,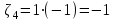 ,
, 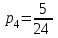 ,
, 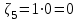 ,
, 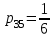 ,
,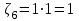 ,
, 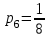 .
.Объединим одинаковые значения и вычислим
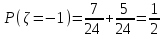 ,
, 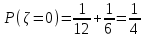 ,
, 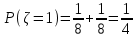 .
. Таблица 6.
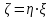 | -1 | 0 | 1 |
 | 1/2 | 1/4 | 1/4 |
Ответ: заданное распределение не является законом распределения, рассматриваем распределение из таблицы 2.
а) таблица3, таблица 4, центр
 ,
,  .
.б) таблица 5, в)
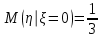 , г) таблица 6.
, г) таблица 6.5. Распределение СВ в выборке определяется следующим интервальным рядом распределения.
Таблица 7.
| 3,0-3,6 | 3,6-4,2 | 4,2-4,8 | 4,8-5,4 | 5,4-6,0 | 6,0-6,6 | 6,6-7,2 |
| 2 | 8 | 35 | 43 | 22 | 15 | 5 |
а) построить гистограмму и найти оценки мат ожидания и дисперсии.
б) Как проверить гипотезу о нормальном законе распределения при уровне значимости
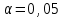 .
.Решение.
а) Построим гистограмму частот заданного ряда распределения, отметив на оси абсцисс – интервалы распределения, а на оси ординат их частоты и построим прямоугольники.
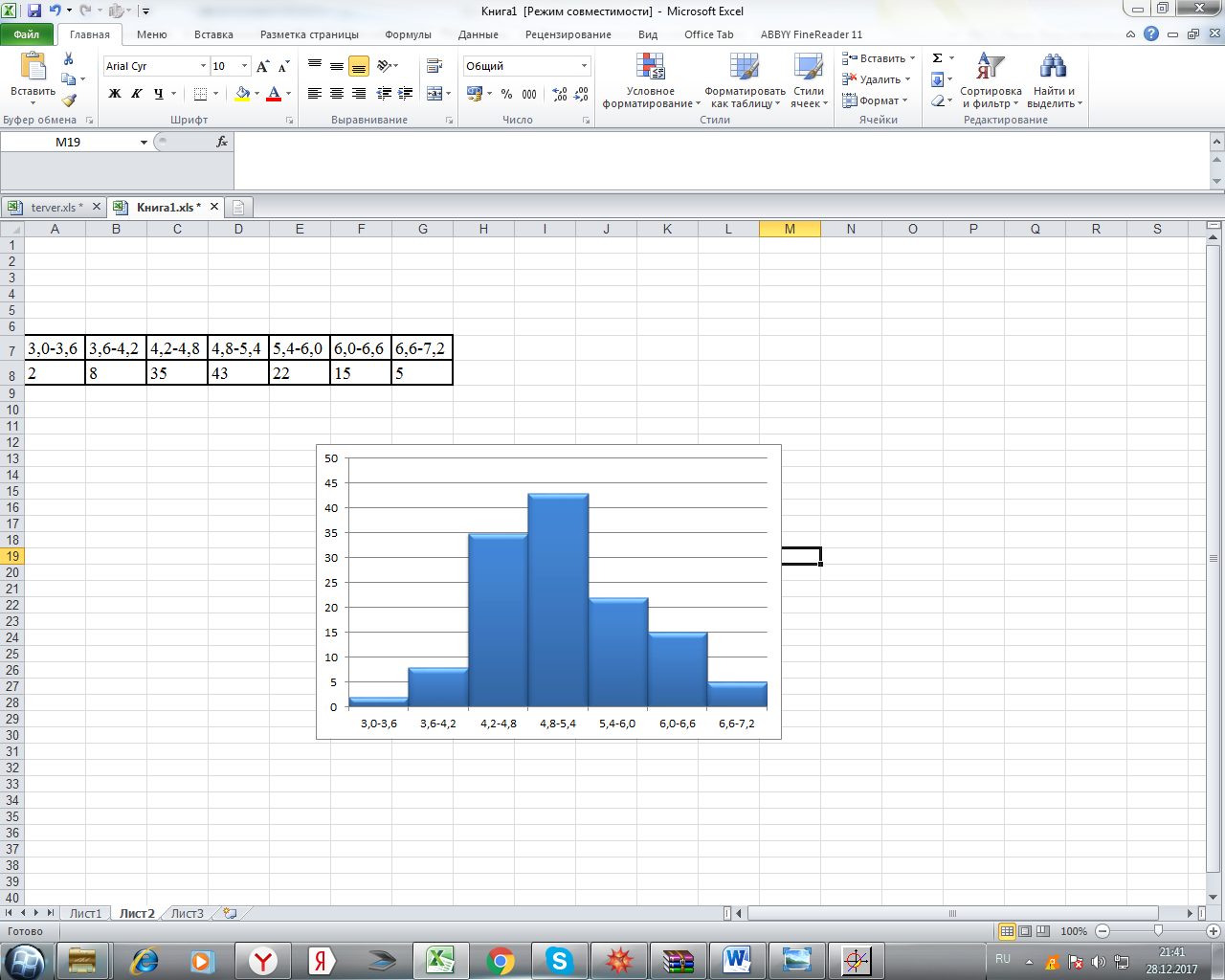
Рис.1. Полигон частот.
Что бы найти оценки мат ожидания и дисперсии перейдем к вариационному ряду, взяв в качестве вариант середины интервалов.
Таблица 8.
| Х | 3.3 | 3.9 | 4.5 | 5.1 | 5.7 | 6.3 | 6.9 |
| N | 2 | 8 | 35 | 43 | 22 | 15 | 5 |
Объем выборки
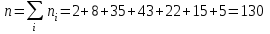 .
.Выборочное среднее
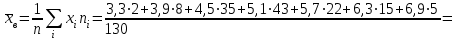
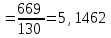 .
.Выборочная дисперсия
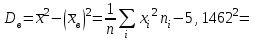
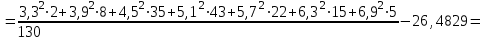
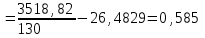
б) Критерием согласия называется критерий поверки гипотезы о предполагаемом законе распределения. В соответствии с критерием Пирсона сначала вычисляется величина
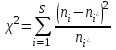 ,
, где
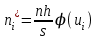 - теоретические частоты,
- теоретические частоты, 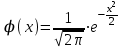 – функция Лапласа, значения которой табулированы и приводятся в таблицах.
– функция Лапласа, значения которой табулированы и приводятся в таблицах. Вычислим теоретические частоты, учитывая, что:
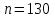 ,
, 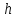 =0,6 (ширина интервала),
=0,6 (ширина интервала), 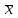
= 5,1462,
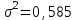 ,
, 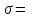 0,7648.
0,7648.Сравним эмпирические и теоретические частоты.
Таблица 9.
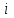 | 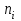 | 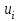 | 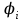 | 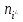 | 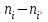 | 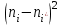 | 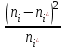 |
| 1 | 2 | -2.4138 | 0,0213 | 2.172 | 0.1723 | 0.02968 | 0.0137 |
| 2 | 8 | -1.6293 | 0,1057 | 10.78 | 2.7798 | 7.7274 | 0.717 |
| 3 | 35 | -0.8448 | 0,278 | 28.352 | -6.6482 | 44.198 | 1.559 |
| 4 | 43 | -0.06035 | 0,398 | 40.59 | -2.41 | 5.8079 | 0.143 |
| 5 | 22 | 0.7242 | 0,3056 | 31.167 | 9.1666 | 84.027 | 2.696 |
| 6 | 15 | 1.5087 | 0,1276 | 13.013 | -1.9867 | 3.947 | 0.303 |
| 7 | 5 | 2.2932 | 0,0283 | 2.886 | -2.1138 | 4.4682 | 1.548 |
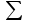 | 130 | | | 130 | | | 6,98 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение