Осуществите следующие действия:

- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;

- определите эффект замены (по Хиксу);

- определите эффект дохода (по Хиксу);

- определите общий эффект (по Хиксу);

- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Решение

1. Бюджетное ограничение по заданным значениям m = 240 ден. ед., p_x = 4 ден. ед. и p_y = 8 ден. ед. принимает вид: 4x + 8y 240 => y = 30 – 0,5x – уравнение бюджетной линии.
Условие равновесие потребителя:
.
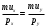mu_x = (u)_x’ = (xy²)_x’ = y²;

mu_y = (u)_y’ = (xy²)_y’ = 2xy;

;

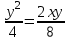8y² = 8xy;

y = x;
y = 30 – 0,5 * y;

y + 0,5y = 30;

1,5y = 30 => y = 20 => x = 20.
Проверка:


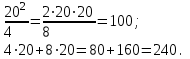
Уравнение кривой безразличия:

u(x) = 20 * 20² = 8000;

8000 = xy² => y = .
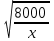Оптимальный выбор потребителя графически представлен на рисунке 3.1.

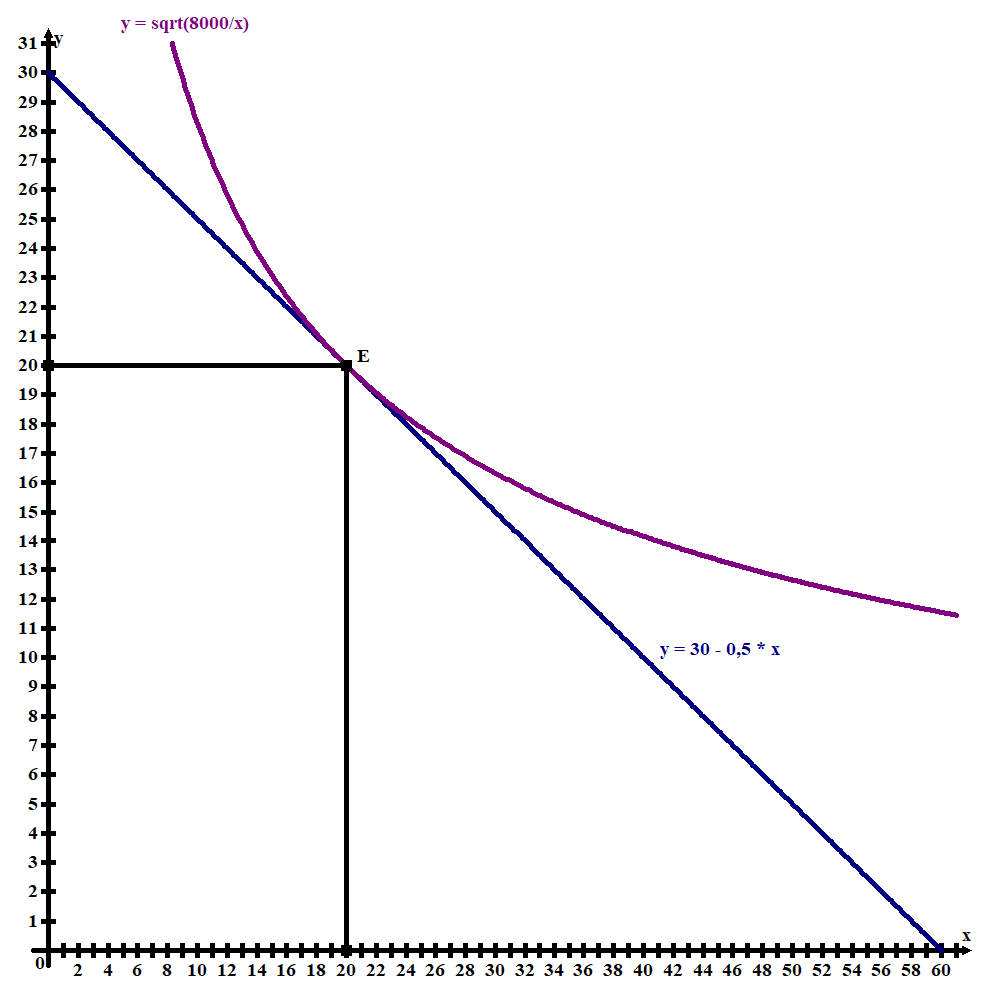
Рисунок 3.1 – Потребительский выбор
Исходя из рисунка 3.1, первоначальный потребительский набор (x,y) = (20; 20).
Изменение цены блага влияет на объём покупательского спроса через действие эффекта дохода и эффекта замещения (замены). При понижении цены какого-либо блага потребитель перемещается на более высокую кривую безразличия. Это повышение полезности является следствием увеличения реальной покупательной способности. Увеличение реальной покупательной способности – это результат комбинации двух составляющих: изменения реального дохода и изменения относительных цен. Это означает, что:

1) во-первых, при падении цены реальный доход потребителя, то есть количество товаров, которое потребитель может купить, растёт (потребитель ощущает себя богаче) (эффект дохода);

2) во-вторых, в случае понижения цены данный товар становится для потребителя относительно более дешёвым по сравнению с товаром, цена которого не изменилась (эффект замены).

Как правило, эти два процесса происходят одновременно.

Таким образом, рациональный потребитель заменит часть относительно более дорогого товара более дешёвым, то есть увеличит потребление подешевевшего товара.

---

2. Метод Хикса заключается в том, что разные уровни денежного дохода позволяют достичь одной и той же кривой безразличия и представляют собой одинаковый уровень дохода. Эффект замещения интерпретируется как изменение в величине спроса, вызванное движением относительной цены блага при постоянном уровне полезности реального дохода потребителя.

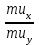
Исходя из условия оптимального выбора, угол наклона кривой безразличия 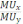равен углу наклона бюджетного ограничения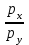 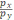. Решаем систему уравнений аналогично:

4x + 5y = 240 => y = 48 – 0,8x – уравнение новой бюджетной линии;

;

mu_x = (u)_x’ = (xy²)_x’ = y²;

mu_y = (u)_y’ = (xy²)_y’ = 2xy;

;

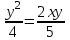5y² = 8xy;

y = 1,6x;
1,6x = 48 – 0,8x;

2,4x = 48;

x = 20 => y = 32.
Проверка:


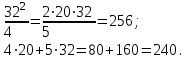
Уравнение новой кривой безразличия:

u(x) = 20 * 32² = 20480;

20480 = xy² => y = .
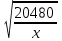В результате конечный потребительский набор (x,y) = (20; 32).
График потребительского выбора представлен на рисунке 3.2.

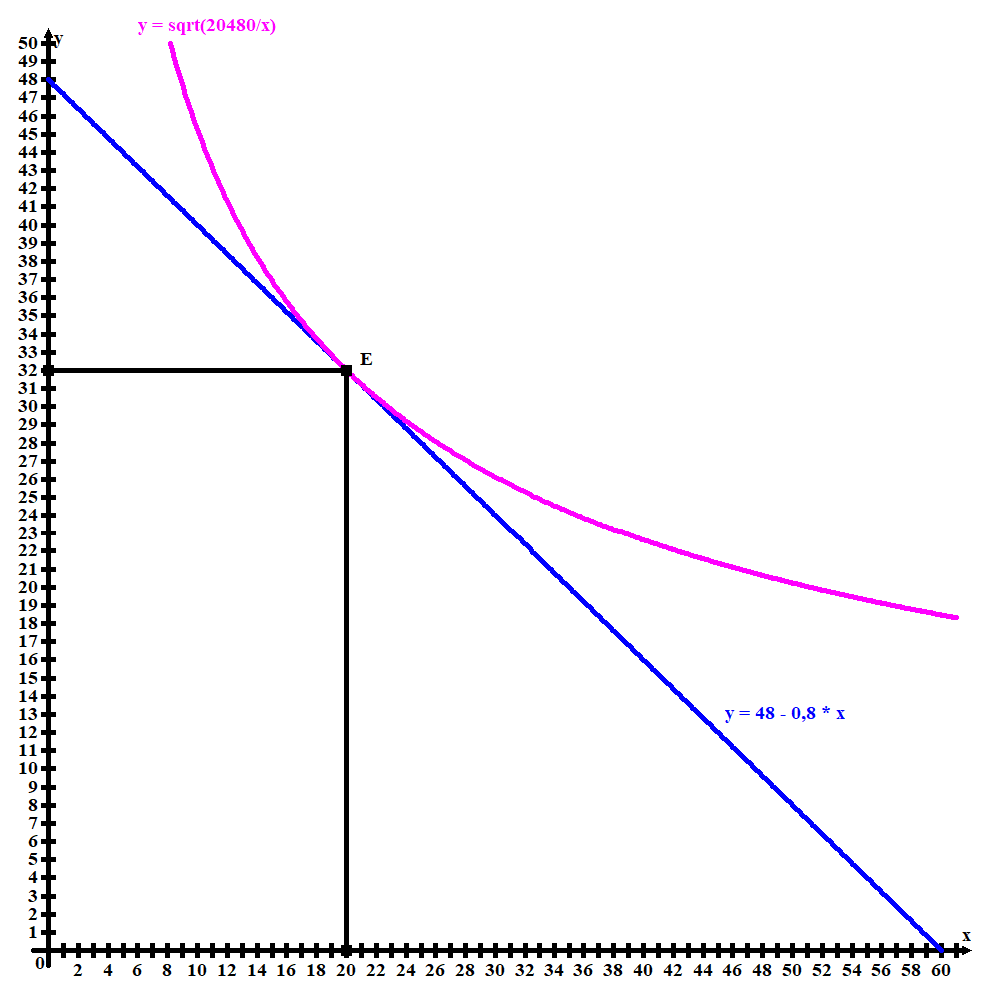
Рисунок 3.2 – Новый потребительский выбор
Общий эффект показывает изменение объёма потребления товара при изменении его цены. Если зависимость между изменением цены и объёмом потребления данного товара прямая, то есть закон спроса нарушен, то такие блага называют товарами Гиффена.

В случае понижения цены на второй товар он становится для потребителя относительно более дешёвым по сравнению с первым товаром, ведь его цена не изменилась. Рациональный потребитель заменит часть относительно более дорогого товара (y) относительно более дешёвым (x), то есть увеличит потребление подешевевшего товара.
Общий эффект = 32 – 20 = 12.
3. Эффект замены (по Хиксу) показывает, на сколько бы изменился объём потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.

---

Необходимо построить вспомогательное бюджетное ограничение. Это параллельная прямая к первоначальной кривой бюджетного ограничения (до точки касания с первоначальной кривой безразличия). Получится новая кривая бюджетного ограничения.
4 * 20 + 5 * 20 = 80 + 100 = 180 < 240;

4x + 5y = 180 => y = 36 – 0,8x;

36 – 0,8x = ;

(36 – 0,8x)² = ( )²;

1296x – 57,6x 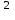+ 0,64x³ – 8000 = 0;

x = 20 => y = 36 – 0,8 * 20 = 36 – 16 = 20.
Промежуточный потребительский набор (x,y) = (20; 20).
График потребительского выбора представлен на рисунке 3.3.

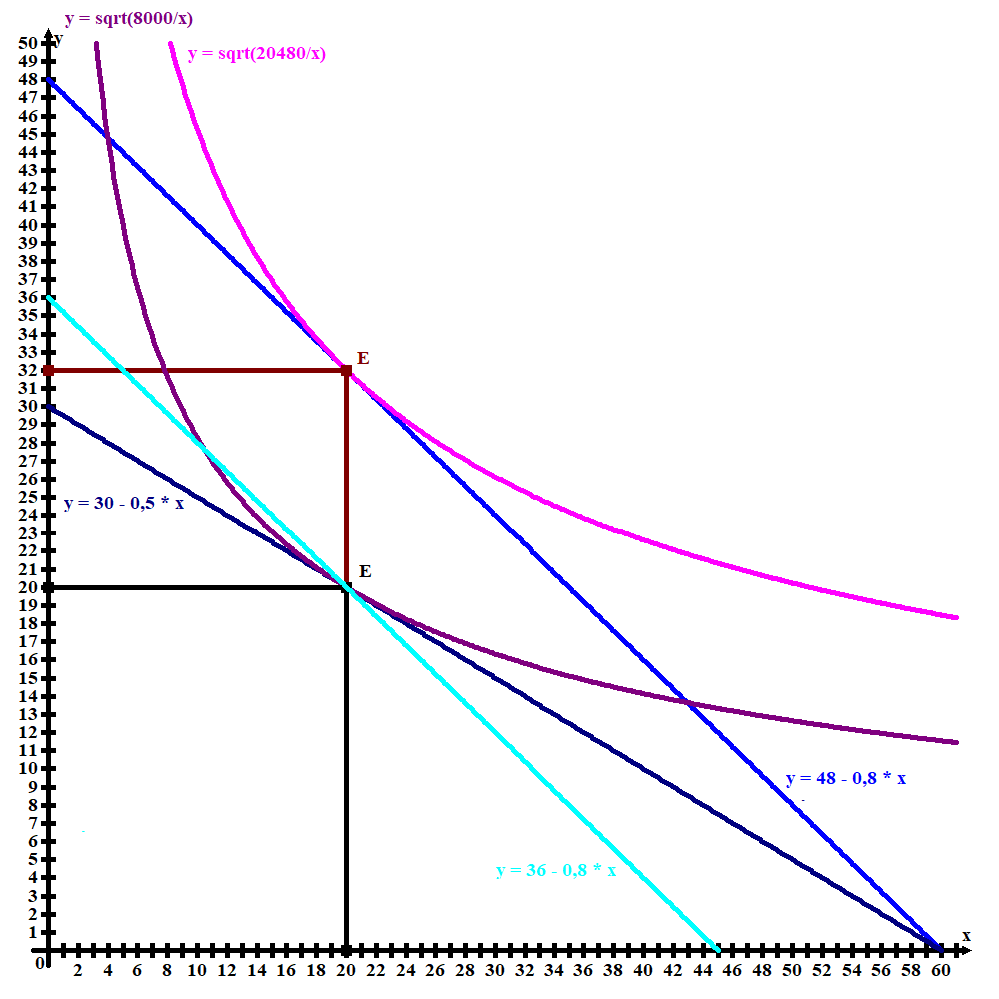
Рисунок 3.3 – График потребительского выбора
Исходя из рисунка 3.3, эффект замены при понижении цены товара y с 8 ден. ед. до 5 ден. ед.:

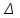y = 20 – 20 = 0.
4. Эффект дохода (по Хиксу) показывает, на сколько изменится объём данного блага за счёт того, что потребитель начинает чувствовать себя богаче (повышение реального дохода потребителя при понижении цены на товар):

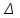y = 32 – 20 = 12.
Общий эффект = эффект замены + эффект дохода = 0 + 12 = 12.
Вывод: зависимость между изменением цены (5 < 8) и объёмом потребления данного товара y (32 > 20) обратная, то есть закон спроса не нарушен, то данный товар – нормальный.
Практическое задание 4

Поведение производителя и конкуренция

Задача 1

Технологическая норма замещения факторов L и K равна MRS = -0,5. Предположим, что фирма готова произвести тот же самый объём выпуска, но сократить использование фактора K на 2 единицы. Сколько дополнительных единиц фактора L потребуется фирме?
Решение

Условие оптимального использования ресурсов:
MRS_KL = - 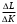при Q = const,
где MRS_KL – технологическая норма замещения фактора L фактором K.
Предположим, что фирма готова произвести тот же самый объём выпуска, но сократить использование фактора K на 2 единицы:

-0,5 = =>

---

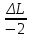L = +1 единица.
Таким образом, в результате проведенных расчётов, фирме потребуется дополнительных единиц фактора L в размере 1 единицы.
Графическое решение представлено на рисунке 4.1.

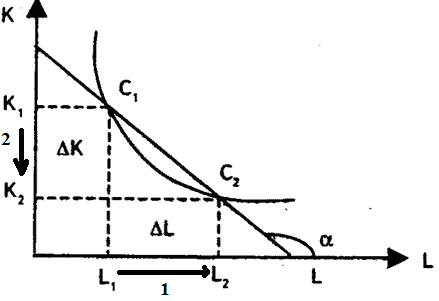
Рисунок 4.1 – Графическое решение задачи (схематично)
Практическое задание 5

Рыночные структуры и стратегия поведения

Задача

Предположим, что на рынке действуют две фирмы, функции общих издержек TC заданы уравнениями: TC₁(q₁) = 20 + q₁² и TC₂(q₂) = 20 + 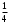q₂². Рыночный спрос описывается функцией:
P(Q) = 1000 – 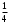Q,
где Q = q₁ + q₂.
Определите объём продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.
Решение

1. Стратегия по Курно предполагает, что:

1) две фирмы производят однородный товар;

2) фирмам известна кривая рыночного спроса;

3) фирмы принимают решения о производстве независимо друг от друга и одновременно;

4) каждая из фирм предполагает выпуск конкурента постоянным.
Решение задачи по Курно.

Отраслевой спрос представлен линейной функцией:
P = a – bQ,
где a, b – положительные константы;

Q – объём рыночного спроса, складывается из объёмов предложения первой (q₁) и второй (q₂) фирм (Q = q₁ + q₂) при цене P.
P(Q) = 1000 – 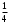Q => a = 1000, b = 0,25.

Тогда линейный спрос можно представить как:

P = a – b * (q₁ + q₂) = a – bq₁ – bq₂;

P = 1000 – 0,25 * (q₁ + q₂) = 1000 – 0,25q₁ – 0,25q₂.

Обе фирмы такие условия по издержкам производства:
TC = FC + VC,
где FC – постоянные издержки (не зависят от объёма продаж и существуют даже при отсутствии производства);

VC – переменные издержки.
TC₁(q₁) = 20 + q₁²;

TC₂(q₂) = 20 + 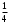q₂².

Прибыли олигополистов можно выразить так:

П₁ = TR₁ – TC

---

₁ = P * q₁ – TC₁;

П₂ = TR₂ – TC₂ = P * q₂ – TC₂;

П₁ = (1000 – 0,25q₁ – 0,25q₂) * q₁ – (20 + q₁²);

П₁ = 1000q₁ – 0,25q₁² – 0,25q₁q₂ – 20 – q₁²;

П₁ = 1000q₁ – 1,25q₁² – 0,25q₁q₂ – 20;

П₂ = (1000 – 0,25q₁ – 0,25q₂) * q₂ – (20 + q₂²);

П₂ = 1000q₂ – 0,25q₁q₂ – 0,25q₂² – 20 – 0,25q₂²;

П₂ = 1000q₂ – 0,25q₁q₂ – 0,5q₂² – 20.

Условие максимизации прибыли предполагает невозможность прироста прибыли в оптимальной точке, или другими словами равенство производной от прибыли нулю:

П₁’ = ;

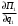(1000q₁ – 1,25q₁² – 0,25q₁q₂ – 20)_q1’ = 0;

1000 – 2,5q₁ – 0,25q₂ = 0;

1000 – 0,25q₂ = 2,5q₁;

q₁ = 400 – 0,1q₂ – уравнение реакции фирмы 1 => q₂ = 4000 – 10q₁ (для построения графика);

П₂’ = 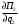= 0;

(1000q₂ – 0,25q₁q₂ – 0,5q₂² – 20)_q2’ = 0;

1000 – 0,25q₁ – q₂ = 0;

q₂ = 1000 – 0,25q₁ – уравнение реакции фирмы 2.

Воспользуемся программой MathCad для решения системы уравнений из кривых реакции:















q₁ = 363,64 ед.; q₂ = 909,09 ед. – объём продаж, который будет у каждой фирмы;

P = 1000 – 0,25 * (363,64 + 909,09) = 681,82 ден. ед. – цена, которая установится на рынке, если фирмы конкурируют по Курно.
Графическое решение представлено на рисунке 5.1.

---

Смотрите также файлы

• 08. 12. 2021 г., Гу мвд россии по г.rtf

• Контрольная работа Курсовая работа Тема уже дана Самостоятельный выбор темы Небольшой объём работы Большой объем работы.docx

• Занятость учащихся 8 В класса во внеурочное время 2022 2023 учебный год (с учетом регулярных и нерегулярных занятий).docx

• Конспект занятия Путешествие в мир химии.doc

• Финансы предприятий и организаций.docx