ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 227
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 5.1 – Графическое решение задачи (модель Курно)
2. Стратегия по Бертрану предполагает, что в отличие от моделей Курно и Штакельберга предполагают наличие ценового взаимодействия фирм на олигополистическом рынке. Таким образом, конкуренция заключается в том, что каждая фирма устанавливает свою цену:
1) на рынке действуют две фирмы;
2) продукт производится однородный;
3) целью каждой фирмы является максимизация прибыли;
4) отсутствуют соглашения фирм друг с другом;
5) фирмы назначают цены одновременно так, что каждая не может прогнозировать реакцию конкурента на сделанный ею самой выбор.
В соответствии с данным условием решение задачи по Бертрану принимает вид (рыночный спрос описывается функцией):
Q =
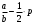 .
.P(Q) = 1000 –
 Q => a = 1000, b = 0,25.
Q => a = 1000, b = 0,25.Две фирмы выбирают цены p1 и p2. Затраты фирм носят пропорциональный характер:
TC1(q1) = 20 + q12 и TC2(q2) = 20 +
 q22.
q22.Стратегическое поведение фирм в данной модели можно назвать войной цен.
Ценовая война – это цикл последовательных уменьшений цены соперничающими на олигополистическом рынке фирмами.
Снижая цену ниже цены своего конкурента, каждый продавец стремиться захватить весь рынок. Но конкурент также отвечает понижением цены.
Война цен продолжается до тех пор, пока цена не падает до уровня предельных и средних издержек – до конкурентного равновесия: p* = МС = АС = с.
В условиях равновесия фирмы получают нулевую экономическую прибыль и делят рынок поровну, поскольку товар они продают по одинаковой цене.
Спрос на продукцию одного дуополиста формируется в зависимости от соотношения цен обоих дуополистов.
По аналогии:
П1’ =
 ; p1 = 1000 – 0,25q1;
; p1 = 1000 – 0,25q1;П1 = (1000 – 0,25q1) * q1 – (20 + q12) = 1000q1 – 0,25q12 – 20 – q12;
П1 = 1000q1 – 1,25q12 – 20;
П1’ = (1000q1 – 1,25q12 – 20)’ = 1000 – 2,5q1 = 0;
1000 = 2,5q1 => q1 = 400 => p1 = 1000 – 0,25 * 400 = 900;
П2’ =
 = 0; p2 = 1000 – 0,25q2;
= 0; p2 = 1000 – 0,25q2;П2 = (1000 – 0,25q2) * q2 – (20 + 0,25q2
2);
П2 = 1000q2 – 0,25q22 – 20 – 0,25q22;
П2 = 1000q2 – 0,5q22 – 20;
П2’ = (1000q2 – 0,5q22 – 20)’ = 0;
1000 – q2 = 0 => q2 = 1000 => p2 = 1000 – 0,25 * 1000 = 750.
При p1 = 900 > p2 = 750 спрос нулевой, так как все покупатели предпочтут более низкую цену второго дуополиста – вертикальный отрезок кривой спроса.
Графическое решение представлено на рисунке 5.2.
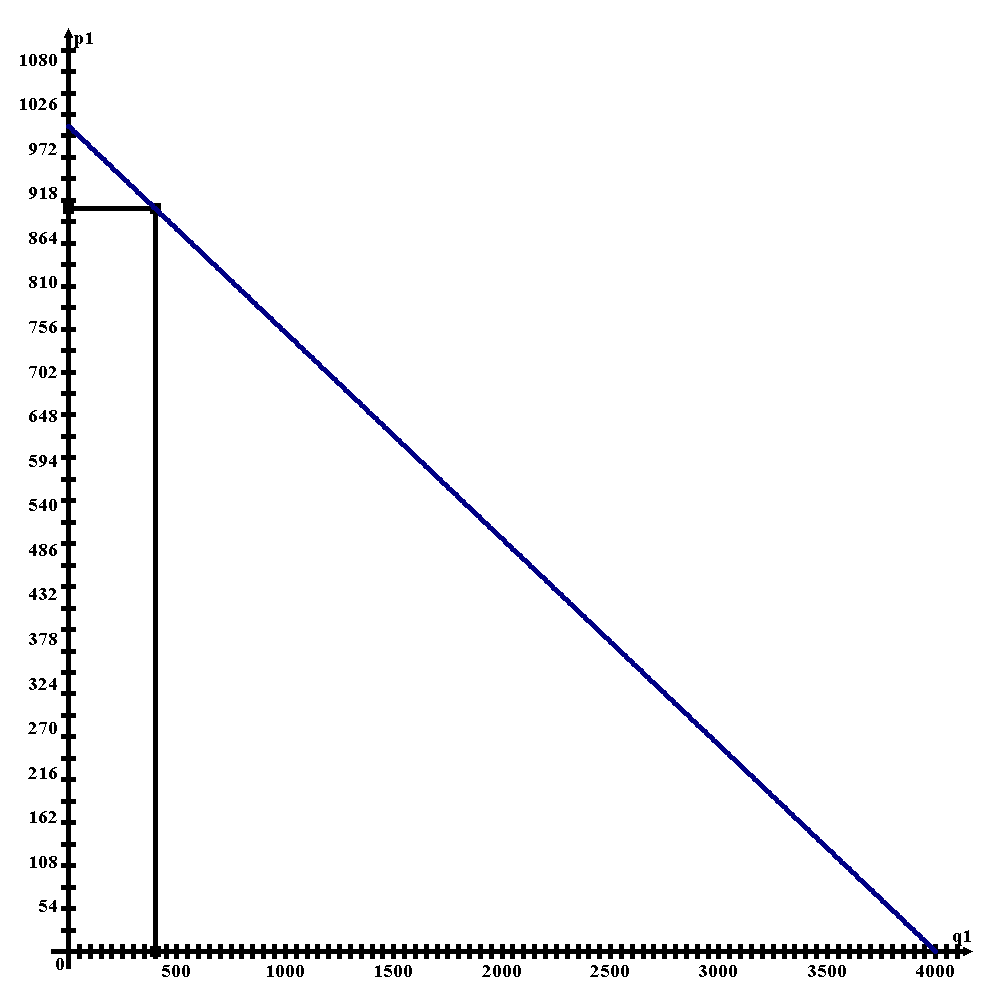
Рисунок 5.2 – Графическое решение задачи (модель Бертрана)
3. Стратегия по Штакельбергу предполагает, что она рассматривает проблему ассиметричной конкуренции дуополистов, осуществляющих стратегическое взаимодействие по принципу «лидер – последователь». Олигополисты выбирают две линии поведения: лидера и последователя. Последователь будет реагировать на действия лидера, лидер придерживается противоположной точки зрения.
Решение задачи по сценарию Штакельберга принимает следующий вид.
Предполагаемая вариация лидера
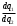 = 0, где q1 = f(q2) и является по сути первым уравнением реакции в модели Курно (q1 = 400 – 0,1q2), а предполагаемая вариация последователя
= 0, где q1 = f(q2) и является по сути первым уравнением реакции в модели Курно (q1 = 400 – 0,1q2), а предполагаемая вариация последователя 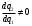 , где q2 = f(q1) является вторым уравнением реакции в модели Курно (q2 = 1000 – 0,25q1). Разница в том, что выпуск лидера в 2 раза превышает выпуск последователя: q2 = 2q1:
, где q2 = f(q1) является вторым уравнением реакции в модели Курно (q2 = 1000 – 0,25q1). Разница в том, что выпуск лидера в 2 раза превышает выпуск последователя: q2 = 2q1:q1 = 400 – 0,1 * 2q1;
q1 = 400 – 0,2q1;
1,2q1 = 400 => q1 = 333,33;
q1 = 0,5q2;
q2 = 1000 – 0,25 * 0,5q2;
q2 = 1000 – 0,125q2;
1,125q2 = 1000 => q2 = 888,89;
P = 1000 – 0,25 * (333,33 + 888,89) = 694,45.
Графическое решение представлено на рисунке 5.3.
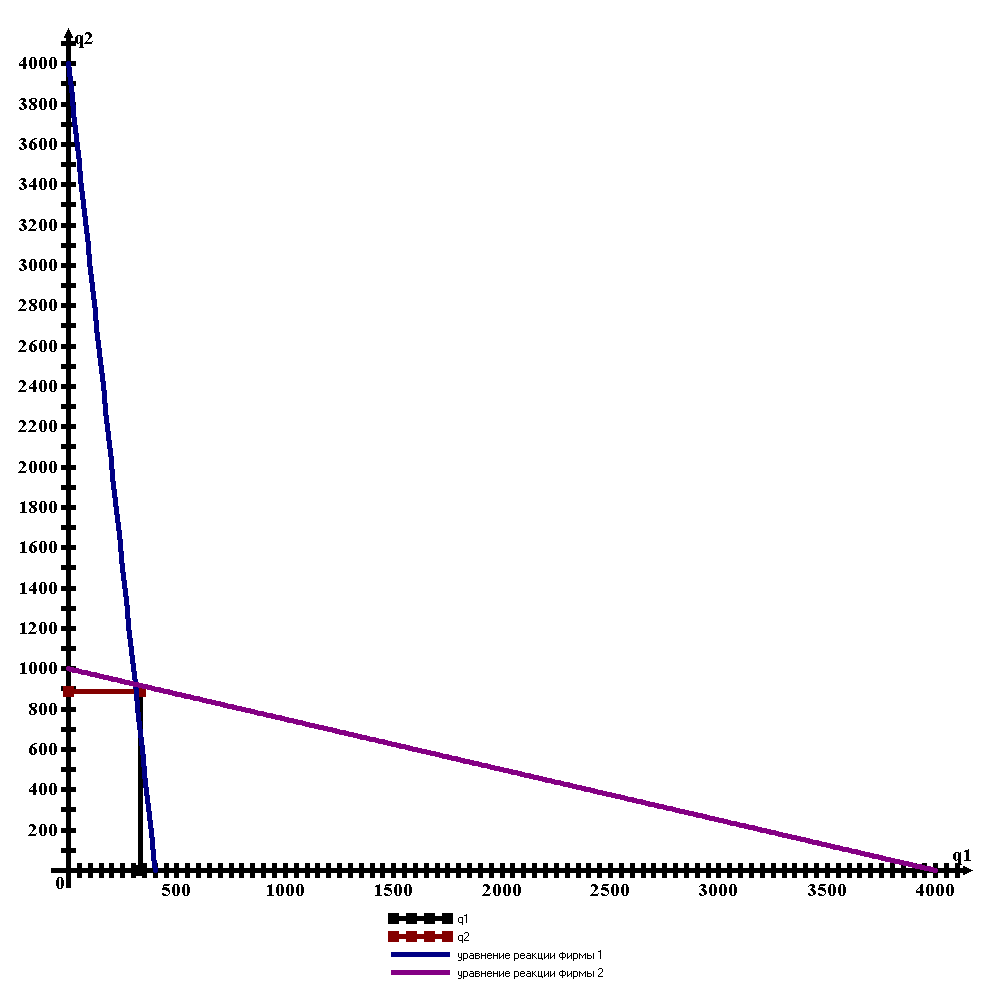
Рисунок 5.3 – Графическое решение задачи (модель Штакельберга)
Таким образом, сравнение объёмов производства и цен в модели Курно, модели Бертрана и модели Штакельберга:
| Модель | Объёмы производства | Цены P = a – bQ |
| Курно | q1* = 363,64; q2* = 909,09 | P* = 681,82 |
| Q* = q1* + q2* = 1272,73 | ||
| Штакельберга | q1* = 333,33; q2* = 888,89 | P* = 694,45 |
| Q = q1 + q2 = 1222,22 | ||
| Бертрана | q1 (p1, p2) = 400; q2 (p1, p2) = 1000 | p1 = 900; p2 = 750 |
Задача 2
График предельных издержек фирмы-монополиста задан условием MC = 2Q. Функция предельного дохода принимает вид: MR = 60 – 2Q. Определите эластичность рыночного спроса
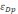
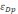 при оптимальном выпуске фирмы-монополиста.
при оптимальном выпуске фирмы-монополиста.Решение
1. Определяем оптимальный выпуск фирмы-монополиста:
MR = MC,
где MR – предельный доход;
MC – предельные издержки.
60 – 2Q = 2Q;
Q = 15 ед. – оптимальный выпуск фирмы-монополиста.
2. Выводим функцию спроса фирмы-монополиста:
MR = (TR)’ = (P * Q)’,
где TR – общий доход;
P – цена;
Q – выпуск.
MR = 60 – 2Q => TR = 60Q – Q2;
P * Q = 60Q – Q2;
P = 60 – Q – функция спроса фирмы-монополиста.
3. Цена при оптимальном выпуске фирмы-монополиста составит P = 60 – 15 = 45 ден. ед.
4. Эластичность
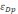
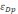 в точке, где:
в точке, где: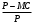 = -
= -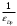 .
.МС = 2 * 15 = 30 ед.;
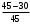 = -
= -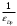 ;
;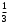 = -
= -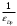 ;
;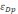 = |-3| > 1 – эластичность рыночного спроса при оптимальном выпуске фирмы-монополиста.
= |-3| > 1 – эластичность рыночного спроса при оптимальном выпуске фирмы-монополиста.Практическое задание 6
Общее равновесие и экономическая эффективность
Задача
Предположим, что издержки по вывозу мусора с территории двух районов составляют TC(x) = x2, где x – площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности u1(x, m1) = 8
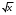 + m1, а предпочтения всех жителей 2-го района – u2(x, m2) = 4
+ m1, а предпочтения всех жителей 2-го района – u2(x, m2) = 4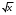 + m2, где m1 и m2 – потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.
+ m2, где m1 и m2 – потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.
Решение
1. Для определения Парето-эффективного значения вывоза мусора принимается условие, что оптимальное количество площади определяется точкой пересечения линий предельных затрат и предельной общей полезности:
MR = MC.
MRi = (TRi)’ = (Pi * mi);
MC = (TC)’ = (x2)’ = 2x;
TC = x2
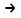 min.
min.Предпочтения – это по сути спрос:
P1 = 8
 + m1 => TR1 = (8
+ m1 => TR1 = (8 + m1) * m1 = 8
+ m1) * m1 = 8 m1 + m12;
m1 + m12;MR1 = (8
 m1 + m12)x’ =
m1 + m12)x’ = 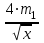 ;
;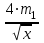 = 2x => 2
= 2x => 2 x = 4m1;
x = 4m1;P2 = 4
 + m2 => TR = (4
+ m2 => TR = (4 + m2) * m2 = 4
+ m2) * m2 = 4 m2 + m22;
m2 + m22;MR2 = (4
 m2 + m22)x’ =
m2 + m22)x’ = 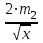 ;
;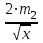 = 2x => 2
= 2x => 2 x = 2m2.
x = 2m2.2. Условие оптимального потребления:
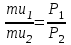 .
.mu1 = (8
 + m1)m1’ = 1;
+ m1)m1’ = 1;mu2 = (4
 + m2)m2’ = 1;
+ m2)m2’ = 1;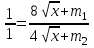 .
.Необходимо решить систему уравнений:
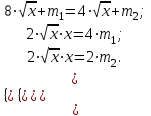
Решение: m1 = 8
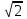 ; m2 = 16
; m2 = 16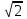 ; x = 8.
; x = 8.Парето-эффективное значение вывоза мусора: m1 = 11,31; m2 = 22,63.
Проверка:
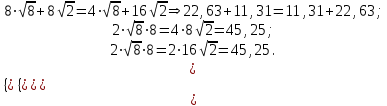
2. В результате решения:
u1 = 8 *
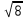 + m1 = 22,63 + m1;
+ m1 = 22,63 + m1;u2 = 4 *
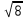 + m2 = 11,31 + m2.
+ m2 = 11,31 + m2.3. На рисунке 6.1 представлен график.
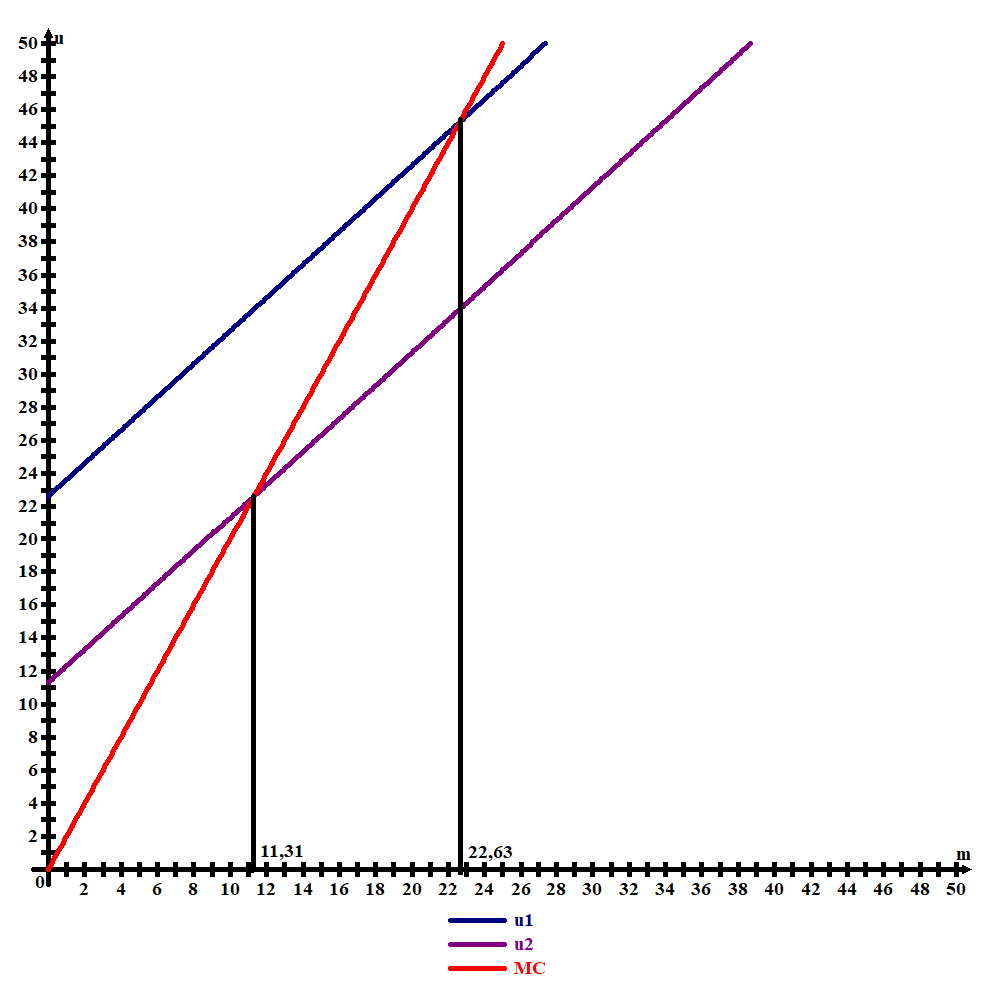
Рисунок 6.1 – Графическое решение задачи