Файл: Задача безмоментная теория и краевой эффект в составной оболочке.docx
Добавлен: 29.11.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.














 Задача: безмоментная теория и краевой эффект в составной оболочке
Задача: безмоментная теория и краевой эффект в составной оболочке
 Rв Rв
Rв Rв R
R 



 p
p

H1
H
x


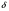
Исходные данные:
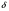 =2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув),
=2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув), 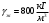 удельный вес жидкости.
удельный вес жидкости.Определить: усилия и перемещения в верхнем полусферическом днище и части цилиндрической обечайки от наддува по безмоментной теории, усилия и перемещения нижнего полусферического днища и части цилиндрической обечайки от наддува и гидростатического давления по безмоментной теории, решить задачу краевого эффекта в зоне стыка верхнего днища и цилиндрической обечайки.
Определение внутренних усилий в оболочке
-
Верхнее полусферическое днище воспринимает только наддув.
Меридиональное и окружное усилия определяются из двух уравнений равновесия – уравнения Лапласа (сумма проекций сил на нормаль к оболочке) и уравнения проекций сил на вертикальную ось:
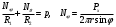 Здесь R1 и R2 – главные радиусы кривизны оболочки, r – радиус параллельного круга, Px – проекция равнодействующей внешней нагрузки на ось x, p – давление наддува.
Здесь R1 и R2 – главные радиусы кривизны оболочки, r – радиус параллельного круга, Px – проекция равнодействующей внешней нагрузки на ось x, p – давление наддува.-
Верхняя часть цилиндрической обечайки также воспринимает только наддув. Меридиональное и окружное усилия определяются по приведённым в пункте 1 формулам. -
Нижняя часть цилиндрической обечайки воспринимает наддув и гидростатическое давление. Суммарное давление на оболочку определяется формулой
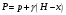 ,
, 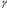 - удельный вес жидкости.
- удельный вес жидкости.Внутренние усилия определяются по приведённым в пункте 1 формулам.
-
Нижнее полусферическое днище воспринимает наддув и гидростатическое давление. Суммарное давление определить самостоятельно. Внутренние усилия определяются по тем же формулам.
Пояснение к уравнению проекций сил на вертикальную ось оболочки
Рисунок 1

 Px dp
Px dp
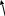
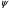 ds
ds 


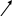
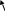

 pd
pd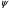

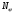 r
r  R
R 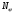
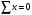
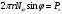 , отсюда
, отсюда 
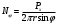
Определение Px
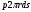 – элементарная сила, действующая на круговой элемент оболочки
– элементарная сила, действующая на круговой элемент оболочки 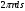 . Её проекция на ось x
. Её проекция на ось x 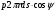 .
. 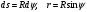

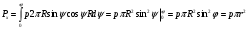
Тогда
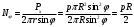
Полученная формула справедлива при p=const, если есть ещё гидростатическое давление (рис.3), переменное по высоте оболочки, то суммарное давление на стенки мы не можем вынести за знак интеграла. Необходимо интегрировать всё подынтегральное выражение.




 Рисунок 2 Px
Рисунок 2 Px


 Rв Rв
Rв Rв
 pR
pR
Nx Nx
Для цилиндрической оболочки меридиональное усилие обозначим Nx. Рисунок помогает составить уравнение проекций сил на вертикальную ось и найти Nx.
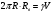 , где V – объём, занимаемый жидкостью, Rв – реакция подвески на вес жидкости, весом оболочки пренебрегаем.
, где V – объём, занимаемый жидкостью, Rв – реакция подвески на вес жидкости, весом оболочки пренебрегаем.Рисунок 3





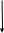




 R
R 
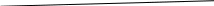
 r
r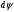
Px
Здесь нормальная нагрузка на оболочку состоит из постоянного давления наддува и переменного гидростатического давления. Пользуясь этим рисунком, следует определить Px и

Определение перемещений
-
Определение деформаций из физических соотношений
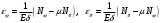 ,
,  - толщина оболочки
- толщина оболочки-
Для сферических полуднищ меридиональное и нормальное перемещения определяются из формул:
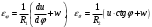
-
Для цилиндрической обечайки
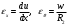
В результате интегрирования геометрических соотношений типа Коши, в решения для меридиональных перемещений войдут произвольные константы интегрирования, которые определяются из условий равенства меридиональных перемещений цилиндрической оболочки и полусферических днищ в зоне контакта, равенство нулю осевого перемещения цилиндрической оболочки в сечении закрепления, должно также выполняться условие равенства меридиональных усилий по линии стыка.
Построение эпюр
Построить эпюры перемещений и меридиональных усилий.
Краевой эффект в зоне верхнего стыка двух оболочек