Файл: Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Математика Практическое занятие 2.docx
Добавлен: 29.11.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проведем высоту h из вершины B.
h – это высота ∆ABC и ∆ABD.
Найдем высоту, используя формулу площади треугольника:
S∆=
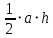
SABC=
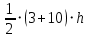
39=
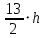
78=13⋅h
h=6 см
gрименим эту же формулу для ∆ABD:
SABD=
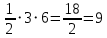 (см2)
(см2)Задание 6 (максимальное количество баллов – 4 балла)
Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.
Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500.
Решение:
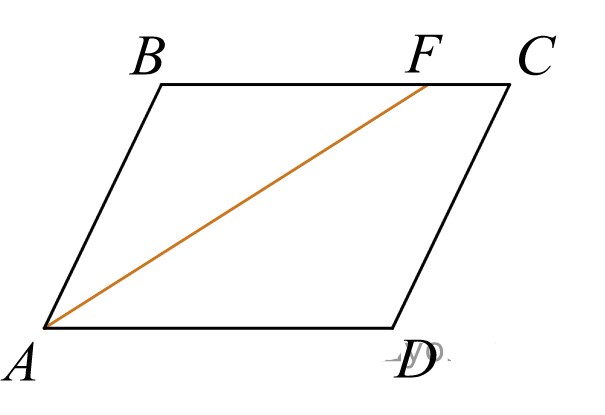
Накрест лежащие углы ∠BFA и ∠FAD равны, АF – биссектриса угла
 BAD, отсюда следует
BAD, отсюда следует 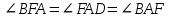
Значит ∆BFA – равнобедренный и AB=BF=4 см.
По формуле площади параллелограмма
S=a⋅b⋅sin(α)
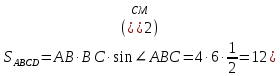
Задание 7 (максимальное количество баллов – 3 балла)
Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 см и 8 см, а боковое ребро призмы равно 12 см.
Решение:
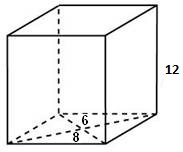
Диагонали ромба всегда пересекаются под прямым углом и делятся точкой пересечения пополам. Тогда, для того чтобы найти сторону ромба можно рассмотреть прямоугольный треугольник с катетами 6:2=3 и 8:2=4 и по теореме Пифагора имеем:
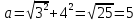 (см)
(см)Площади боковой грани будет равна:
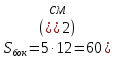
Площадь ромба:
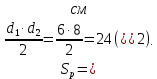
Таким образом,
площадь поверхности призмы равна
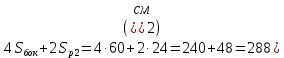
Пермь - 2023