МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ

«Национальный исследовательский технологический университет «МИСиС» в городе Алмалык


ГОРНО-МЕТАЛЛУРГИЧЕСКИЙ ФАКУЛЬТЕТ

Курсовая работа

по дисциплине: «Основы теории сигналов и систем»

Выполнила: студентка гр. 8-19 АТПП Гафуров С. О.

Дата сдачи: «___» ____________202___г.


Алмалык-2021

Для каких сигналов рационально применять аппроксимацию функциями Хаара?

Известно, что произвольный сигнал  , для которого выполняется условие   может быть представлен ортогональной системой функций  :

,                             (18)

коэффициенты определяются из соотношения

,

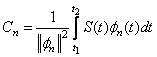где 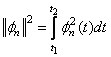  - квадрат нормы или энергия базисной функции  . Ряд (18) называется обобщенным рядом Фурье. При этом произведения вида 

---

, входящие в ряд (18), представляют собой спектральную плотность сигнала  , а коэффициенты   - спектр сигнала. Суть спектрального анализа сигнала   состоит в определении коэффициентов  . Зная эти коэффициенты возможен синтез (аппроксимация) сигналов при фиксированном числе   ряда:

.

Обобщенный ряд Фурье при заданной системе базисных функций   и числе слагаемых   он обеспечивает наилучший синтез по критерию минимума среднеквадратической ошибки  , под которой понимается величина

.

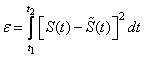Известные преобразования (Адамара, Карунена-Лоэва, Фурье) «плохо» представляют нестационарный сигнал в коэффициентах разложения. Покажем это на следующем примере. Пусть дана нестационарная функция

                          (19)

и ее преобразование Фурье (рис. 9).

Анализ рис. 9 показывает, что нестационарность временного сигнала   представляется большим числом высокочастотных коэффициентов отличных от нуля. При этом возникают следующие проблемы:

- сложно провести анализ временного сигнала по его Фурье образу;

- приемлемая аппроксимация временного сигнала возможна при учете большого числа высокочастотных коэффициентов;

---

- плохое визуальное качество реальных изображений восстановленных по низкочастотным коэффициентам; и т.п.

Существующие проблемы обусловили необходимость разработки математического аппарата преобразования нестационарных сигналов. Одним из возможных путей анализа таких сигналов стало вейвлет-преобразование (ВП).



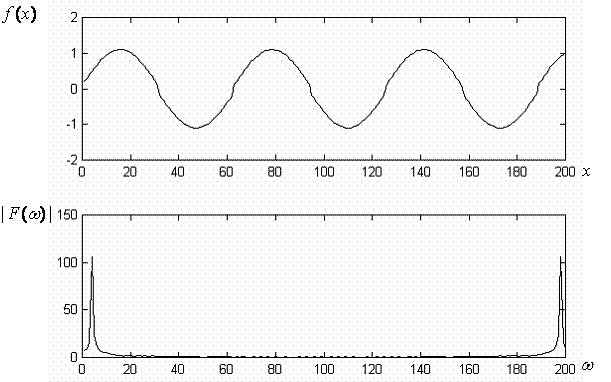
Рис. 9. Преобразование Фурье синусоидального сигнала с небольшими ступеньками при переходе через нуль

ВП одномерного сигнала – это его представление в виде обобщенного ряда Фурье или интеграла Фурье по системе базисных функций локализованных как в пространственной, так и в частотной областях. Примером такой базисной функции может служить вейвлет Хаара, который определяется выражением

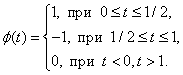                      (20)

Графически вейвлет Хаара представляется следующим образом:



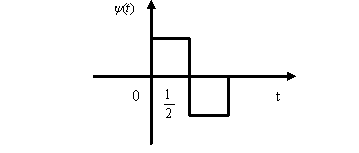
Рис. 10. Базисная функция вейвлета Хаара

Рассмотрим процесс разложения сигнала   в системе базисных функций Хаара. Первая базисная функция, в отличие от всех последующих, представляет собой прямую линию. В случае нормированного базиса  , свертка первой базисной функции с исходным сигналом будет определять его среднее значение. Пусть дан дискретный сигнал   длиной   отсчетов. Нормированная базисная функция на интервале   описывается выражением  . Тогда свертка данной функции с сигналом 

---

 приводит к выражению

.

Если выполнить синтез сигнала   по коэффициенту   с помощью синтезирующей функции  , получим постоянную составляющую, соответствующую среднему значению сигнала. Для того чтобы иметь возможность более детально описать сигнал, вычислим второй коэффициент с помощью базисной функции, представленной выражением (20):



Анализ данного выражения показывает, что коэффициент   характеризует разности средних значений половинок сигнала  . Если теперь выполнить синтез по двум коэффициентам с синтезирующей базисной функцией для второго коэффициента



получим следующую аппроксимацию:



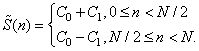
Дальнейшая операция анализа, т.е вычисления коэффициентов   и синтеза аналогична рассмотренной, с той разницей, что все действия повторяются для половинок сигнала, затем для четверти, и т.д. На самой последней итерации анализ осуществляется для пар случайных величин (рис 11).



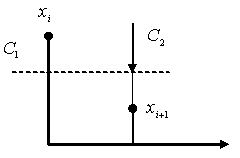
Рис. 11. Преобразование пар случайных величин

В результате исходный сигнал точно описывается коэффициентами вейвлет-преобразования Хаара. Вейвлет-коэффициенты сигнала (19) показаны на рис. 10.

---

Из приведенного рисунка видно, что нестационарности сигнала (резкие перепады) локализуются в малом числе вейвлет-коэффициентов. Это приводит к возможности лучшего восстановления нестационарного сигнала по неполным данным.

 



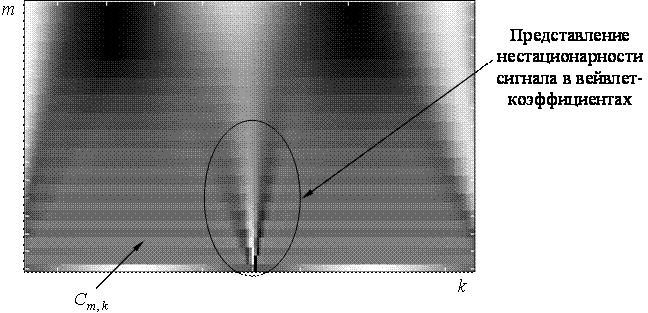
Рис. 12. Вейвлет-коэффициенты одного периода функции (19)

При вычислении вейвлет-коэффициентов   базисные функции покрывали анализируемый сигнал следующим образом (рис. 12). Из рис. 12 видно, что система базисных функций Хаара в дискретном пространстве должна задаваться двумя параметрами: сдвига и частоты (масштаба):

,

где   - масштаб базисной функции;   - сдвиг. В дискретном случае параметр масштаба  , где   - любое целое положительное число, параметр сдвига  . Таким образом, все множество базисных функций можно записать как

.

Прямое и обратное дискретные ВП вычисляются по формулам

,

.

Следует  отметить, что если число отсчетов  , то максимальное значение   равно 

---

Смотрите также файлы

• Методические указания Рекомендовано Научнометодическим советом университета для студентов, обучающихся по направлению Психология Ярославль 2011.pdf

• Практическая работа по дисциплине Психология, Фоменко Андрей Владимирович.pdf

• Льтет экономики, управления и юриспруденции Каф.docx

• Статья 74 Конституции рф формулирует два принципиальных для таможенного дела и таможенного права положения вопервых, на территории Российской Федерации запрещено устанавливать таможенные границы, пошлины, сборы и какиелибо иные препятствия для свободного .docx

• S. T. Gladding ccoouu.pdf