ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Наибольшее значение 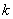 для текущего
для текущего  равно
равно 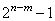 .
.
Для непрерывных сигналов будут справедливы следующие интегральные выражения:
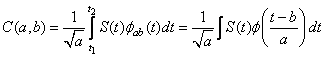 ,
,
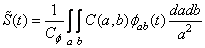 .
.
Таким образом, задавая вейвлет-функции, можно выполнять разложение сигнала по вейвлет-базису непрерывных или дискретных сигналов.
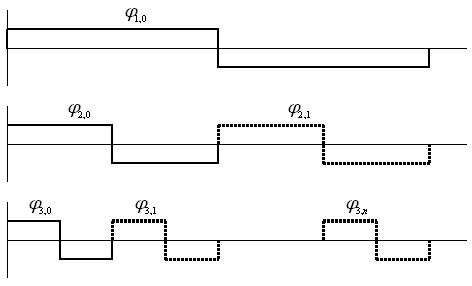
Рис. 13. Распределение базисных функций Хаара при анализе сигнала
Функция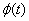 может образовывать вейвлет-базис, если она удовлетворяет следующим условиям:
может образовывать вейвлет-базис, если она удовлетворяет следующим условиям:
1. Ограниченность нормы:
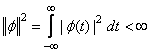 .
.
2. Вейвлет-функция должна быть ограничена и по времени и по частоте:
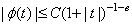 и
и 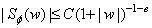 , при
, при 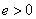 .
.
Контрпример: дельта-функция и гармоническая функция не удовлетворяют данному условию.
3. Нулевое среднее:
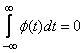 .
.
Если обобщить данное условие, то можно получить формулу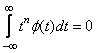 , которая определяет степень гладкости функции
, которая определяет степень гладкости функции 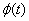 . Считается, что чем выше степень гладкости базисной функции, тем лучше ее аппроксимационные свойства.
. Считается, что чем выше степень гладкости базисной функции, тем лучше ее аппроксимационные свойства.
В качестве примера приведем следующие известные вейвлет-функции:
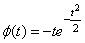 ,
, 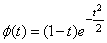 .
.
Для ВП, также как и для ДПФ существует алгоритм быстрого преобразования. Рассмотрим снова ВП Хаара. Из рис. 13 видно, что функции с малым масштабным коэффициентом используют те же отсчеты сигнала для вычисления коэффициентов, что и функции с большим масштабным коэффициентом. При этом операция суммирования одних и тех же отсчетов повторяется неоднократно. Следовательно, для уменьшения объема вычислений целесообразно вычислять ВП с самого малого масштабного коэффициента. В результате получаем вейвлет-коэффициенты, представляющие собой средние значения
используют те же отсчеты сигнала для вычисления коэффициентов, что и функции с большим масштабным коэффициентом. При этом операция суммирования одних и тех же отсчетов повторяется неоднократно. Следовательно, для уменьшения объема вычислений целесообразно вычислять ВП с самого малого масштабного коэффициента. В результате получаем вейвлет-коэффициенты, представляющие собой средние значения 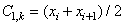 и разности
и разности 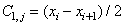 . Для коэффициентов
. Для коэффициентов 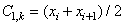 повторяем данную процедуру. При этом усреднение коэффициентов
повторяем данную процедуру. При этом усреднение коэффициентов 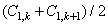 будет соответствовать усреднению четырех отсчетов сигнала, но при этом расходуется одна операция умножения и одна операция сложения. Процесс разложения повторяется до тех пор, пока не будут вычислены все коэффициенты спектра
будет соответствовать усреднению четырех отсчетов сигнала, но при этом расходуется одна операция умножения и одна операция сложения. Процесс разложения повторяется до тех пор, пока не будут вычислены все коэффициенты спектра  .
.
Запишем алгоритм быстрого вейвлет-преобразования Хаара в матричном виде. Пусть дан вектор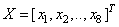 размером 8 элементов. Матрица преобразования Хаара запишется в виде
размером 8 элементов. Матрица преобразования Хаара запишется в виде
 ,
,
В приведенных обозначениях один шаг быстрого ВП запишется как
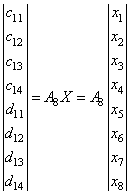 . (21)
. (21)
Повторяем операцию преобразования для коэффициентов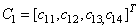 :
:
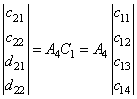 , (22)
, (22)
для коэффициентов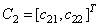
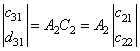 . (23)
. (23)
В результате получается набор вейвлет-коэффициентов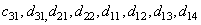 , по которым можно точно восстановить исходный сигнал. Для этого необходимо задать матрицу синтеза
, по которым можно точно восстановить исходный сигнал. Для этого необходимо задать матрицу синтеза 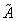
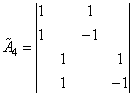 ,
, 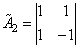 .
.
Восстановленный сигнал запишется в виде
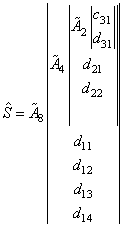 . (24)
. (24)
В общем случае вместо коэффициентов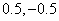 могут быть любые другие, которые описывают соответствующее ВП. При этом элементы в матрицах
могут быть любые другие, которые описывают соответствующее ВП. При этом элементы в матрицах 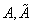 можно характеризовать как коэффициенты низко- и высокочастотных фильтров анализа и синтеза соответственно:
можно характеризовать как коэффициенты низко- и высокочастотных фильтров анализа и синтеза соответственно:
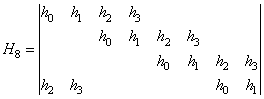 ,
,
 ,
,
где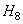 - матрица выделения низкочастотных составляющих;
- матрица выделения низкочастотных составляющих;
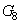 - матрица выделения высокочастотных составляющих. При этом преобразование сигнала можно представить через свертку КИХ-фильтров (рис. 14).
- матрица выделения высокочастотных составляющих. При этом преобразование сигнала можно представить через свертку КИХ-фильтров (рис. 14).
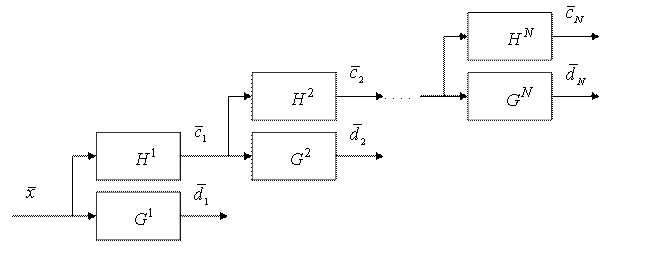
Рис. 14. Представление ВП через набор низко- и высокочастотных фильтров
Обобщение ВП на двумерный случай приводит к разделимому преобразованию:
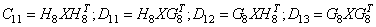 ,
,
где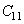 - низкочастотная составляющая;
- низкочастотная составляющая; 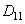 ,
, 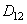 ,
, 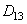 - высокочастотные составляющие. Таким образом, при двумерном ВП изображение разбивается на четыре компоненты: три высокочастотные, представляющие мелкие детали, и одна низкочастотная, представляющая собой уменьшенную и сглаженную копию исходного изображения. В соответствии с алгоритмом БВП второй шаг ВП запишется в виде
- высокочастотные составляющие. Таким образом, при двумерном ВП изображение разбивается на четыре компоненты: три высокочастотные, представляющие мелкие детали, и одна низкочастотная, представляющая собой уменьшенную и сглаженную копию исходного изображения. В соответствии с алгоритмом БВП второй шаг ВП запишется в виде
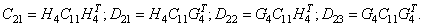
В результате получаем представление изображения на разных уровнях масштаба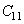 ,
, 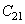 , и т.д. Операции преобразования сигнала можно рекуррентно выполнять, пока низкочастотная составляющая не будет представлена одним отсчетом.
, и т.д. Операции преобразования сигнала можно рекуррентно выполнять, пока низкочастотная составляющая не будет представлена одним отсчетом.
Расчет ортогональных вейвлет-фильтров
Рассмотрим матричный способ расчета вейвлет-фильтров для преобразования сигнала. Допустим, что низко- и высокочастотные коэффициенты фильтров ортогональны друг другу. В этом случае можно записать
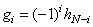
,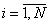 . (25)
. (25)
где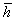 – коэффициенты низкочастотного фильтра;
– коэффициенты низкочастотного фильтра; 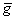 – высокочастотного. Запишем матрицу преобразования
– высокочастотного. Запишем матрицу преобразования 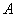 размером 8х8 элементов, при длине вейвлет-фильтров
размером 8х8 элементов, при длине вейвлет-фильтров 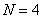 :
:
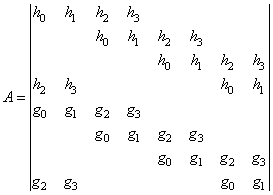 .
.
В соответствии с третьим условием базисных вейвлет-функций потребуем наличия 2-х нулевых моментов:
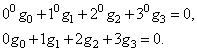
Для того чтобы преобразование было обратимым, необходимо выполнение условия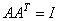 , где
, где 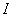 – единичная матрица. В результате получаем еще два уравнения:
– единичная матрица. В результате получаем еще два уравнения:
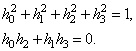
Решение полученной системы уравнений даст коэффициенты низкочастотного фильтра:
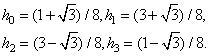
Коэффициенты высокочастотного фильтра находятся из уравнения (25).
Вычисленные ортогональные вейвлеты получили название вейвлетов Добеши. Другим видом ВП является биортогональное преобразование. В этом случае базисные функции анализа не ортогональны друг другу. При этом удается получить вейвлет-фильтры с большим числом нулевых моментов.
Для непрерывных сигналов будут справедливы следующие интегральные выражения:
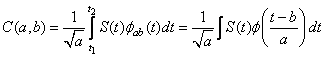 ,
,Таким образом, задавая вейвлет-функции, можно выполнять разложение сигнала по вейвлет-базису непрерывных или дискретных сигналов.

Рис. 13. Распределение базисных функций Хаара при анализе сигнала
Функция
1. Ограниченность нормы:
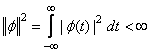 .
.2. Вейвлет-функция должна быть ограничена и по времени и по частоте:
Контрпример: дельта-функция и гармоническая функция не удовлетворяют данному условию.
3. Нулевое среднее:
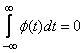 .
.Если обобщить данное условие, то можно получить формулу
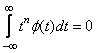 , которая определяет степень гладкости функции
, которая определяет степень гладкости функции В качестве примера приведем следующие известные вейвлет-функции:
Для ВП, также как и для ДПФ существует алгоритм быстрого преобразования. Рассмотрим снова ВП Хаара. Из рис. 13 видно, что функции с малым масштабным коэффициентом
Запишем алгоритм быстрого вейвлет-преобразования Хаара в матричном виде. Пусть дан вектор
 ,
,В приведенных обозначениях один шаг быстрого ВП запишется как
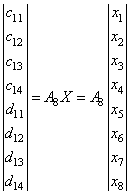 . (21)
. (21)Повторяем операцию преобразования для коэффициентов
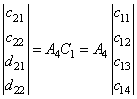 , (22)
, (22)для коэффициентов
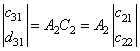 . (23)
. (23)В результате получается набор вейвлет-коэффициентов
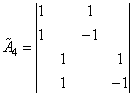 ,
, Восстановленный сигнал запишется в виде
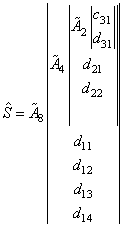 . (24)
. (24)В общем случае вместо коэффициентов
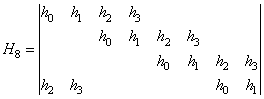 ,
, ,
,где

Рис. 14. Представление ВП через набор низко- и высокочастотных фильтров
Обобщение ВП на двумерный случай приводит к разделимому преобразованию:
где
В результате получаем представление изображения на разных уровнях масштаба
Расчет ортогональных вейвлет-фильтров
Рассмотрим матричный способ расчета вейвлет-фильтров для преобразования сигнала. Допустим, что низко- и высокочастотные коэффициенты фильтров ортогональны друг другу. В этом случае можно записать
,
где
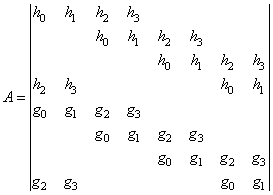 .
.В соответствии с третьим условием базисных вейвлет-функций потребуем наличия 2-х нулевых моментов:
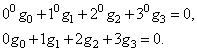
Для того чтобы преобразование было обратимым, необходимо выполнение условия
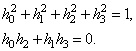
Решение полученной системы уравнений даст коэффициенты низкочастотного фильтра:
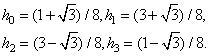
Коэффициенты высокочастотного фильтра находятся из уравнения (25).
Вычисленные ортогональные вейвлеты получили название вейвлетов Добеши. Другим видом ВП является биортогональное преобразование. В этом случае базисные функции анализа не ортогональны друг другу. При этом удается получить вейвлет-фильтры с большим числом нулевых моментов.