Файл: Лабораторная работа Моделирование оптимизационных задач.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 47
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа
Моделирование оптимизационных задач
методами линейного программирования
Цель работы: изучить практические методы моделирования типичных экономических задач методами линейного программирования с применением электронных таблиц и математического процессора.
Теоретическая часть
Линейное программирование (ЛП) — это раздел математики, занимающийся решением таких задач на отыскание наибольших и наименьших значений, для которых методы математического анализа оказываются непригодными. Другими словами термин «линейное программирование» характеризует определение программы (плана) работы конкретного экономического объекта на основе выявления линейных связей между его элементами. Задачей линейного программирования является нахождение оптимального, т. е. наилучшего, плана при заданной системе налагаемых на решение ограничений.
К классу задач линейного программирования относится большое количество разнообразных задач планирования и управления, как, например:
-
нахождение оптимального плана выпуска продукции (оптимальное распределение ресурсов); -
оптимизация межотраслевых потоков (планирование производства различных видов продукции по отраслям); -
определение оптимального рациона (оптимизация состава химической смеси); -
транспортная задача (оптимальное распределение потоков товарных поставок по транспортной сети); -
задача о размещении производства (планирование с учётом затрат на производство и транспортировку продукции); -
задача о назначениях (оптимальное распределение различных видов транспортных средств) и др.
Задачей линейного программирования является задача оптимизации (т. е. максимизации или минимизации) линейной функции
при наличии линейных ограничений
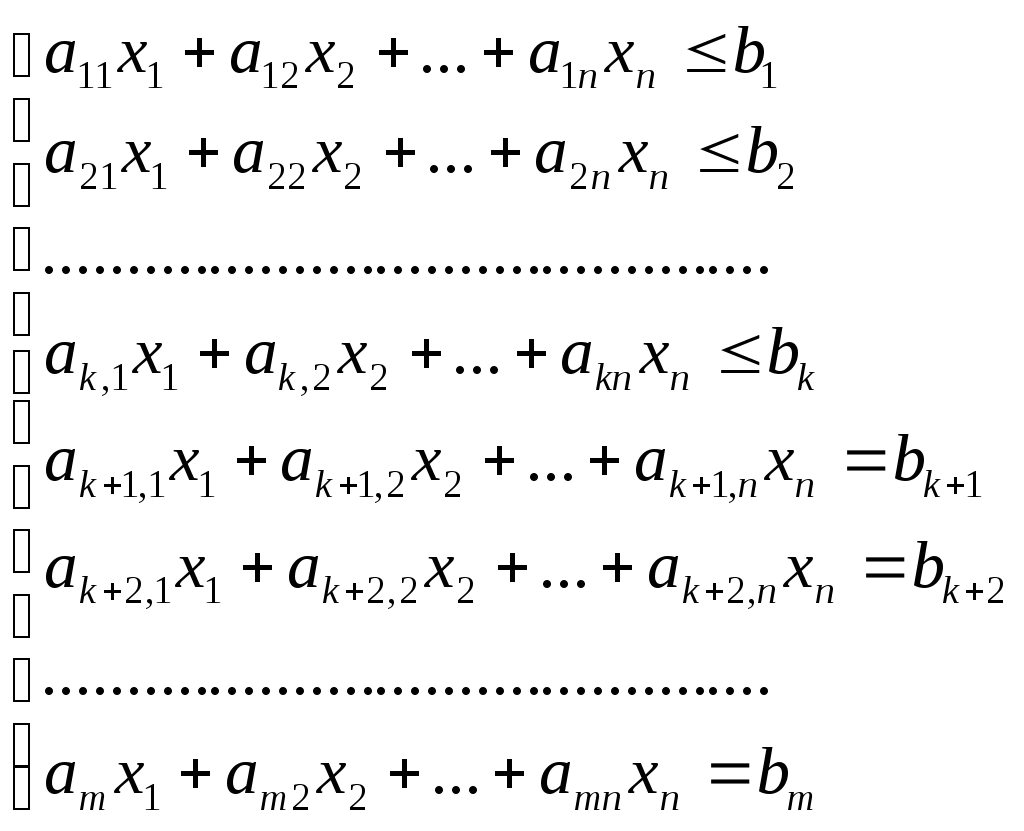 (2)
(2),
Другими словами, необходимо найти такое решение
В этой задаче число неизвестных
Общая формулировка задания
Перед выполнением лабораторной работы изучите теоретическую часть, последовательно выполните все указанные в контрольном примере действия, оформите отчет.
Пример выполнения работы
1 Задача об оптимальном составе смеси (задача составления рациона, задача о диете)
К группе задач о смесях относят задачи по нахождению наиболее экономичного набора из определённых ингредиентов (пищевых продуктов, руды, нефти и др.), обеспечивающих получение смеси с заданными свойствами (ограничения на физический или химический состав смеси и на наличие необходимых материалов). Иными словами, получаемые смеси должны иметь в своём составе
Задача 1. Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33-х единиц питательного вещества
Таблица 1
| |
| |
| Стоимость (руб.) |
| Весовая единица корма I | 4 | 3 | 1 | 20 |
| Весовая единица корма II | 3 | 2 | 1 | 20 |
| Весовая единица корма III | 2 | 1 | 2 | 10 |
Требуется составить наиболее дешёвый рацион, при котором каждое животное получило бы необходимые количества питательных веществ
Математическая постановка задачи 1. Пусть
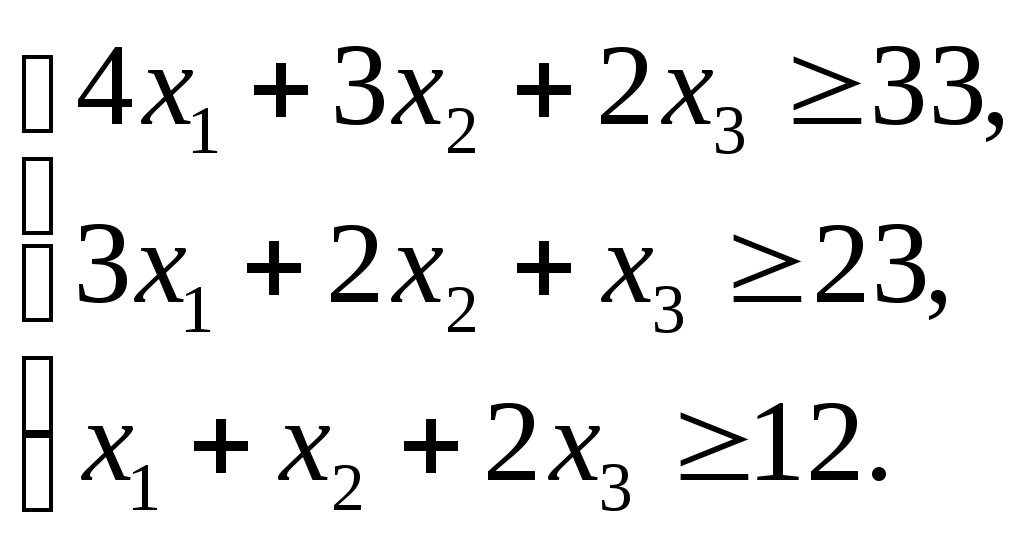 (3)
(3)При этом линейная функция (стоимость рациона)
Решение задачи 1 в среде MicrosoftExcel.
В настоящее время одним из наиболее известных способов численного решения задач линейного программирования является использование надстройки «Поиск решения» электронных таблиц Microsoft Excel.
Теоретической основой надстройки «Поиск решения» является симплекс-метод, позволяющий находить оптимальное решение задачи планирования с помощью итерационного процесса перехода к улучшающимся планам. «Поиск решения» является дополнением Excel, т. е. может не входить в стандартный вариант установки электронных таблиц. Для его добавления достаточно воспользоваться командой ФайлПараметрыНадстройкиПоиск решения.
При решении задачи с помощью надстройки Поиск решения необходимо:
-
открыть окно Microsoft Excel и активизировать надстройку; -
заполнить ячейкиA1-А4 таблицы обозначениями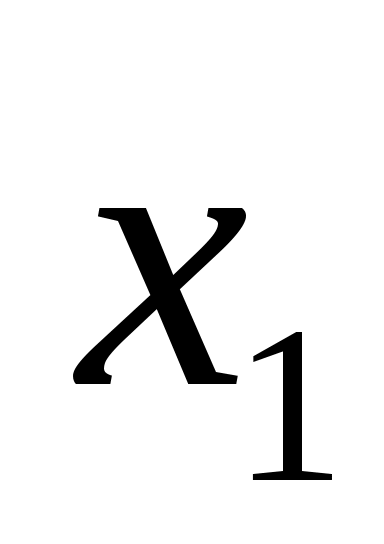 ,
, 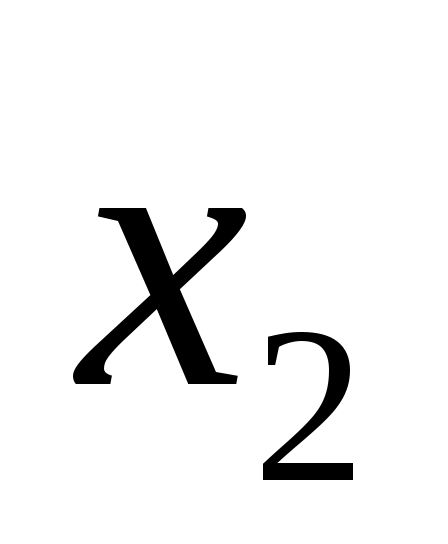 ,
, 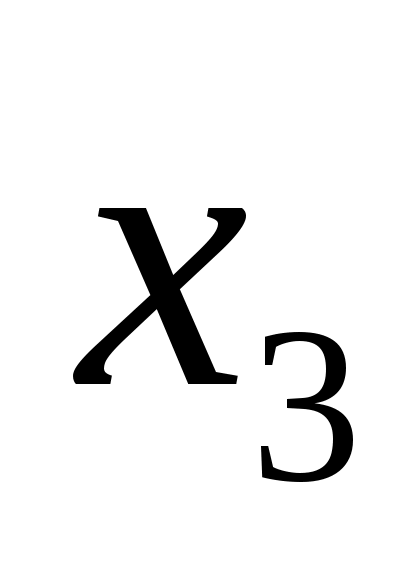 и min соответственно. В ячейку В4 записать формулу (4) через адреса соответствующих ячеек
и min соответственно. В ячейку В4 записать формулу (4) через адреса соответствующих ячеек 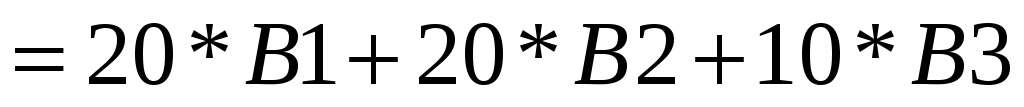 (адреса ячеек вводятся щелчком мыши по соответствующей ячейке или набираются с клавиатуры) (рисунок 1);
(адреса ячеек вводятся щелчком мыши по соответствующей ячейке или набираются с клавиатуры) (рисунок 1);
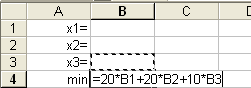
Рисунок 1- Ввод целевой функции
-
в диапазон ячеек А7-С9 записать систему (3) через адреса соответствующих ячеек, т. е. в А7 ввести формулу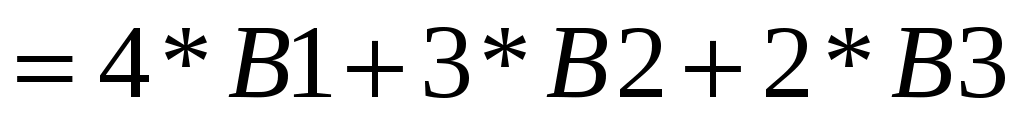 , нажать Enter, в А8 ввести формулу
, нажать Enter, в А8 ввести формулу 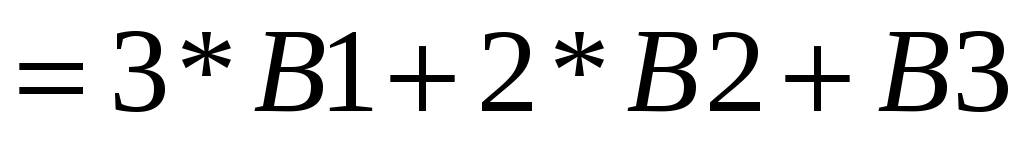 , нажать Enter, в А9 ввести формулу
, нажать Enter, в А9 ввести формулу 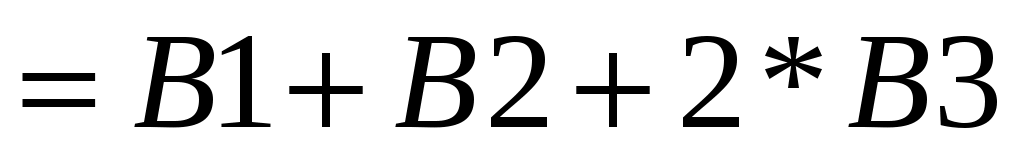 , нажать Enter, в ячейки В7-В9 ввести слова «не менее», в ячейки С7-С9 значения соответственно рисунку 2;
, нажать Enter, в ячейки В7-В9 ввести слова «не менее», в ячейки С7-С9 значения соответственно рисунку 2;
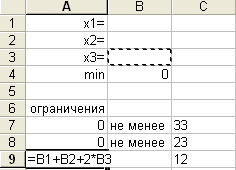
Рисунок 2- Ввод ограничений
-
для решения поставленной задачи в меню выбрать пункт Поиск решения… (рисунок 3). В появившемся окне Выбор метода решения установите Поиск решения линейных задач симплекс-методом;
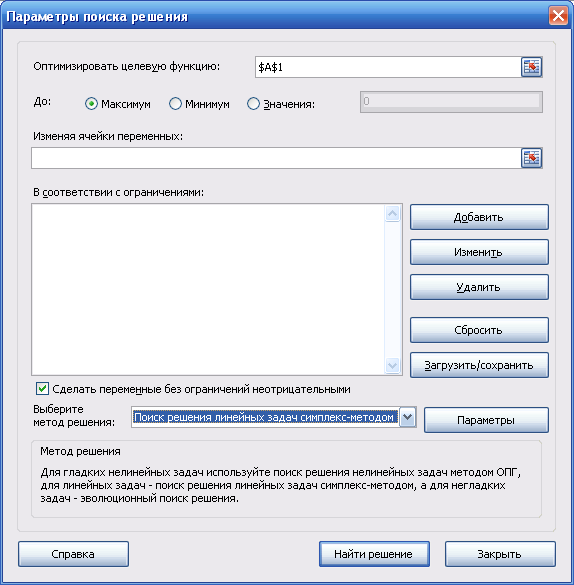
Рисунок 3 – Параметры поиска решения
-
в окне Параметры поиска решения в поле Оптимизировать целевую функцию щёлкните по кнопке , затем в ячейке B4 и снова по кнопке
, затем в ячейке B4 и снова по кнопке  ; в поле До установить флажок Минимум, в поле Изменяя ячейки переменных щёлкнуть по кнопке
; в поле До установить флажок Минимум, в поле Изменяя ячейки переменных щёлкнуть по кнопке  , выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке
, выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке  ;
; -
в этом же окне осталось незаполненным поле В соответствии с ограничениями, поэтому надо нажать на копку Добавить: появится новое окно Добавление ограничения, в поле Ссылка на ячейку щёлкнуть по кнопке , затем выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке
, затем выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке  , в следующем поле необходимо выбрать знак >=, нажав
, в следующем поле необходимо выбрать знак >=, нажав  , затем в поле Ограничение ввести 0 (рисунок 4);
, затем в поле Ограничение ввести 0 (рисунок 4);
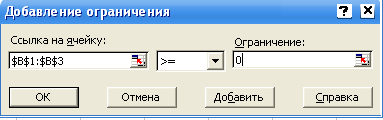
Рисунок 4 – Добавление первого ограничения
-
в этом же окне Добавление ограничения нажать кнопку Добавить (появится новое окно Добавление ограничения) и ввести новое ограничение: в поле Ссылка на ячейку надо щёлкнуть по кнопке , затем выделить мышью диапазон ячеек А7А9 и снова щёлкнуть по кнопке
, затем выделить мышью диапазон ячеек А7А9 и снова щёлкнуть по кнопке  , в следующем поле необходимо выбрать знак >=, нажав
, в следующем поле необходимо выбрать знак >=, нажав  , затем в поле Ограничение надо щёлкнуть по кнопке
, затем в поле Ограничение надо щёлкнуть по кнопке  , затем выделить мышью диапазон ячеек C7C9 и снова щёлкнуть по кнопке
, затем выделить мышью диапазон ячеек C7C9 и снова щёлкнуть по кнопке  ( рисунок 5);
( рисунок 5);
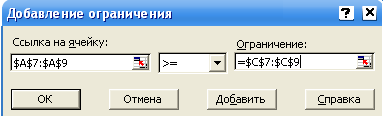
Рисунок 5 - Добавление ограничения
-
теперь все ограничения учтены: надо нажать ОК, после чего снова откроется диалоговое окно Поиск решения, и надо нажать кнопку Выполнить. В появившемся диалоговом окне Результаты поиска решения (в котором компьютер предлагает по умолчанию сохранить найденное решение) надо нажать кнопку ОК. -
Результат полученных вычислений представлен на рисунке 8.
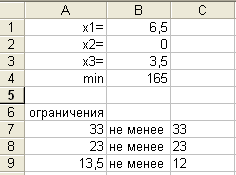
Рисунок 6 - Результат подбора значений
Замечание 1. Если в неравенствах (3) знаки разные (
Замечание 2. Если часть ограничений представляют собой неравенства другого знака (в данном случае
Замечание 3. На практике часто требуется, чтобы на переменные