Файл: Лабораторная работа Моделирование оптимизационных задач.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,  ,
,  налагалось условие целочисленности (например, если какой-то продукт нельзя разрезать на части, а можно добавлять в рацион только целыми порциями), в этом случае в окне Добавление ограничения, в поле Ссылка на ячейку надо щёлкнуть по кнопке
налагалось условие целочисленности (например, если какой-то продукт нельзя разрезать на части, а можно добавлять в рацион только целыми порциями), в этом случае в окне Добавление ограничения, в поле Ссылка на ячейку надо щёлкнуть по кнопке  , затем выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке
, затем выделить мышью диапазон ячеек В1В3 и снова щёлкнуть по кнопке  , в следующем поле необходимо выбрать условие ЦЕЛ, нажав
, в следующем поле необходимо выбрать условие ЦЕЛ, нажав  ( рисунок 7).
( рисунок 7).
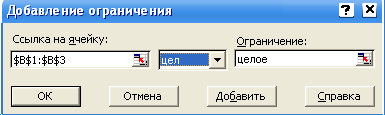
Рисунок 7 - Окно Добавление ограничения
Решение задачи 1 в среде MathСad:
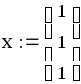
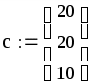
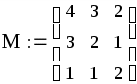
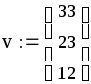
знак «присваивания» := находится на панели инструментов Вычисления; матрица (вектор) вставляется комбинацией клавиш Ctrl и M (англ.) или выбирается на панели инструментов Матрица, после чего вводятся количество строк и столбцов;
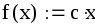
знак «умножить» вставляется комбинацией клавиш Shift и *;
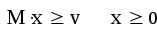
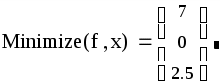
знак равенства вставляется с клавиатуры клавишей =;
после чего получим оптимальный план
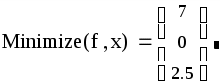
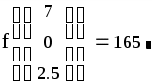
Таким образом, оптимальные планы Задачи 1 при решении в средах Microsoft Excel и MathСad получились различные (могут использоваться и те и другие), но целевая функция при этом имеет одинаковое значение.
Задача 2. В баре имеются три компонента: коньяк, шампанское, сок. Цель: подобрать оптимальный состав коктейля из этих трёх компонентов, если известно: стоимости ингредиентов в рублях: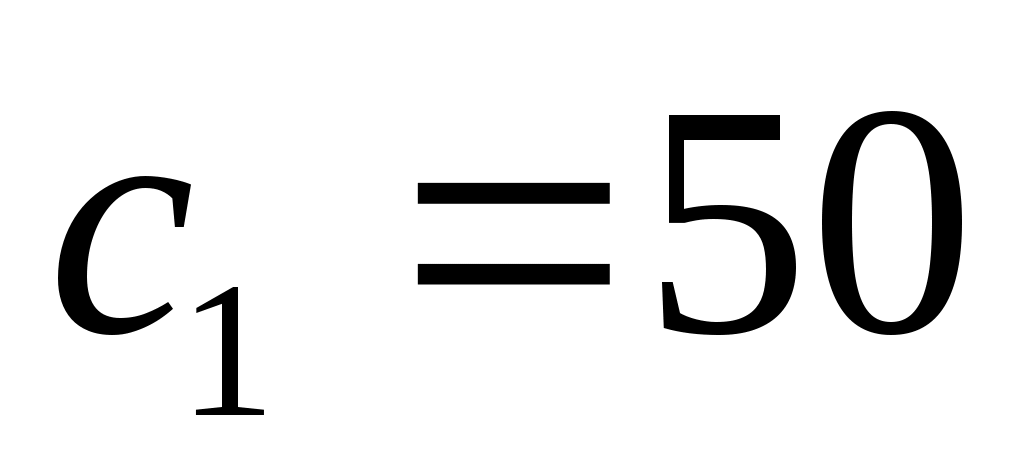 ,
, 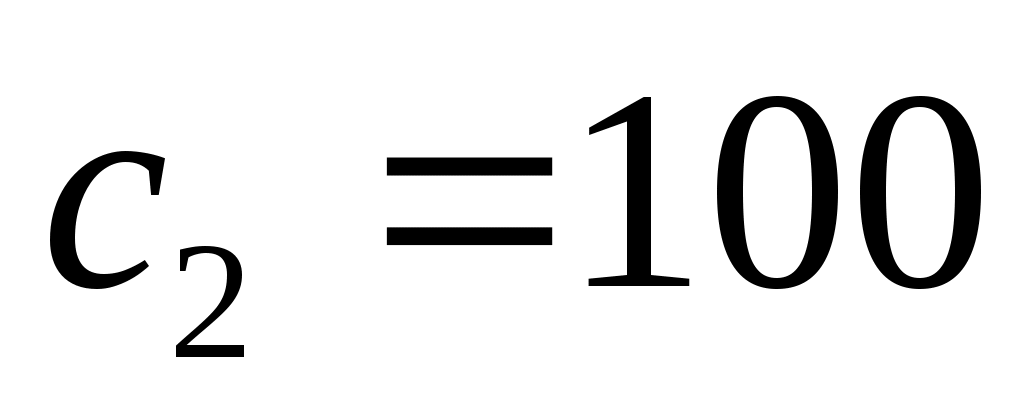 ,
, 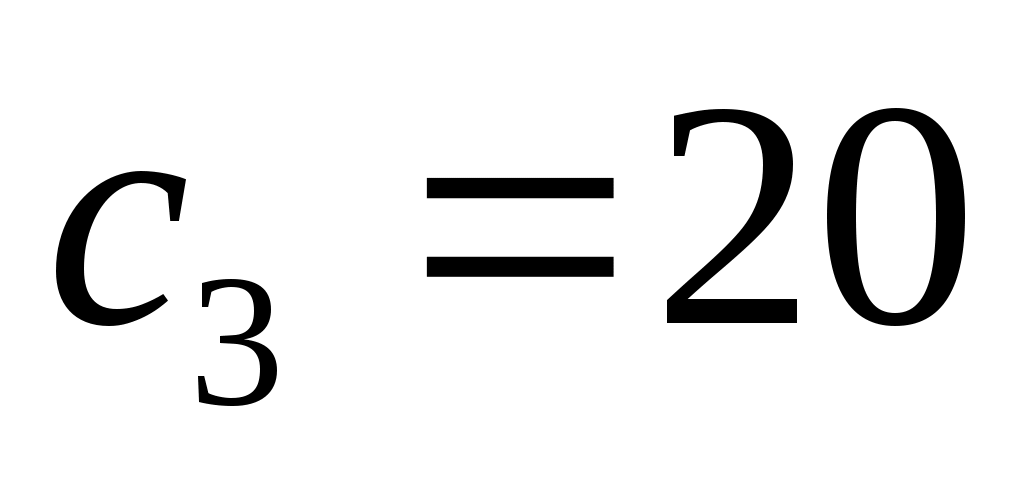 ; содержание алкоголя в промиллях
; содержание алкоголя в промиллях 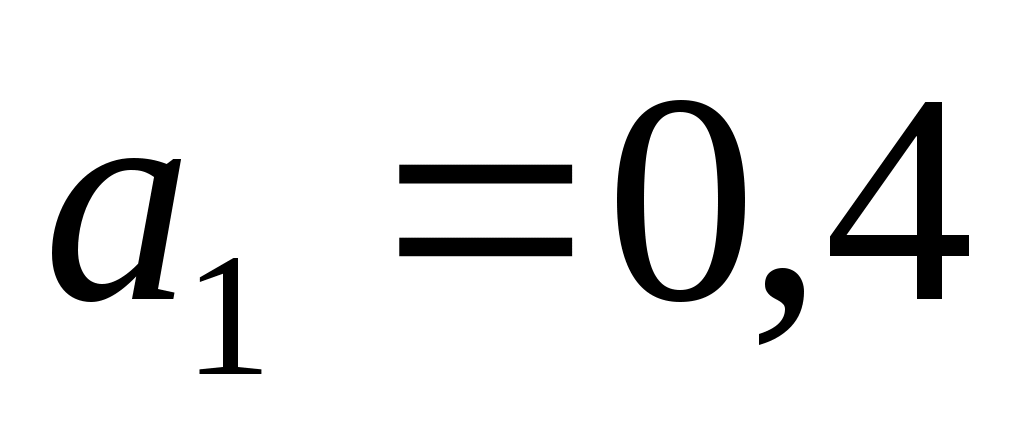 ,
, 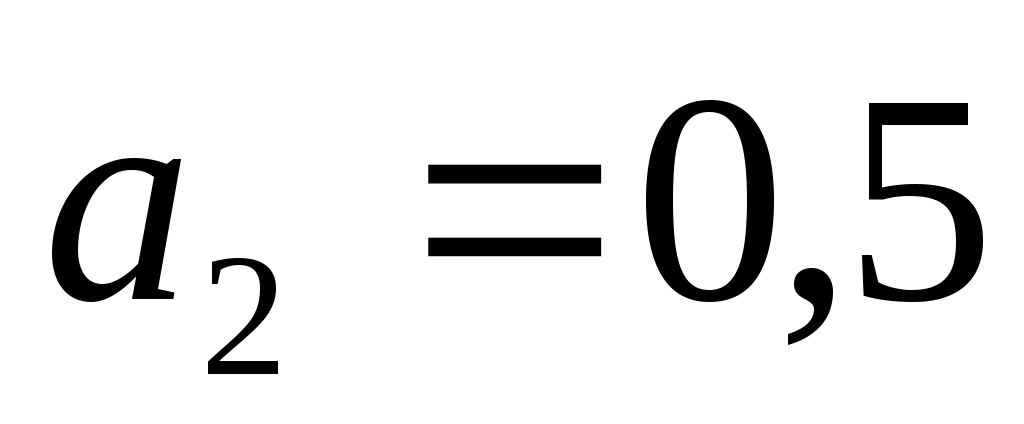 ,
, 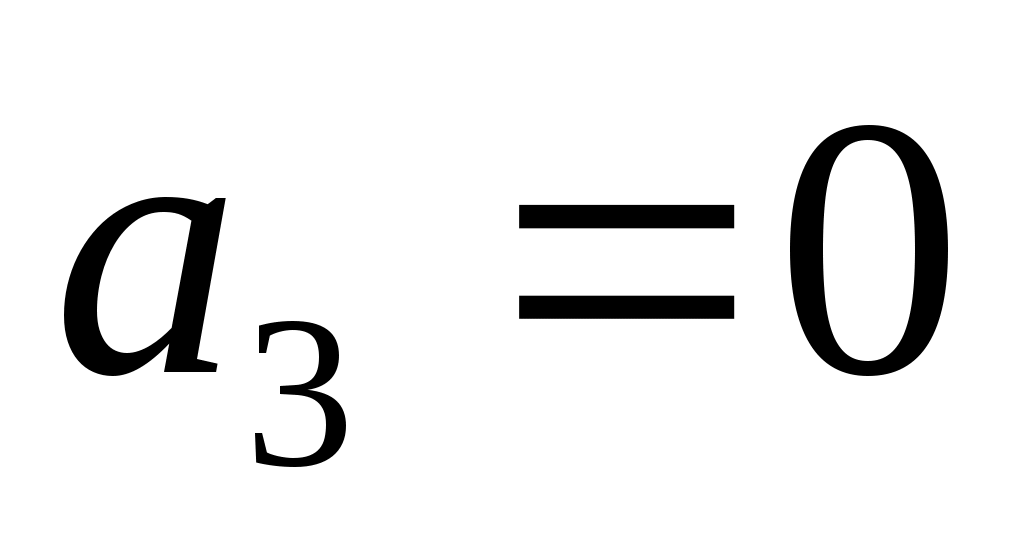 ; вкусовые качества в баллах
; вкусовые качества в баллах 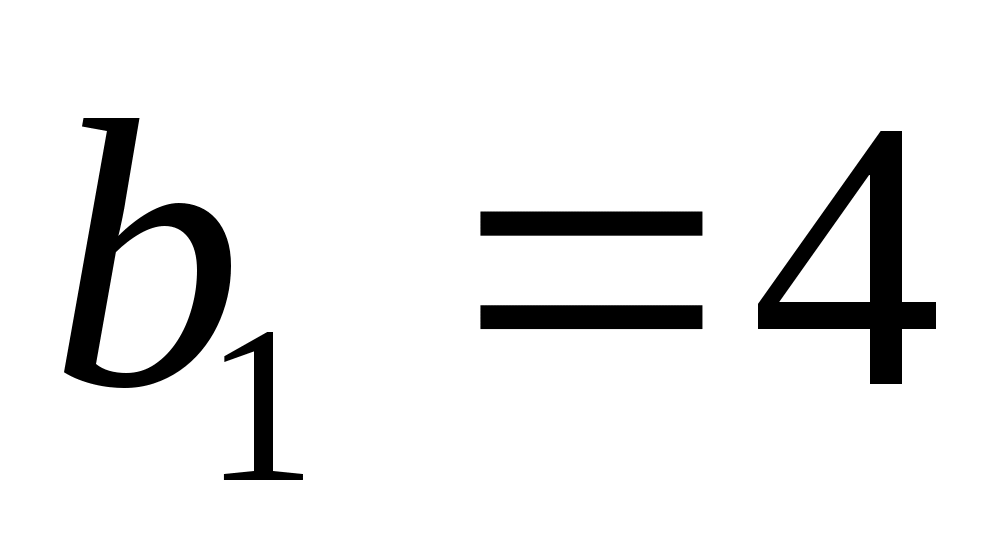 ,
, 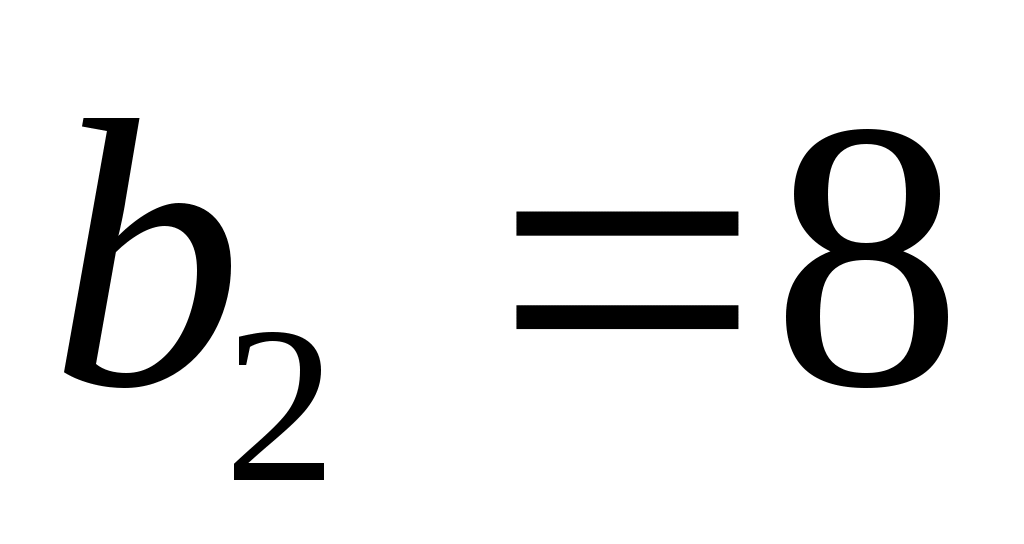 ,
, 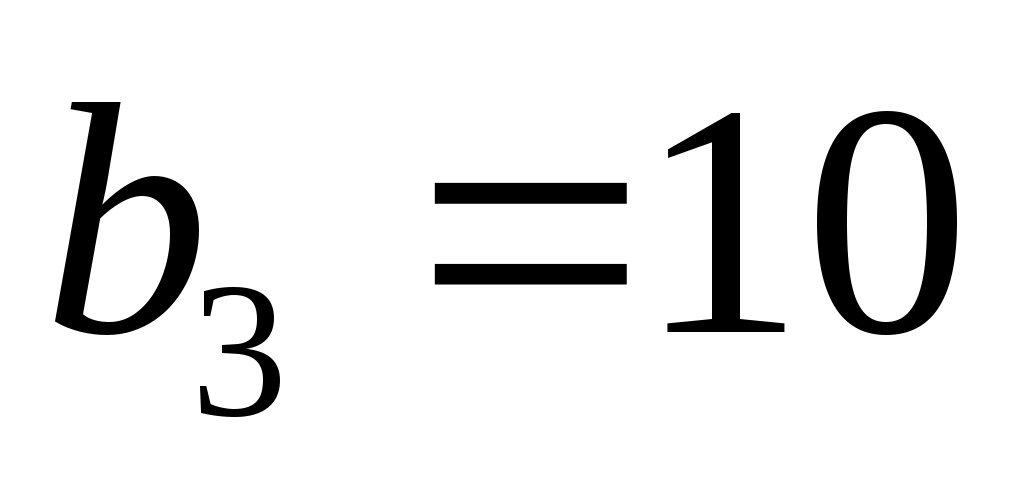 . Крепость коктейля должна быть не меньше 0,2 промилле. Вкус должен иметь не менее 8 баллов.
. Крепость коктейля должна быть не меньше 0,2 промилле. Вкус должен иметь не менее 8 баллов.
Математическая постановка задачи 2. Пусть ,
,  ,
,  — доля каждого компонента в коктейле (
— доля каждого компонента в коктейле ( ,
,  ).
).
Тогда должно быть:
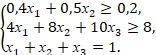 (5)
(5)
(третье условие отражает наличие в составе смеси только трёх компонентов, т. е. то, что все три компонента составляют весь коктейль в целом — 1).
При этом линейная функция (стоимость коктейля) будет иметь вид:
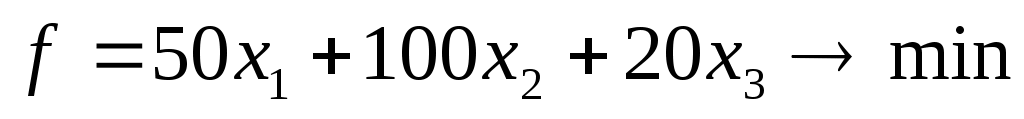 (6)
(6)
Решение задачи 2 в Microsoft Excel имеет вид, представленный на рисунке 8 и 9.
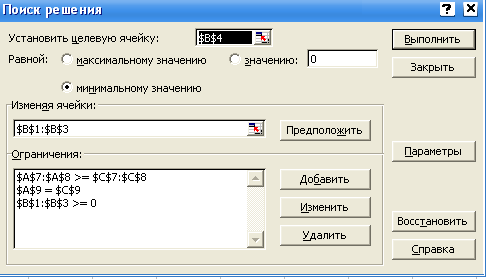
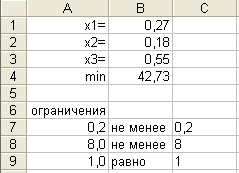
Рисунок 8 – Окно с поиском решения Рисунок 9- Решение
Замечание 5. Для того, чтобы в решении задачи после запятой отображалось только 2 знака, надо выделить соответствующий диапазон ячеек, щёлкнуть на выделенном правой кнопкой мыши, в появившемся контекстном меню выбрать пункт Формат ячеек и на вкладке Число выбрать Числовой, указав Число десятичных знаков 2.
Решение задачи 2 в среде MathСad:
Получен оптимальный план
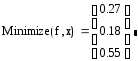
Для того чтобы MathСad отображал только 2 десятичных знака, надо выделить значения, для которых необходимо сменить формат вывода, в меню Формат выбрать подменю Результат — появится диалоговое окно Формат результата (рисунок 10) и указать количество десятичных знаков 2:
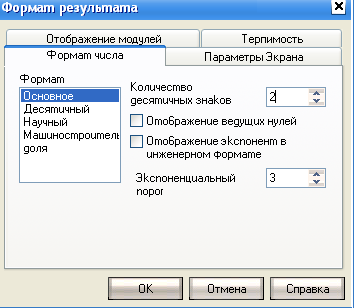
Рисунок 10 - Диалоговое окно Формат результата
Для вычисления значения целевой функции в точке минимума:
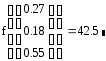
Таким образом, оптимальные планы Задачи 2 при решении в средах Microsoft Excel и MathСad получились одинаковые, а целевая функция при решении в среде MathСad имеет меньшее значение, таким образом, среда MathСad, в данном случае, даёт лучшее решение, чем Microsoft Excel.
3. Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
К группе задач о распределении ресурсов относят задачи, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время, затрачиваемое на неё и др., либо некоторая комбинация вышеперечисленного. В простейшем виде это задача о перевозках (транспортная задача).
Задача 3. На товарных станциях и
и 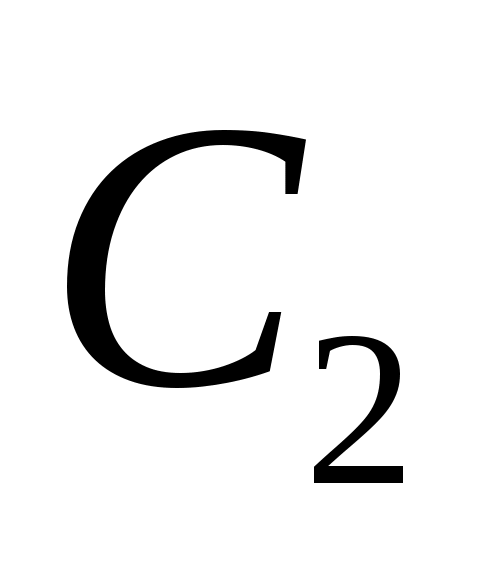 имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции
имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции 
в магазины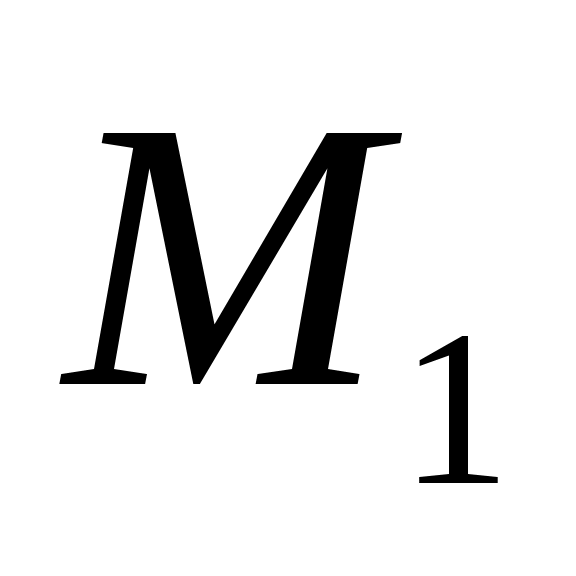 ,
, 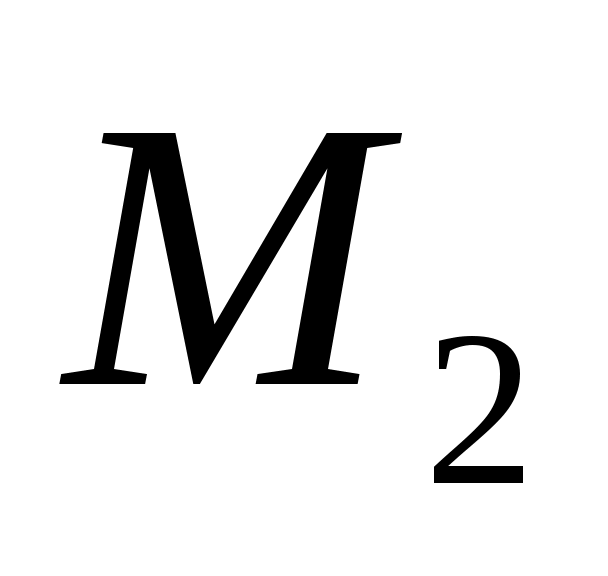 ,
, 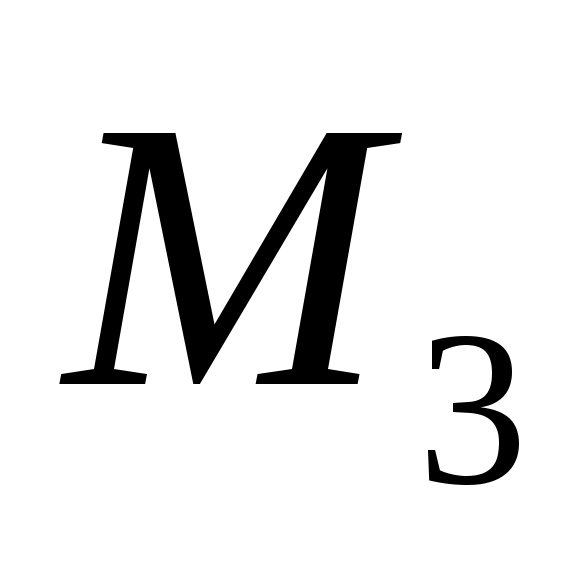 стоит 1 руб., 3 руб., 5 руб. соответственно, а стоимость перевозки со станции
стоит 1 руб., 3 руб., 5 руб. соответственно, а стоимость перевозки со станции  в те же магазины – 2 руб., 5 руб., 4 руб. необходимо доставить в каждый магазин по 20 комплектов мебели. Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими.
в те же магазины – 2 руб., 5 руб., 4 руб. необходимо доставить в каждый магазин по 20 комплектов мебели. Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими.
Математическая постановка задачи.Количество комплектов мебели, перевозимых со станции в магазины
в магазины 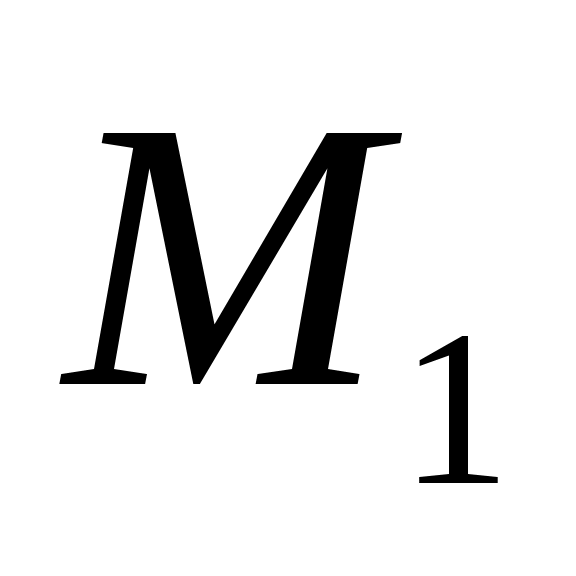 ,
, 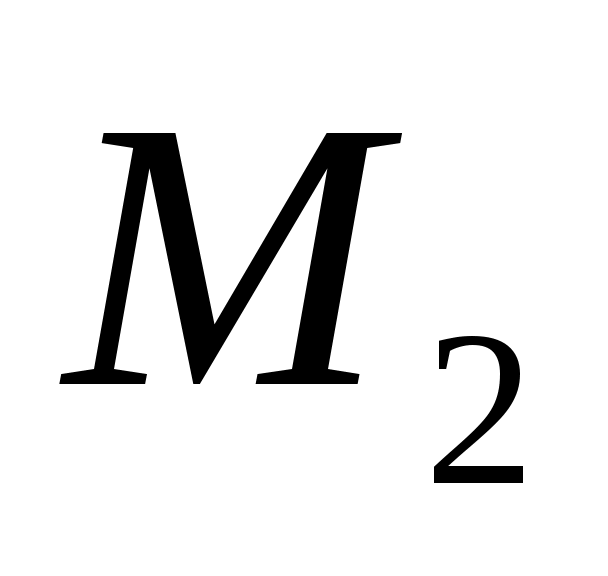 ,
, 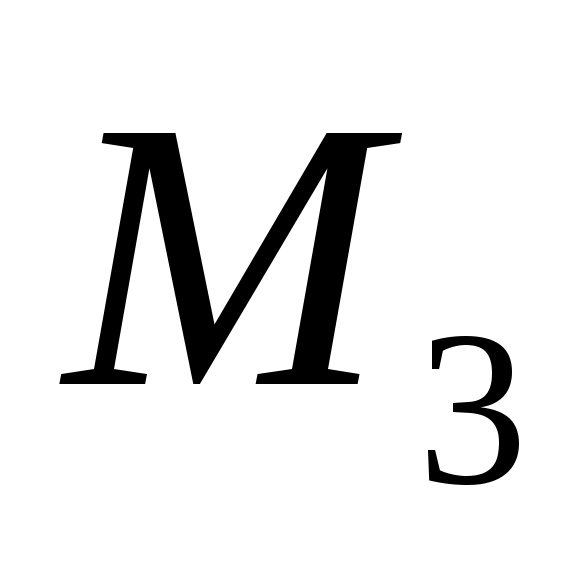 через
через  ,
,  ,
,  а со станции
а со станции  – через
– через 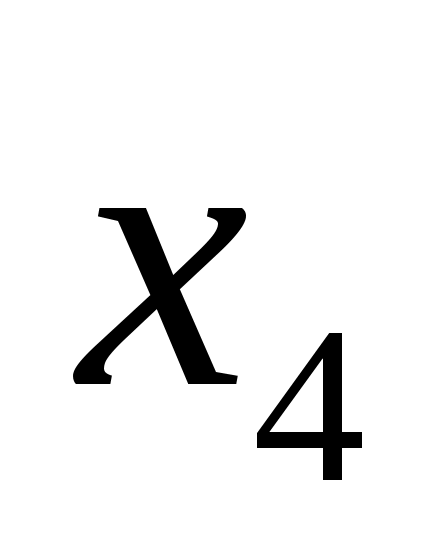 ,
, 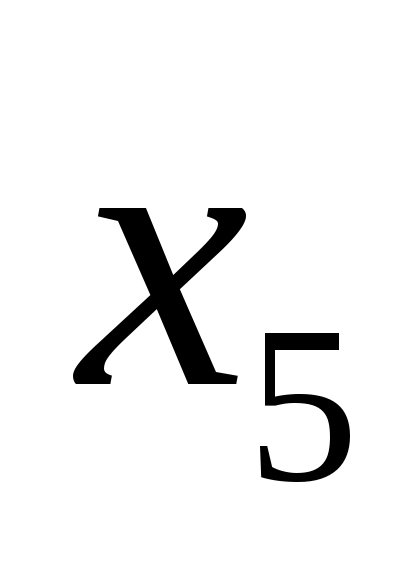 ,
, 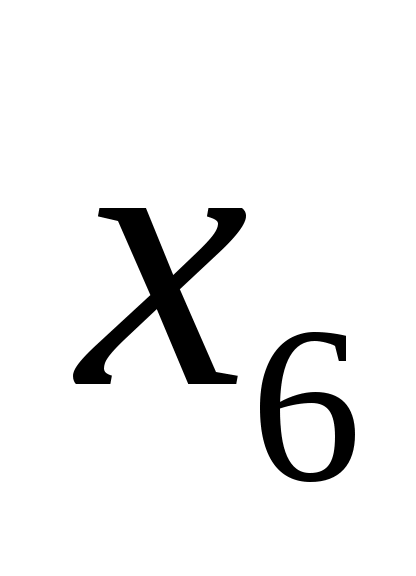 . Тогда схема перевозок буде выглядеть следующим образом:
. Тогда схема перевозок буде выглядеть следующим образом:
Таблица 2
В соответствии с условием задачи ( ,
, 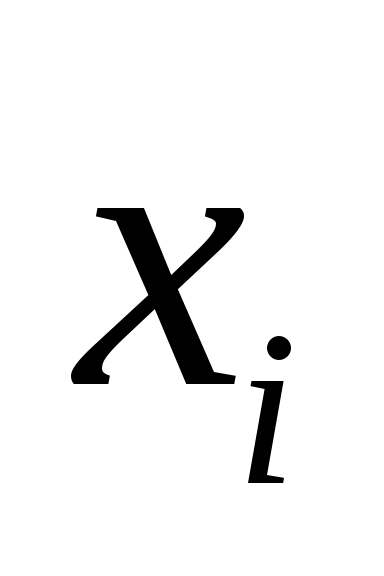 — целые,
— целые, 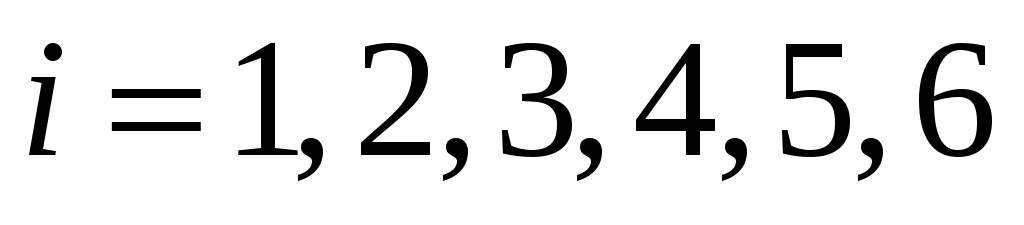 ). Задача сводится к тому, чтобы найти такое неотрицательное целочисленное решение системы (7)
). Задача сводится к тому, чтобы найти такое неотрицательное целочисленное решение системы (7)
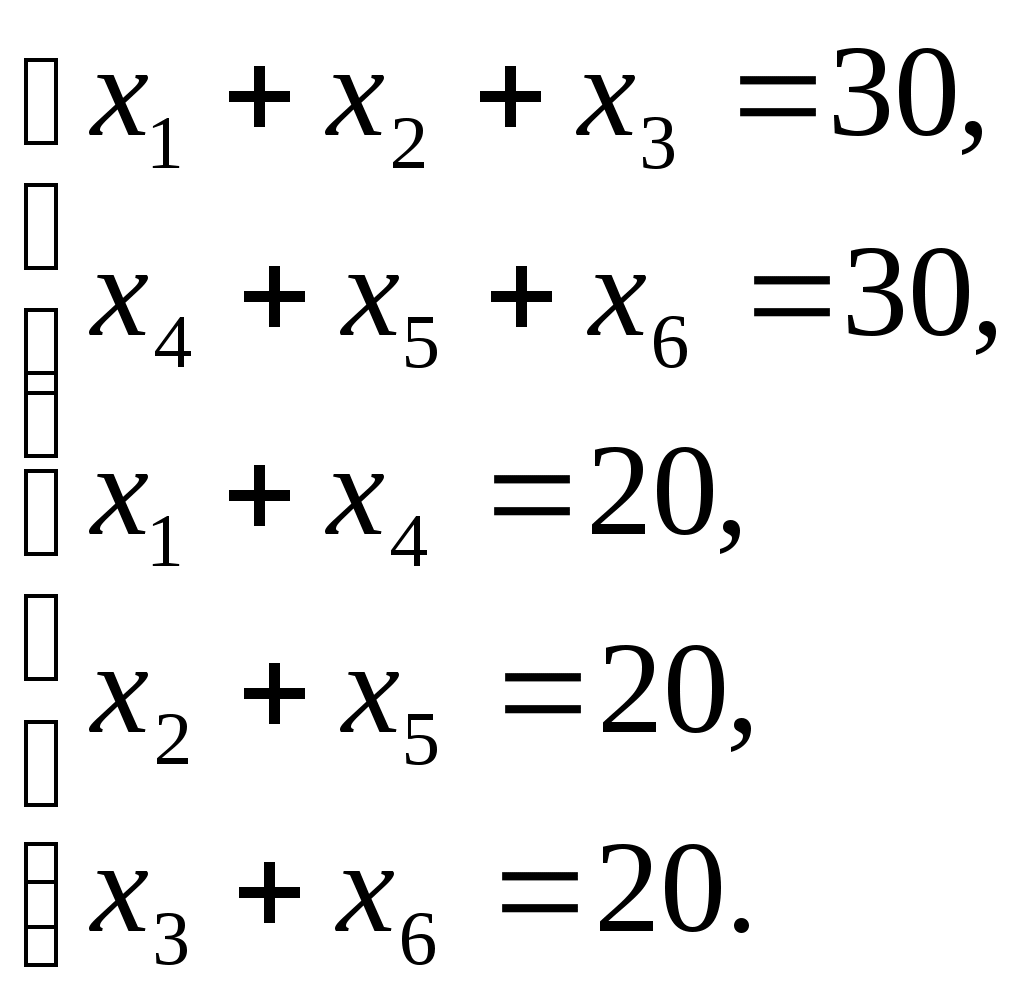 (7)
(7)
при котором линейная функция (стоимость перевозок)
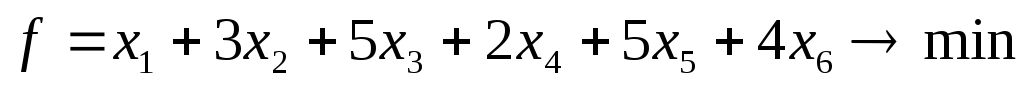 (8)
(8)
имеет наименьшее значение.
Решение задачи в MicrosoftExcelпредставлено на рисунке 11.
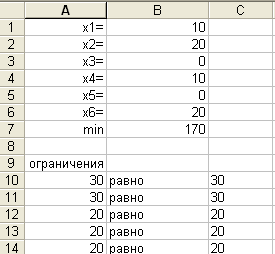
Рисунок 11 – Решение задачи
Решение задачи 3 в среде MathСad:
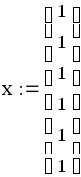
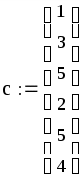
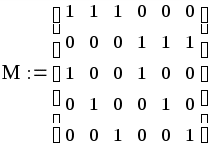
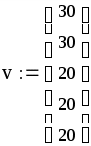

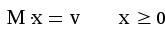
знак «жирное равно» выбирается на панели инструментов Логический или вставляется комбинацией клавиш Ctrl и =;

после чего получим оптимальный план
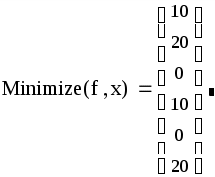
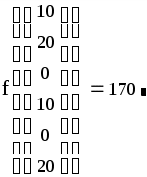
Полученные результаты совпали.
4.Задача производства

Рисунок 7 - Окно Добавление ограничения
Решение задачи 1 в среде MathСad:
-
запустить MathСad; -
задать начальное приближение:
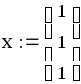
-
записать все коэффициенты из (3) и (4) в матричном виде:
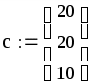
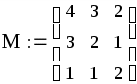
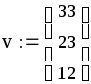
знак «присваивания» := находится на панели инструментов Вычисления; матрица (вектор) вставляется комбинацией клавиш Ctrl и M (англ.) или выбирается на панели инструментов Матрица, после чего вводятся количество строк и столбцов;
-
ввести целевую функцию (4) в виде:
знак «умножить» вставляется комбинацией клавиш Shift и *;
-
записать функцию Given; -
записать ограничения (3) в виде:
-
записать функцию минимизации
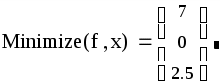
знак равенства вставляется с клавиатуры клавишей =;
после чего получим оптимальный план
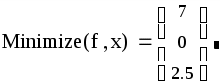
-
найти значение целевой функции в точке минимума:
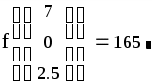
Таким образом, оптимальные планы Задачи 1 при решении в средах Microsoft Excel и MathСad получились различные (могут использоваться и те и другие), но целевая функция при этом имеет одинаковое значение.
Задача 2. В баре имеются три компонента: коньяк, шампанское, сок. Цель: подобрать оптимальный состав коктейля из этих трёх компонентов, если известно: стоимости ингредиентов в рублях:
Математическая постановка задачи 2. Пусть
Тогда должно быть:
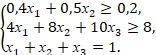 (5)
(5)(третье условие отражает наличие в составе смеси только трёх компонентов, т. е. то, что все три компонента составляют весь коктейль в целом — 1).
При этом линейная функция (стоимость коктейля) будет иметь вид:
Решение задачи 2 в Microsoft Excel имеет вид, представленный на рисунке 8 и 9.


Рисунок 8 – Окно с поиском решения Рисунок 9- Решение
Замечание 5. Для того, чтобы в решении задачи после запятой отображалось только 2 знака, надо выделить соответствующий диапазон ячеек, щёлкнуть на выделенном правой кнопкой мыши, в появившемся контекстном меню выбрать пункт Формат ячеек и на вкладке Число выбрать Числовой, указав Число десятичных знаков 2.
Решение задачи 2 в среде MathСad:
Получен оптимальный план
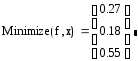
Для того чтобы MathСad отображал только 2 десятичных знака, надо выделить значения, для которых необходимо сменить формат вывода, в меню Формат выбрать подменю Результат — появится диалоговое окно Формат результата (рисунок 10) и указать количество десятичных знаков 2:

Рисунок 10 - Диалоговое окно Формат результата
Для вычисления значения целевой функции в точке минимума:
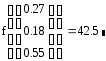
Таким образом, оптимальные планы Задачи 2 при решении в средах Microsoft Excel и MathСad получились одинаковые, а целевая функция при решении в среде MathСad имеет меньшее значение, таким образом, среда MathСad, в данном случае, даёт лучшее решение, чем Microsoft Excel.
3. Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
К группе задач о распределении ресурсов относят задачи, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время, затрачиваемое на неё и др., либо некоторая комбинация вышеперечисленного. В простейшем виде это задача о перевозках (транспортная задача).
Задача 3. На товарных станциях
в магазины
Математическая постановка задачи.Количество комплектов мебели, перевозимых со станции
Таблица 2
-
В
В
В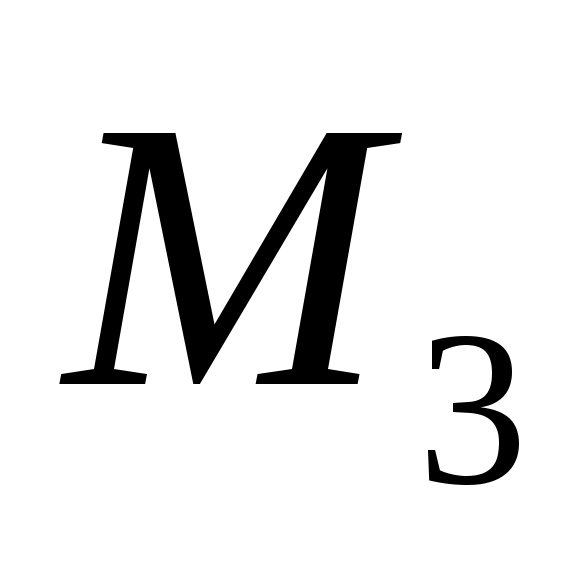
Всего
отправлено
Из



30
Из
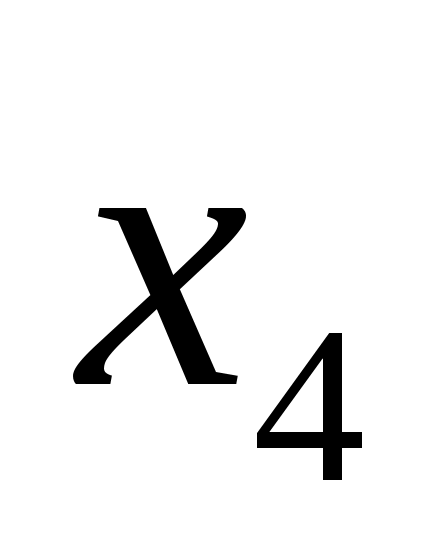
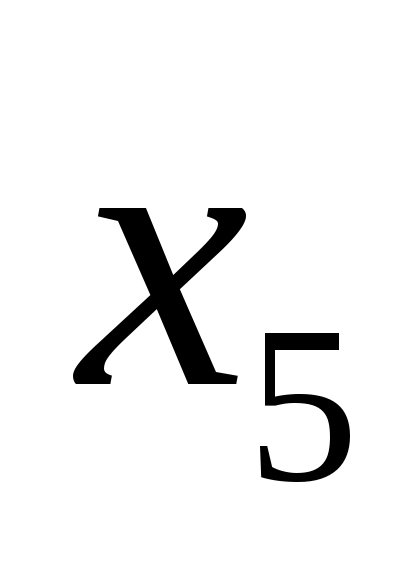
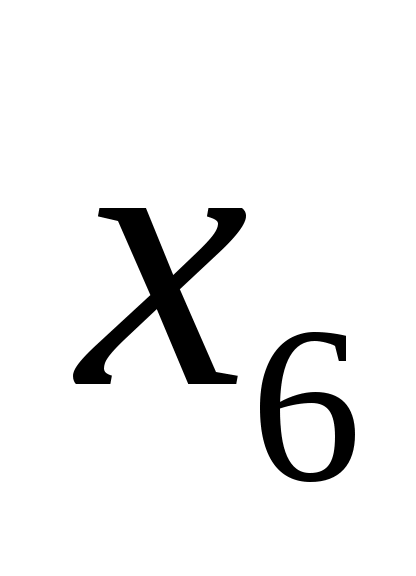
30
Всего получено
20
20
20
60
В соответствии с условием задачи (
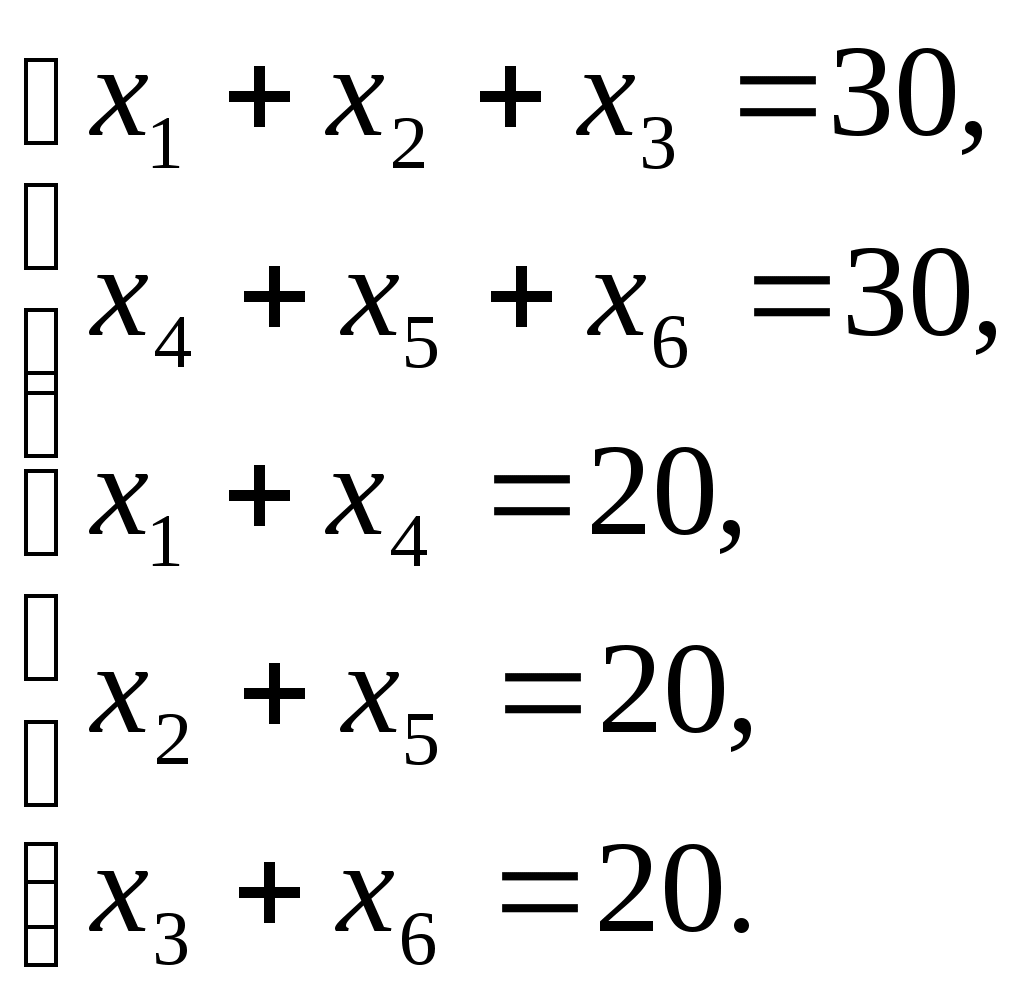 (7)
(7)при котором линейная функция (стоимость перевозок)
имеет наименьшее значение.
Решение задачи в MicrosoftExcelпредставлено на рисунке 11.

Рисунок 11 – Решение задачи
Решение задачи 3 в среде MathСad:
-
задать начальное приближение:
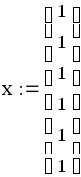
-
записать все коэффициенты из (1) и (2) в матричном виде:
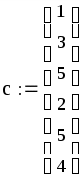
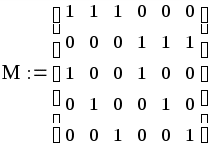
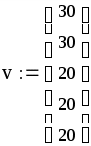
-
ввести целевую функцию (2) в виде:
-
записать функцию Given; -
записать ограничения (1) в виде:
знак «жирное равно» выбирается на панели инструментов Логический или вставляется комбинацией клавиш Ctrl и =;
-
записать функцию минимизации

после чего получим оптимальный план
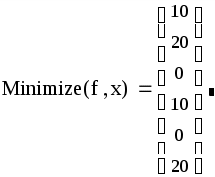
-
найти значение целевой функции в точке минимума:
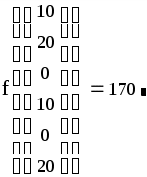
Полученные результаты совпали.
4.Задача производства