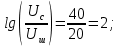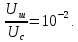САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА

_____________________________________________________________________________________

ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Контрольная работа

Дисциплина: Метрология и техническое регулирование

Фамилия: Пятаков

Имя: Сергей

Отчество: Игоревич

№ зачетной книжки: 1910462

Группа №: ПБ-92з

Проверил:

Санкт-Петербург

2022
СОДЕРЖАНИЕ

1. Задание 1. ……..………………………….…………………..…………...	3
2. Задание 2. ……..………………………….……………………………….	4
3. Задание 3. ………………………..……….…………………..…………..	7
4. Задание 4. ………………………..……….…………………..…………..	9
5. Задание 5. ………………………..……….…………………..…………..	11
6. Список использованных источников ……………………………………	12

Задание 1.

Случайная погрешность прибора для измерения сопротивления изоляции имеет три независимые составляющие, средние квадратические значения которых равны 0,6 МОм, 0,2 МОм и 1,5 МОм соответственно. Определите значение результирующей средней квадратической погрешности прибора и доверительный интервал для однократного измерения сопротивления изоляции при доверительной вероятности 0,95. Сколько наблюдений надо сделать, чтобы в три раза уменьшить погрешность измерения среднего значения сопротивления изоляции? Закон распределения случайной погрешности прибора принять нормальным.
Решение:
Рассчитываем значение средней квадратической погрешности прибора по формуле:



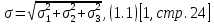
где , ,

---

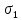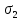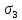
– заданные СКО составляющих случайной погрешности прибора.



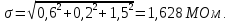
В предположении нормальном законе распределения случайной погрешности для определения доверительного интервала для однократного измерения сопротивления изоляции справедлива запись:



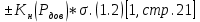
При заданной доверительной вероятности 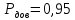соответствующее значение коэффициента 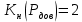. Следовательно, искомый доверительный интервал может быть представлен в виде: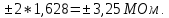



Известно, что если за результат измерения взять среднее арифметическое из 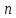измерений, то точность повышается в 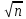раз.

Таким образом, чтобы в три раза уменьшить погрешность измерения среднего значения сопротивления изоляции (а это означает, что 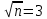), необходимо сделать: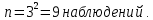



Задание 2.

Электронным вольтметром постоянного напряжения, нормируемая относительная погрешность которого находится в пределах ± 2,0 %, измеряют сигнал, форма которого показана на рис. 2.1.



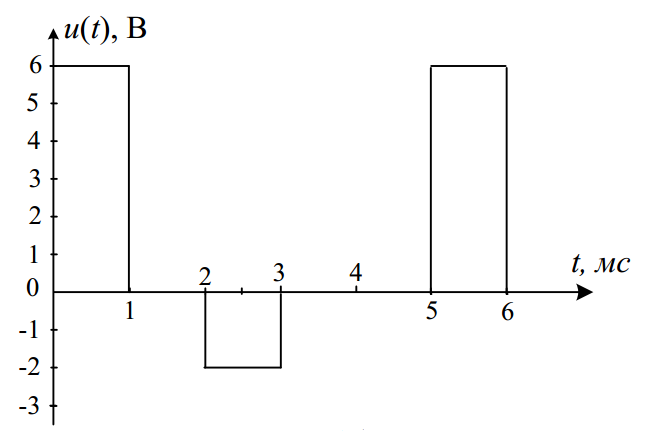
Рисунок 2.1
Запишите результат измерения постоянной составляющей этого сигнала с оценкой абсолютной погрешности.

Изобразите на графике, как изменится этот сигнал при прохождении через RC – цепочку закрытого входа. Определите показания электронного вольтметра переменного напряжения с закрытым входом и выпрямительным преобразователем при измерении такого сигнала. Предел измерения этого вольтметра 2,5 В, а нормируемая относительная погрешность ± 1,5%.
Решение:

Вольтметр постоянного напряжения оперирует постоянной составляющей измеряемого напряжения. Поэтому его показания равны среднему значению 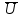исследуемого напряжения за период.

Рассматриваемый сигнал прямоугольной формы имеет период

---

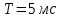
и характеризуется тем, что на части периода он равен какому-то постоянному значению, а на оставшейся части периода он равен нулю.

Математическая модель данного сигнала имеет вид:



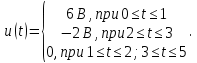
В соответствии с этим и определяем искомое среднее значение напряжения за период по формуле:



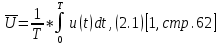
где – среднее значение напряжения за период; 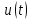– мгновенное значение измеряемого сигнала; 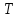– период синала.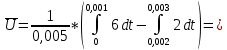





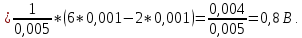
По условию задачи для вольтметра постоянного напряжения известна его относительная погрешность .

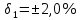Тогда предельно допускаемая абсолютная погрешность будет равна:




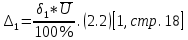
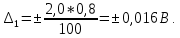
Записываем результат измерения:



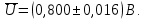
При прохождении через RC – цепочку закрытого входа исходный сигнал будет выглядеть следующим образом:

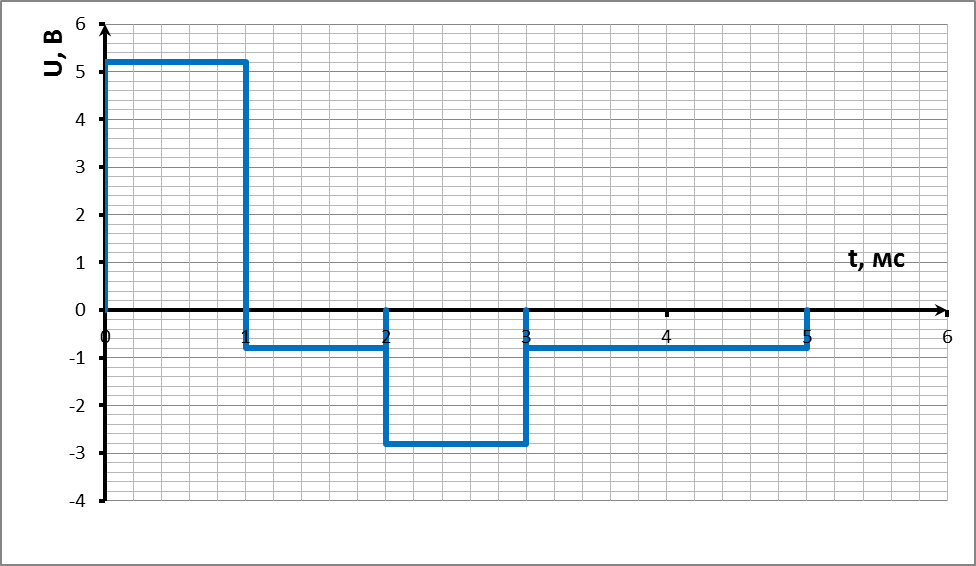
Показания вольтметров с открытым (ОВ) и закрытым входом (ЗВ) различаются тем, что вольтметр с закрытым входом отсекает постоянную составляющую сигнала. Кроме того, наличие выпрямительного преобразователя позволяет заключить, что вольтметр переменного напряжения в данном случае будет измерять средневыпрямленное значение переменной составляющей.

Таким образом, средневыпрямленное значение измеряемого напряжения:





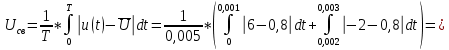
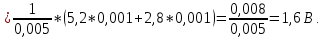
Для показаний вольтметра переменного напряжения



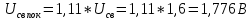
задан предел измерения 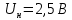и нормируемая относительная погрешность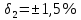

---

.

Тогда предельно допускаемая абсолютная погрешность будет равна:



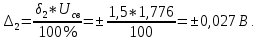
Записываем результат измерения:



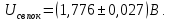
Задание 3.

На входы X и Y осциллографа поданы внешние развертывающие сигналы, форма которых показана на рис. 3.1. Постройте изображение, которое получится на экране осциллографа.





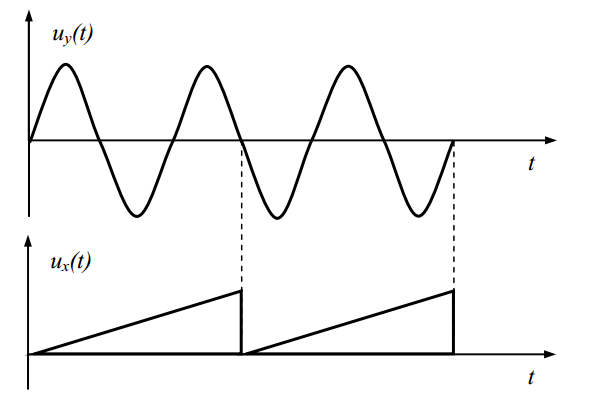
Рисунок 3.1
Решение:
Исследуемый луч подается к вертикально отклоняющим пластинам и вызывает смещение луча по вертикали. Для получения изображения необходимо, чтобы луч одновременно перемещался с постоянной скоростью и по горизонтали (такое смещение луча обеспечивает напряжение развертки). Таким образом, для каждого выбранного момента времени мы определяем точку, соответствующую определенному смещению луча и по вертикали, и по горизонтали. По мере нарастания или убывания пилообразного напряжения развертки луч отклоняется, светящаяся точка на экране перемещается по горизонтальной оси от начала до конца экрана. В момент спада пилообразного напряжения до нуля луч (светящаяся точка) почти мгновенно возвращается в исходное положение. Обратный ход луча полезной информации не несет, поэтому его линия на осциллограмме занимает очень малое время (из-за инертности глаз и экрана мы его не видим).

В начальный период времени пятно на экране находится в точке 0 координатной сетки. В момент времени 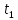луч смещается по вертикали на 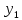, а по горизонтали – на 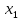, что соответствует положению пятна на экране в точке 1. Затем в момент времени 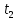луч смещается по вертикали на 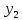, а по горизонтали – на 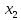, что соответствует положению пятна на экране в точке 2 и так далее.

В точке 12 будет иметь место обратный ход луча по экрану осциллографа (падения напряжения развертки до нуля).

В течение последующих периодов луч и пятно на экране будут повторять свое движение.

---

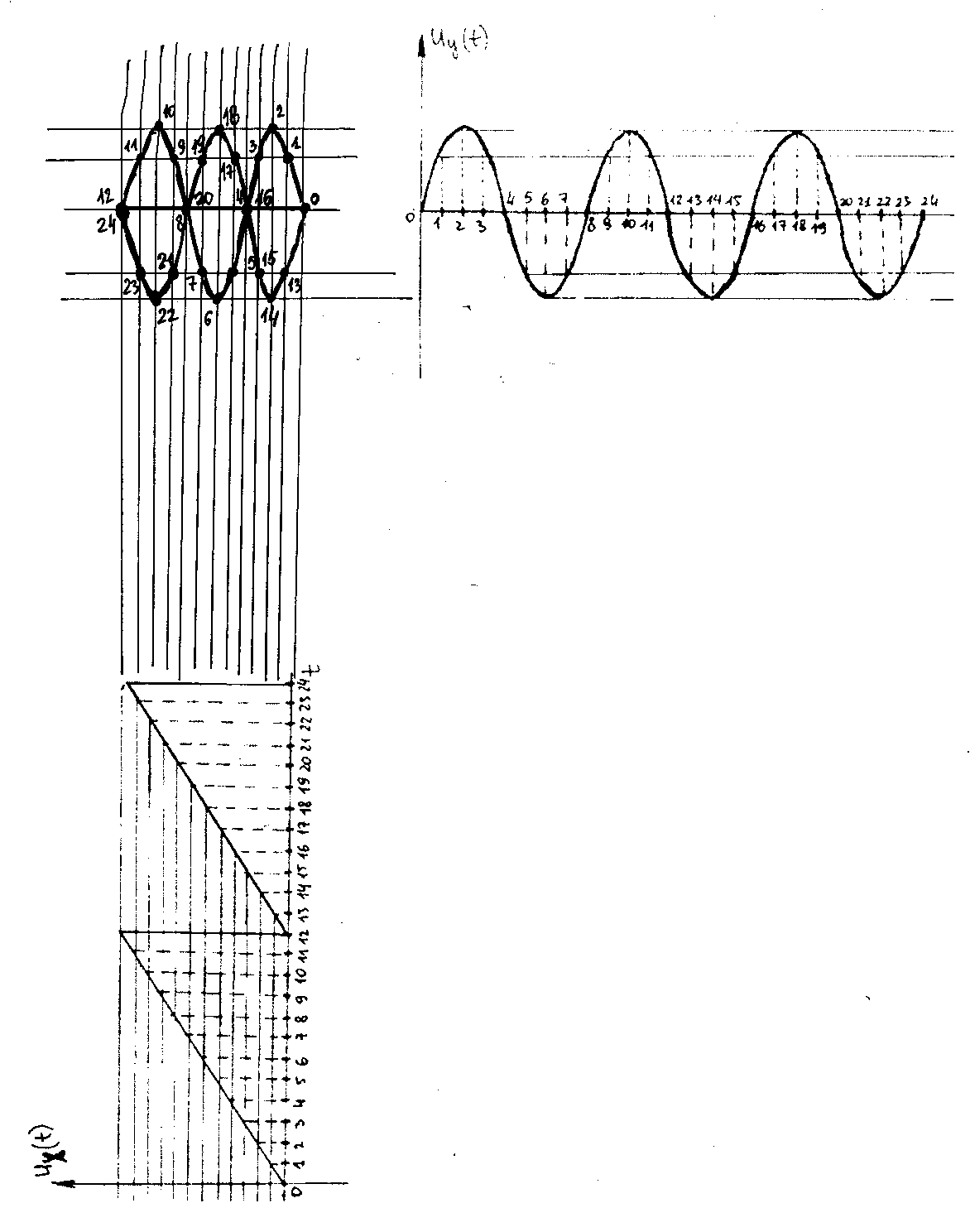
Рисунок 3.2

Задание 4.

Оцените, с какой абсолютной погрешностью можно измерить период напряжения питающей сети, если отношение сигнал-шум в измеряемом сигнале 40 дБ. В распоряжении имеется цифровой частотомер со следующими характеристиками: относительная погрешность опорного кварцевого генератора находится в пределах ±5·10^–6; частота меток времени, формируемых из сигнала опорного генератора, может быть установлена равной 0,1; 1 или 10 МГц. Напишите формулу для суммарной абсолютной погрешности измерения периода, назовите составляющие суммарной погрешности, выберите частоту меток времени, оцените абсолютную погрешность измерения периода частоты сети, запишите в соответствии с правилами возможный результат измерения.
Решение:
Результирующая (суммарная) предельная относительная погрешность измерения периода 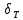определяется тремя составляющими: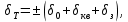



где – предельная погрешность опорного генератора; 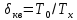– предельная погрешность квантования (дискретности); 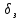– погрешность уровня запуска.

Погрешность уровня запуска в свою очередь складывается из нескольких составляющих: погрешности срабатывания формирующих устройств прибора, погрешности вследствие наличия шумов в измеряемом сигнале и т.п. При измерении периода синусоидального с амплитудой U_c при наличии шума с пиковым значением U_ш максимальная относительная погрешность уровня запуска может быть оценена по формуле:



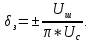
Объединим все перечисленные составляющие погрешности в одну формулу:



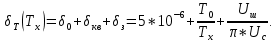
Выразим отношение напряжения сигнала к напряжению шума из величины :

---

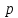Смотрите также файлы

• Практическая работа моу сош с. Кикино Девликамов Н. Р. Управление кадровым потенциалом Практическая работа 3 (Часть 3).pdf

• Бекітемін Кні 13. 04. 2021 ж.doc

• Основные требования законодательства Российской Федерации о труде и охране труда.docx

• Структура правоотношений в сфере образования.rtf

• Цинская эффективность.doc