Файл: Министерств.docx

Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:90х₁+140х₂Используя обозначения соответствующих ячеек в Excel, получим следующее:=СУММПРОИЗВ(B10:C10;B7:C7)Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, C10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, C7).Таким образом, для первого ограничения в ячейку В14 будет введена формула:=СУММПРОИЗВ($B$10:$C$10;B3:C3),где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. 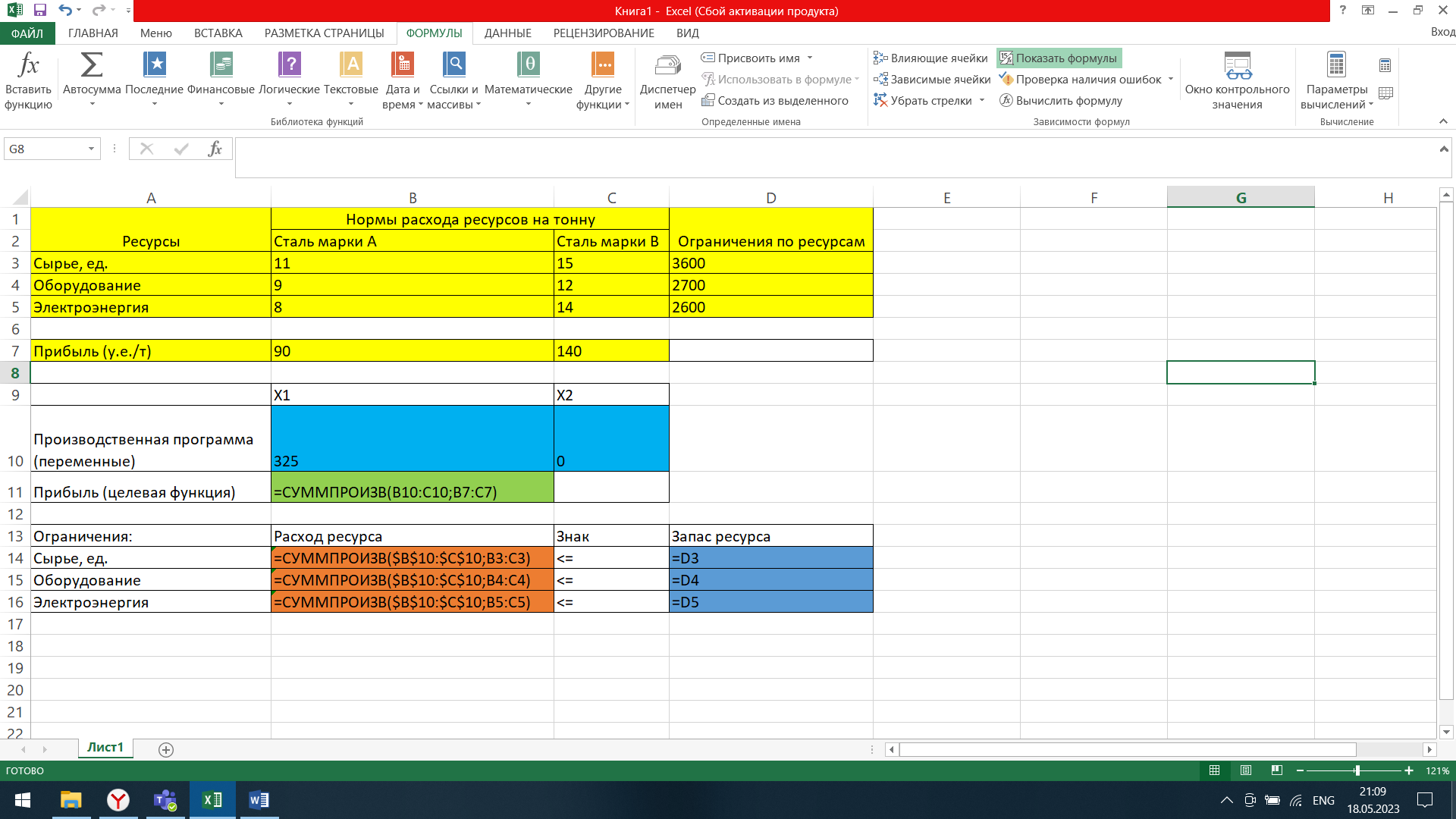Этот номер является строкой, где записано ограничение.Рис.1.3. (Ячейки с заполненными формами)С помощью надстройки «Поиск решения» найдем решение данной задачи. 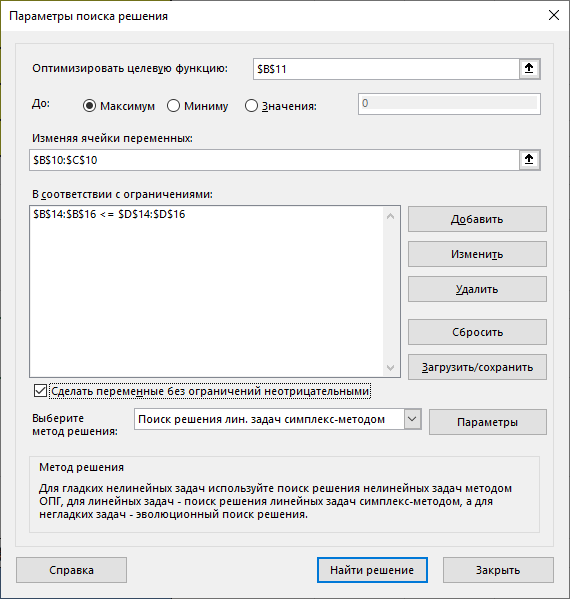В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.Рис.1.4. На данном этапе вводится задача параметров для поиска решений с помощью надстройки.Рис.1.5. 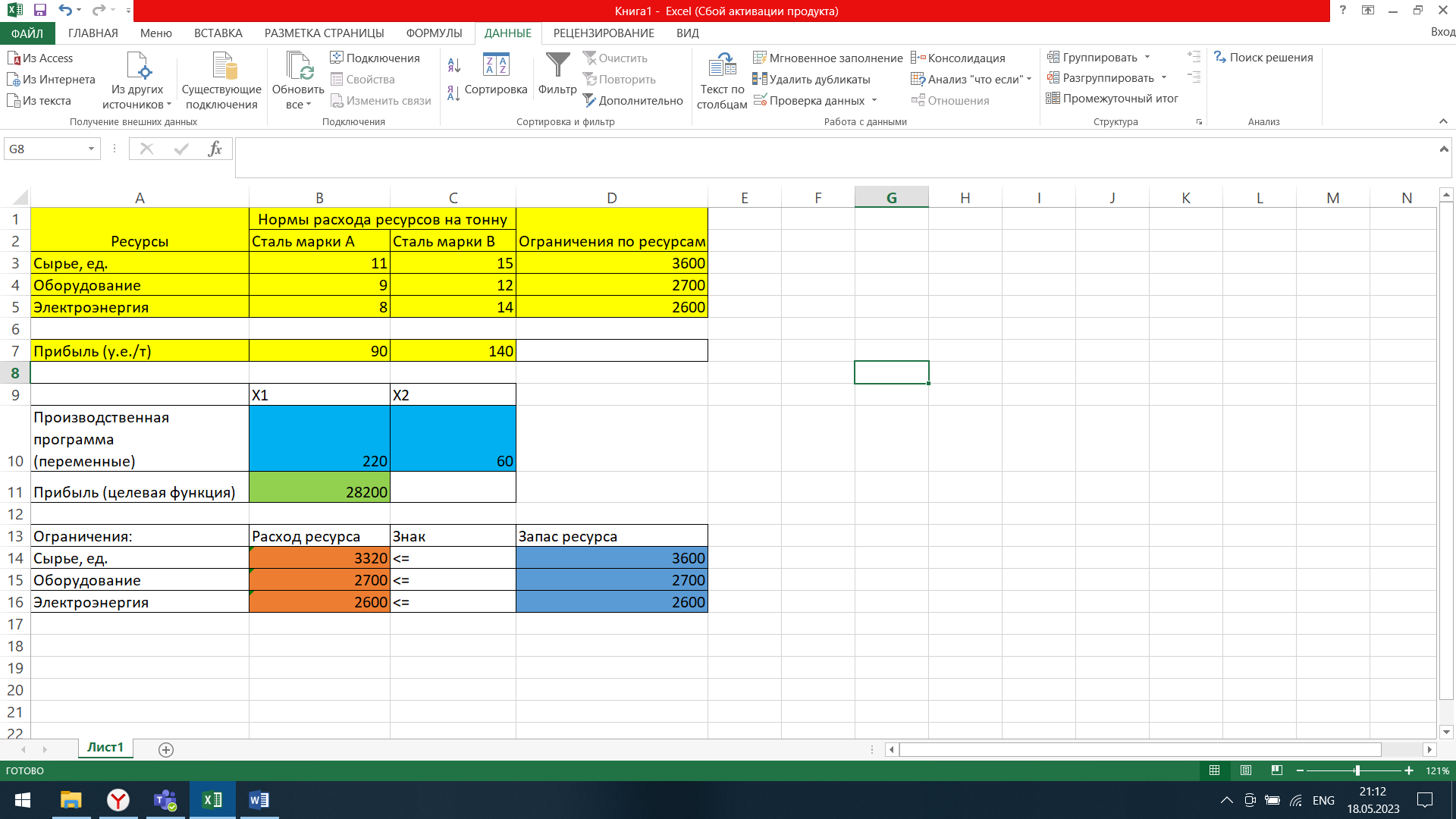Далее, после нажатия кнопки с предыдущего скриншота «Найти решение», видно уведомление о нахождении решенияРис.1.6. (Результат поиска решений)4. Интерпретация результатов и общий вывод При решение графическим методом и при решении с помощью надстройки «Поиск решения» получилась одинаковая максимальная прибыль. Следовательно, оба метода подходят для решения данной задачи. Также хочется отметить, что производственная программа обеспечит максимальную прибыль, равную 28200, при выпуске объема стали марки А в количестве 220 тонн и стали марки В в количестве 60 тонн, а также при расходе ресурсов таким образом: сырье – 3300 ед, оборудование 2700 ед, электроэнергия 2600 ед. Кейс-задание №2BПредприятие может выпускать три марки стали: сталь марки А, сталь марки B и сталь марки C. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.

---

Ресурсы	Нормы расхода ресурсов на тонну продукции			Ограничения по ресурсам
	Сталь марки A	Сталь марки B	Сталь марки C
Сырье, ед.	0,55k	0,75k	1,1k		3200+20k
Оборудование, ед.	0,45k	0,6k	k		2100+30k
Электроэнергия, ед.	0,4k	0,7k	0,9k		2100+25k
Прибыль (у.е./т)	90	140	200

Таблица 2.1. Таблица с исходными данными.Недельные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены финансовыми средствами, емкостью складских помещений, логистическими ограничениями и т.д., по оборудованию – плавильными мощностями и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице 4.

Ресурсы	Нормы расхода ресурсов на тонну продукции				Ограничения по ресурсам
	Сталь марки A	Сталь марки B	Сталь марки C
Сырье, ед.	11	15	22	3600
Оборудование, ед.	9	12	20	2700
Электроэнергия, ед.	8	14	18	2600
Прибыль (у.е./т)	90	140	200

Таблица 2.2. Таблица со значениями варианта. Требуется сформировать недельную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной.

---

Для этого предлагается:

1. 
   Составить математическую модель данной задачи
   
2. 
   Решить задачу линейного программирования симплекс-методом;
   
3. 
   Решить задачу линейного программирования с использованием
   

надстройки «Поиск решения» MS Excel;

4. 
   Провести интерпретацию результатов и сделать выводы;
   
5. 
   Исследовать оптимальное решение по следующей схеме (ответы
   

обосновать с помощью результатов «Поиска решения»):А). Определить дефицитные и избыточные ресурсы;Б). Насколько можно уменьшить запасы избыточных ресурсов, чтобы программа производства не пострадала?В). Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5%;Г). Как изменится производственная программа при уменьшении прибыли, получаемой от стали марки А, на N единиц, где N – число букв в фамилии студента, выполняющего курсовую работу. 1. Математическая модель данной задачи 1) критерий – максимум прибыли 2) переменные:x₁ – количество стали марки Аx₂ – количество стали марки Вx₃ – количество стали марки С3) целевая функция – максимизация прибыли. Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб, гаек и болтов. Таким образом, суммарная прибыль, то есть целевая функция:Z(X) = 90х₁+140х₂+200х₃  max4) система ограничений: Ограничения по запасам ресурса на три вида продукции.Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х₁, х₂, х₃. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения: 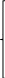- по сырью:11х₁ + 15х₂+22х₃ ≤ 3600;- по оборудованию:9х₁ + 12х₂ +20х₃ ≤ 2700;- по электроэнергии:8х₁ + 14х₂ +18х₃ ≤ 26002. 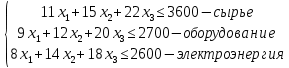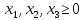Решение задачи линейного программирования симплексе-методом Z(X) = 90х₁+140х₂+200х₃  max1) Приведем задачу линейного программирования к каноническому виду:

---

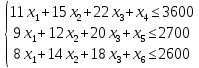
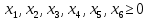
-Z(x)= -90 x₁ -140 x₂ - 200 x₃ -> minПеременные 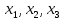– свободные; 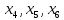- базисные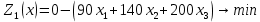Данному базисному решению соответствует следующая симлпекс-таблица

	Своб. член	х1	х2	х3
Z1	0	90	140	200
х4	3600	11	15	22
х5	2700	9	12	20
х6	2600	8	14	18

Таблица 2.3. Симплекс-таблица.Нашли генеральный элемент – 20, т.к. в строке Z выбираем положительное число (у нас число 200 – выбираем столбец х3) а в столбце х₃, не считая строки Z, выбираем то значение, для которого отношение к нему свободного члена минимально (2700/20 – минимальное значение). В новом допустимом базисном решении х₃ и х₅ изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:

	Своб. Член	х1	Х2	Х5
Z1	-27000	0	-20	10
х4	630	11/10	9/5	-11/10
Х3	135	9/20	3/5	1/20
Х6	170	-1/10	16/5	-9/10

---

Таблица 2.4. Решение симплекс-методом.Определяем генеральный элемент в новой таблице – 16/5. В новом допустимом базисном решении х₂ и х₆ изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:

	Своб. член	х1	Х6	Х5
Z1	-56125/2	-5/8	25/4	25/8
х4	17100/37	37/32	-9/16	-19/32
Х3	220	15/32	-3/16	-9/32
Х2	0	-1/32	-5/16	35/8

Таблица 2.5. Решение симплекс-методом.В этой таблице определяем новый генеральный элемент – 15/32 и строим новую таблицу, меняя местами х₁ их₃:

	Своб. член	Х3	Х6	Х5
Z1	-28200	4/3	6	14/3
х4	280	-37/15	-1/10	-17/15
Х1	220	32/15	-2/5	7/15
Х2	60	1/15	3/10	-4/15

Таблица 2.6. Конечный вид симплекс-таблицы.Далее генеральный столбец выбрать нельзя. Значит, оптимальное решение имеет вид:

---