ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 424
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Хопт= (220; 60; 0)Zmin=-28200, следовательно Zmax= 28200Zmax=90*220 +140*60 +200*0= 28200Вывод: при объеме выпуска 220 тонн стали марки A, 60 тонн стали марки B и 0 тонн стали марки C максимальная прибыль от реализации составит 28200 у.е.3. Решение задачи линейного программирования с помощью надстройки «Поиск решения» MS ExcelПостроив математическую модель, можно перейти к построению табличной модели. 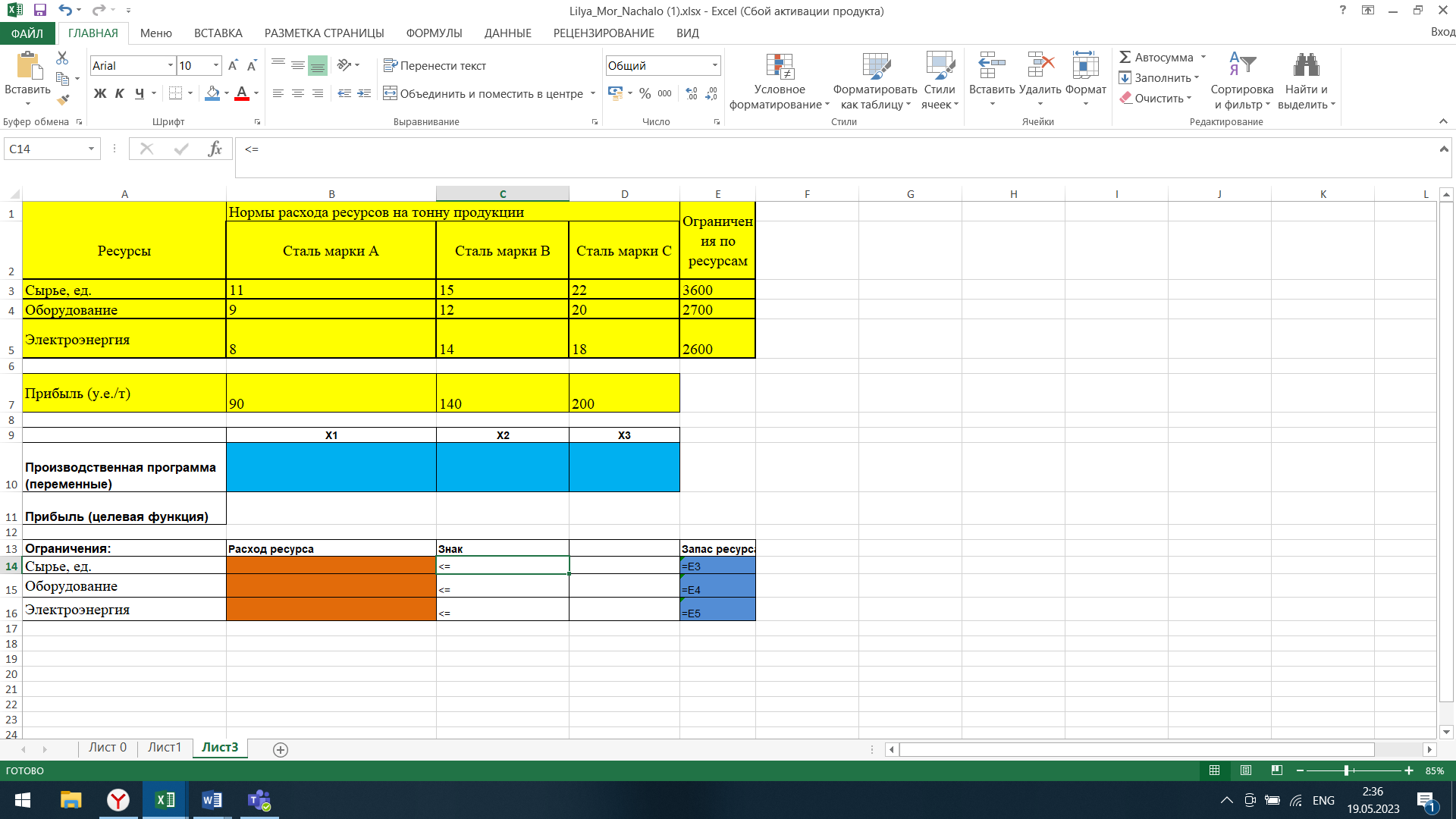Для этого введем данные – параметры, которые характеризуют выпуск стали, в единую таблицу.Рис. 2.1. Таблица с данными.В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:90х1+140х2+200х3Используя обозначения соответствующих ячеек в Excel, получим следующее:=СУММПРОИЗВ(B10:D10;B7:D7)Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, D10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, D7).Таким образом, для первого ограничения в ячейку В14 будет введена формула:=СУММПРОИЗВ($B$10:$D$10;B3:D3),где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. 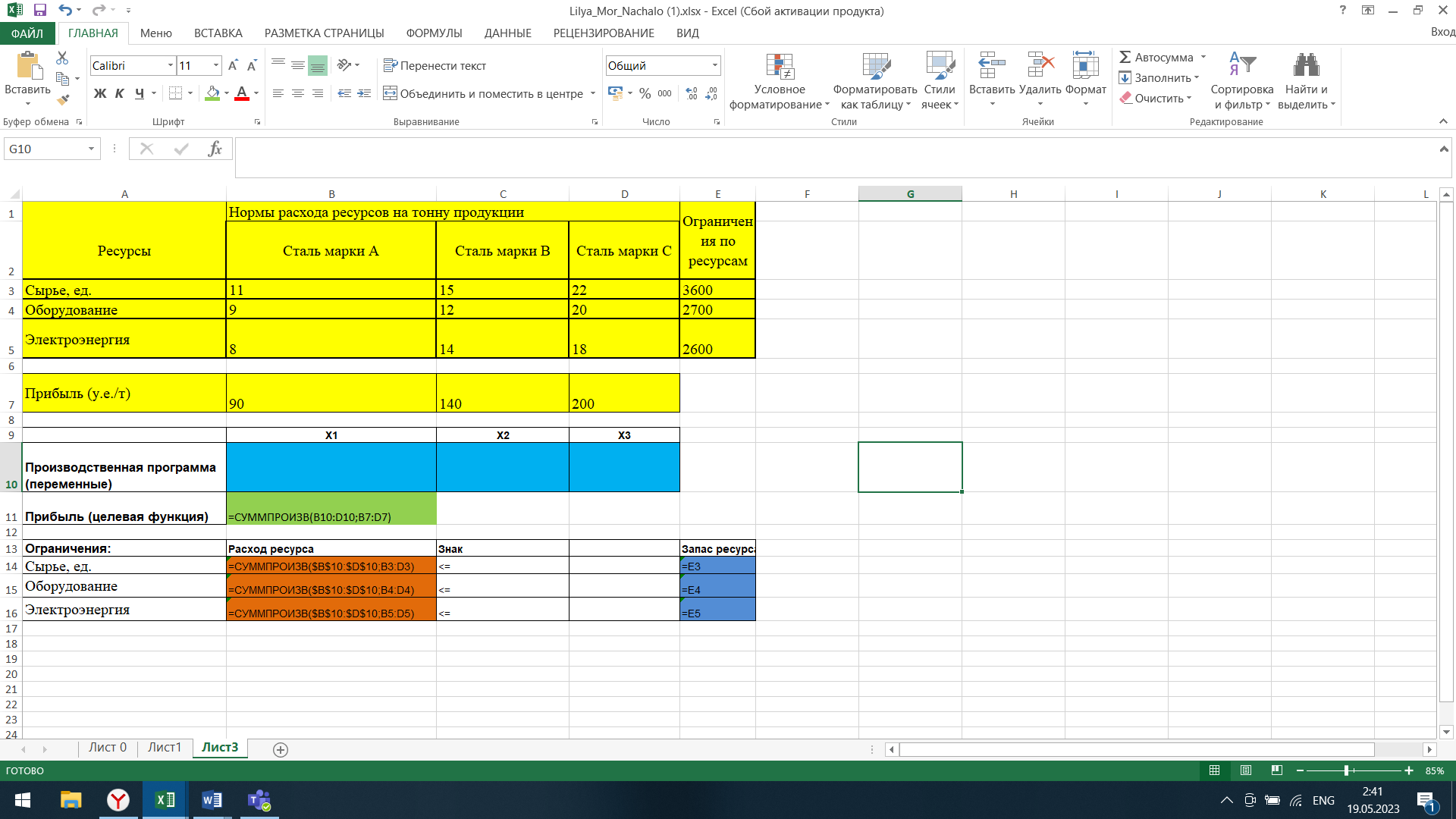Рис. 2.2. Таблица с формулами.С помощью «Поиска решения» найдем решение данной задачи. 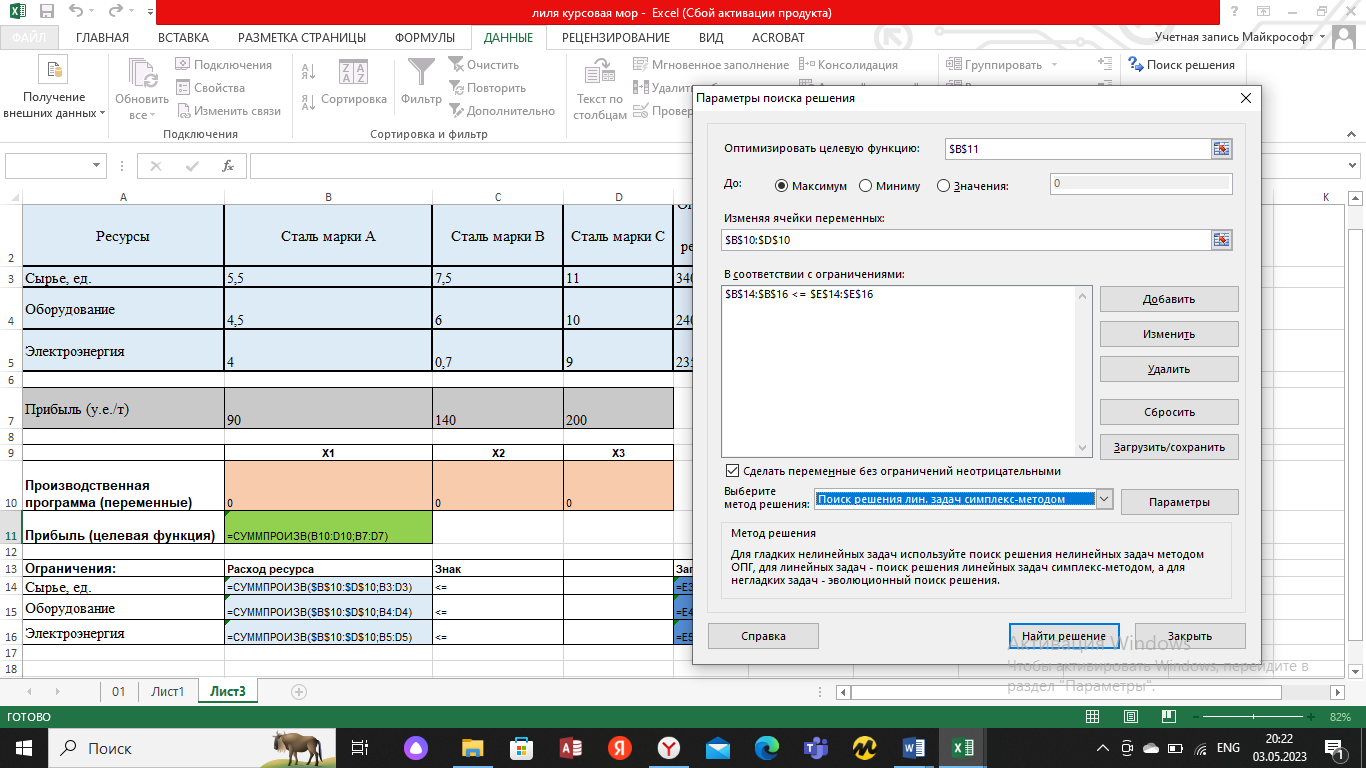В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.Рис. 2.3. 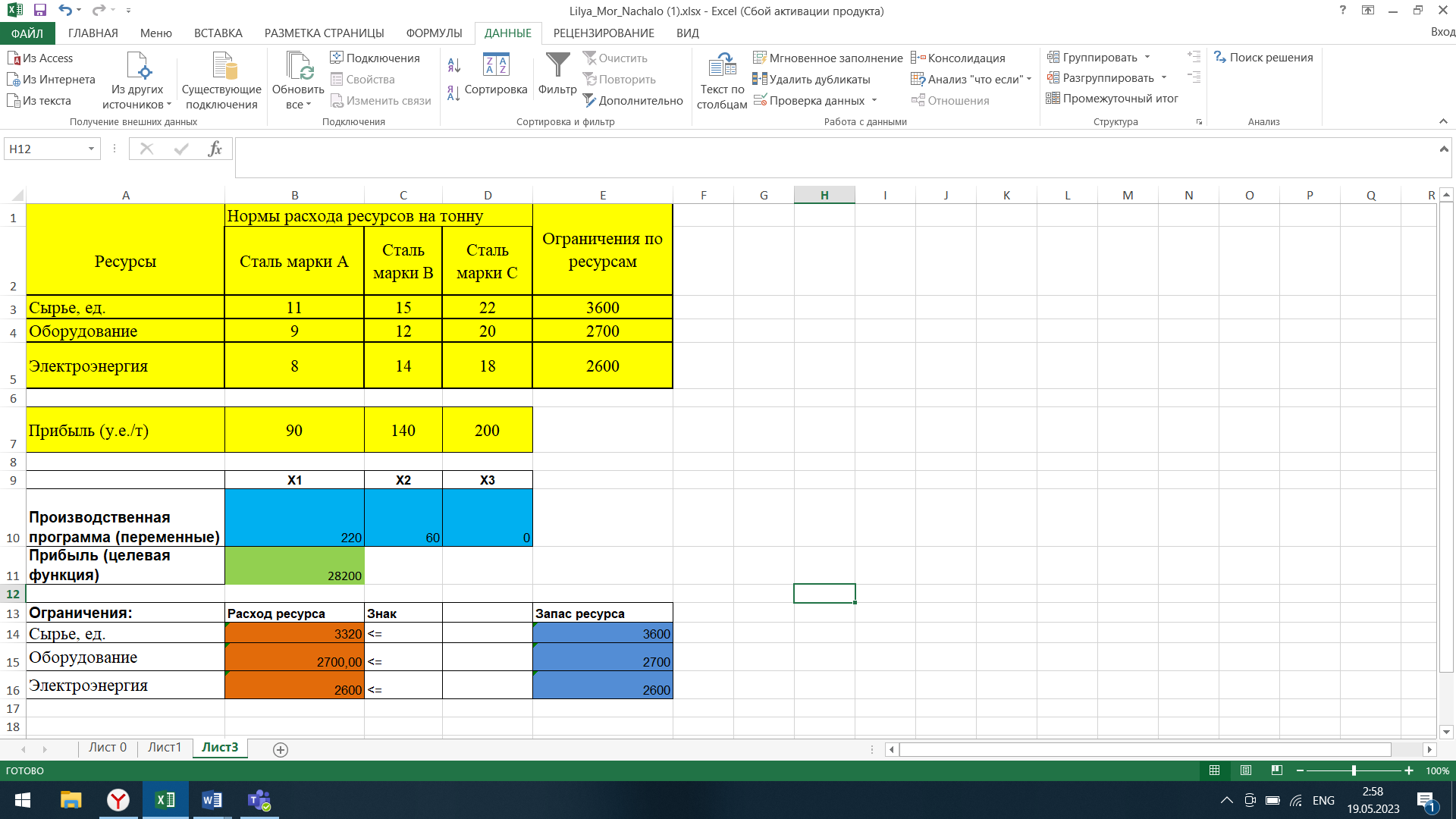Параметры поиска решений.Рис. 2.4. Таблица с конечным результатом.Вывод: В результате решения Кейса №2 симплекс-методом и надстройкой «Поиск решения» в MS Excel получилось, что при объеме выпуска 220 тонн стали марки A, 60 тонн стали марки B и 130 тонн стали марки C максимальная прибыль от реализации составит 28200 у.е.5. Исследование оптимального решения:А) Исходя из данных, можно понять, что
дефицитные ресурсы –оборудование и электроэнергия; избыточные ресурсы – сырье.Б) Избыточным является сырьё. Для того, чтобы выяснить, сколько нужно уменьшить, вычтем из 3600 разность числа 3600 и 3320 – 280. Теперь получим оптимальный результат, при котором производство не пострадает.Рис. 2.5. Уменьшение избытка.В) Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5%.К дефицитным запасам у нас относится оборудование и электроэнергия, значит, увеличим их на 5%. То есть, к электрооборудованию 2700 прибавим 135, а к электроэнергии 2600 прибавим 130. Получим следующие результаты:Рис. 2.6. Таблица с увеличением запасов.Г) При уменьшении прибыли стали марки А на 9 (Сальников) и поиску оптимального решения, произойдёт изменение производственной программы. Результаты будут следующие:Рис. 2.7. Таблица с уменьшением прибыли.По новой производственной программе будет производиться 0т. стали марки А, 58,59т. стали марки В и 106,09т. стали марки С, но, с последующим небольшим увеличением прибыли на – 29421,875 вместо 28200, что, несомненно, является положительным моментом.
В данной курсовой работе была рассмотрена и решена задача линейного программирования. Для решения был применён метод линейного программирования, а именно: графический метод и надстройка «Поиск решения» в Microsoft Excel.В данной курсовой работе были рассмотрены и решены основные задачи линейного программирования: задачи оптимизации производства, задача составления смеси и составления расписания. Для решения данных задач были применены методы линейного программирования, а именно: графический метод и симплекс-метод, а также использовалась надстройка Microsoft Excel «Поиск решения».В результате выполнения работы были сформированы математические модели задач, были получены решения с помощью графического метода, симплекс-метода и надстройки «Поиск решений» в MSExcel, а также проведён анализ полученных данных.
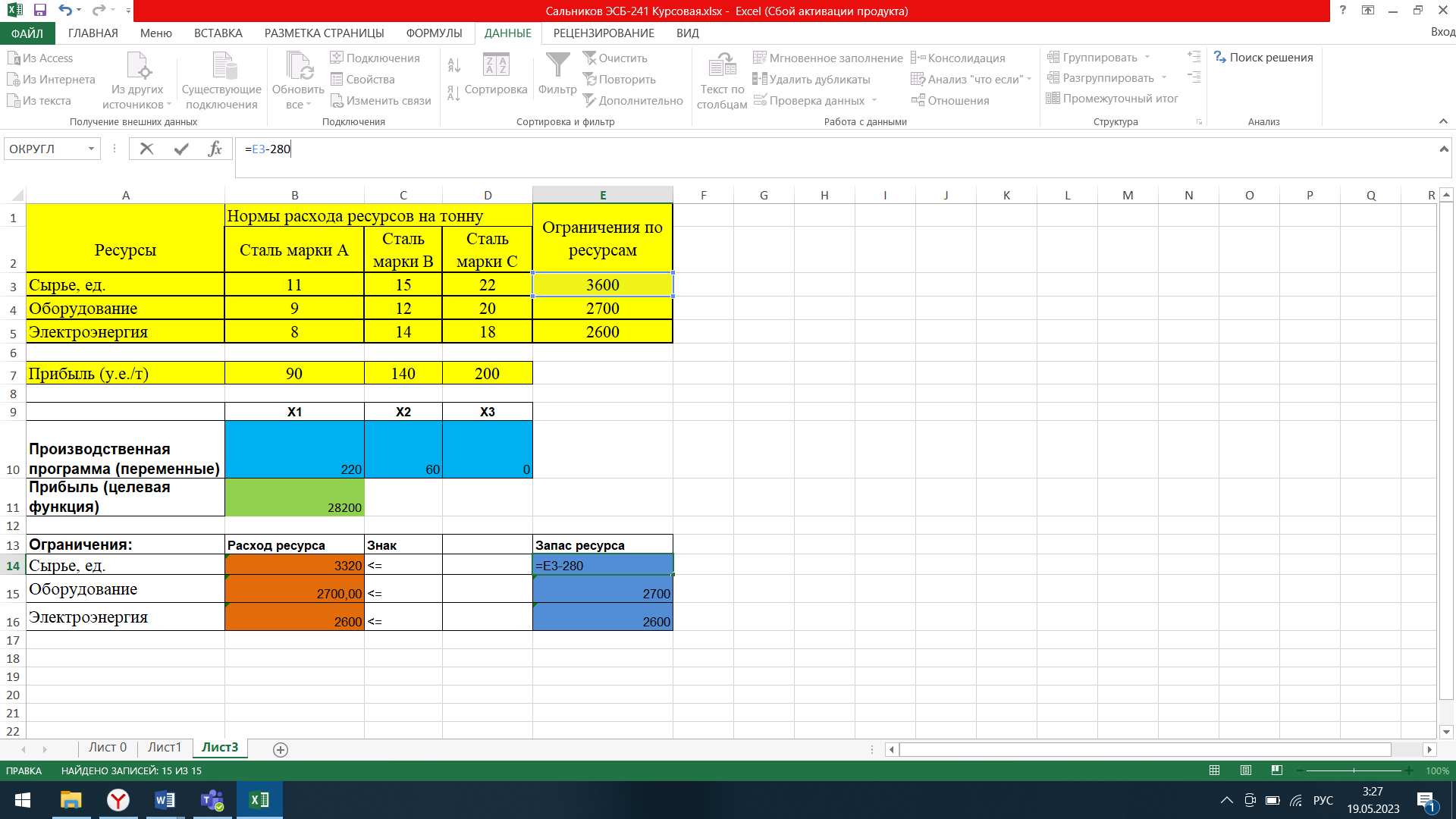
дефицитные ресурсы –оборудование и электроэнергия; избыточные ресурсы – сырье.Б) Избыточным является сырьё. Для того, чтобы выяснить, сколько нужно уменьшить, вычтем из 3600 разность числа 3600 и 3320 – 280. Теперь получим оптимальный результат, при котором производство не пострадает.Рис. 2.5. Уменьшение избытка.В) Как изменится производственная программа и прогнозируемая прибыль при увеличении запасов дефицитных ресурсов на 5%.К дефицитным запасам у нас относится оборудование и электроэнергия, значит, увеличим их на 5%. То есть, к электрооборудованию 2700 прибавим 135, а к электроэнергии 2600 прибавим 130. 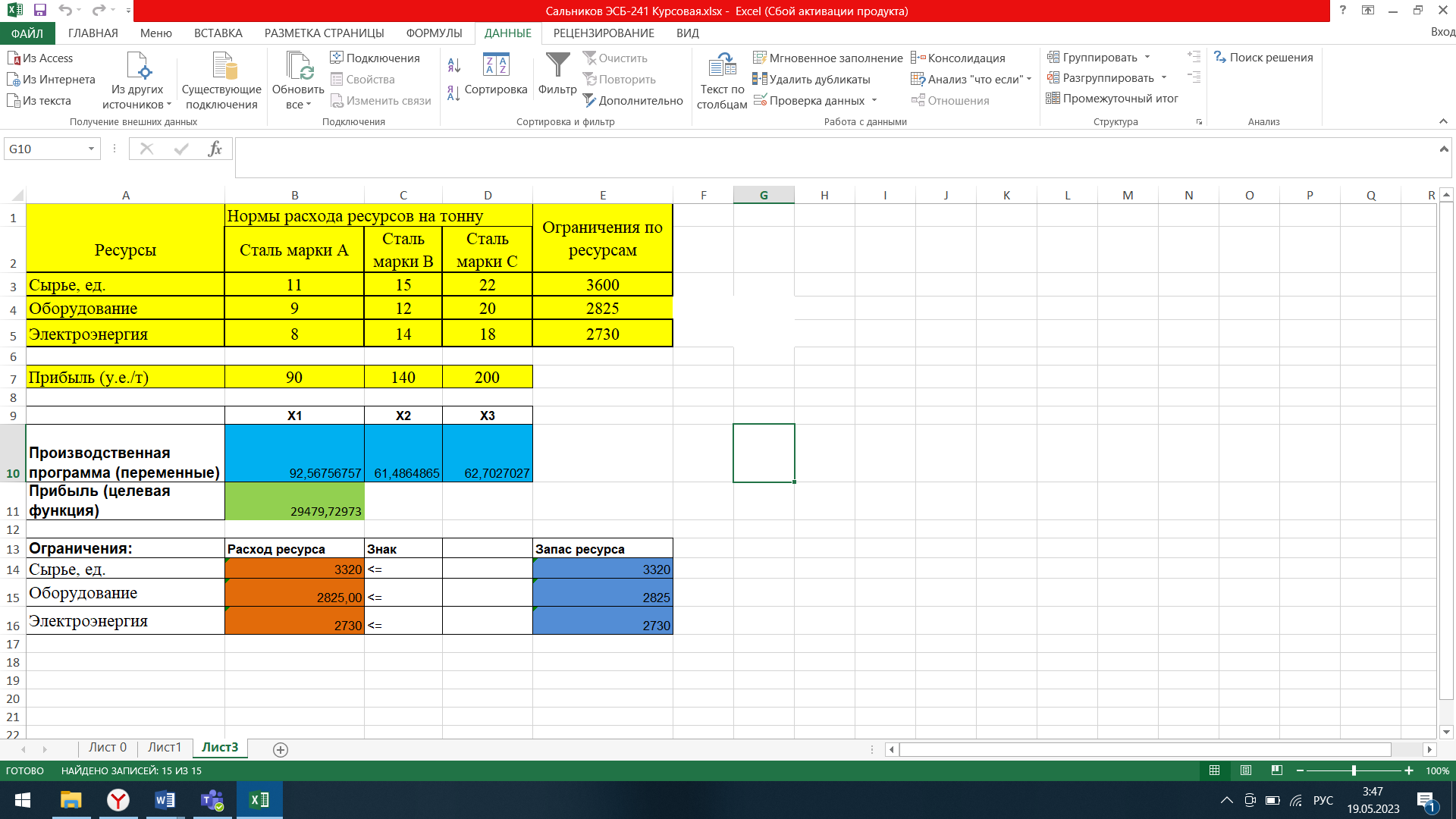Получим следующие результаты:Рис. 2.6. Таблица с увеличением запасов.Г) При уменьшении прибыли стали марки А на 9 (Сальников) и поиску оптимального решения, произойдёт изменение производственной программы. 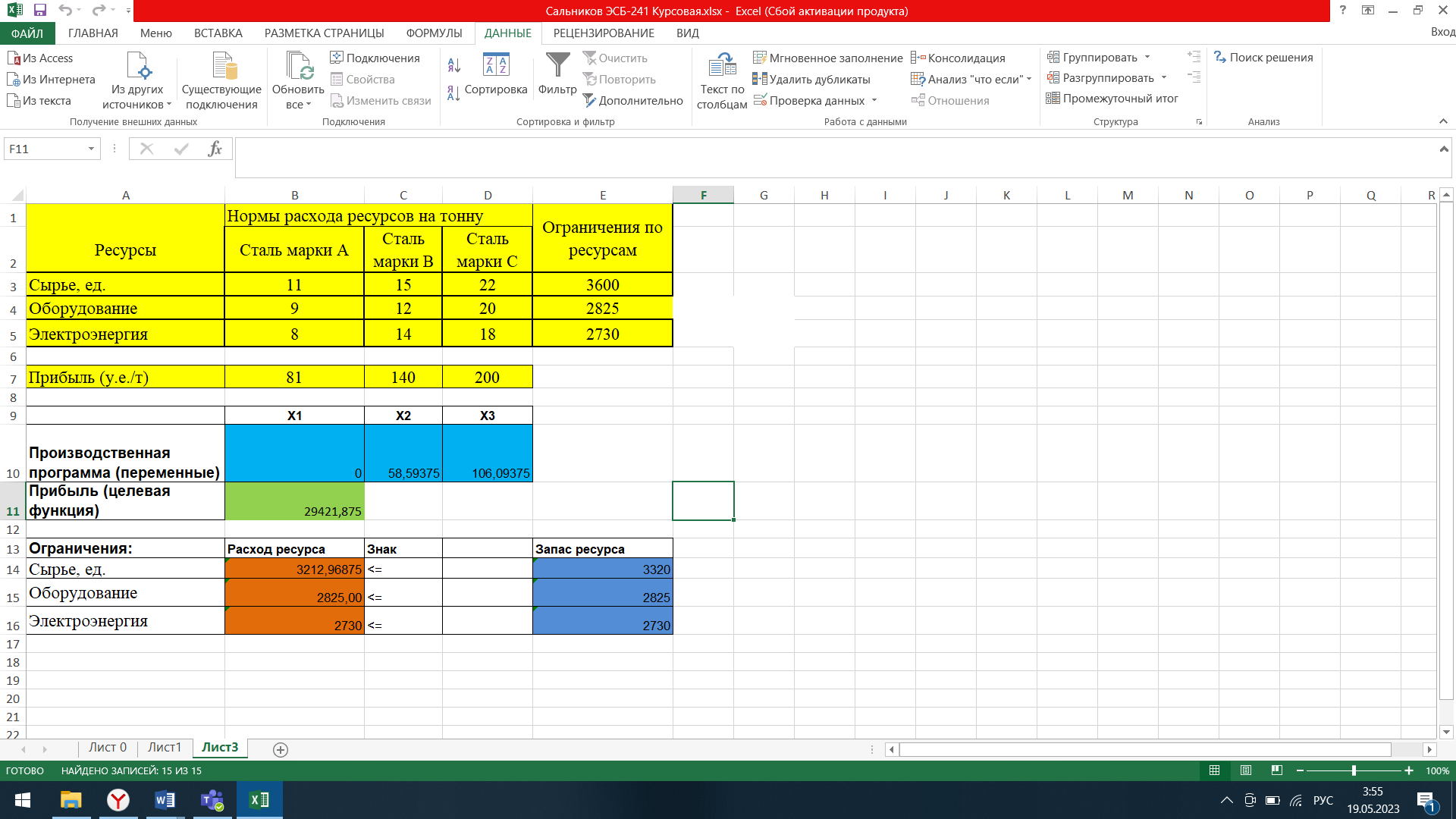Результаты будут следующие:Рис. 2.7. Таблица с уменьшением прибыли.По новой производственной программе будет производиться 0т. стали марки А, 58,59т. стали марки В и 106,09т. стали марки С, но, с последующим небольшим увеличением прибыли на – 29421,875 вместо 28200, что, несомненно, является положительным моментом.
ЗАКЛЮЧЕНИЕ
В курсовой работе рассмотрен вариант решения задачи оптимизационных экономических задач методами линейного программирования. Метод математического программирования является основным инструментом описания оптимальных решений. Оптимальным решением считается такой способ действия, который в наибольшей степени способствует достижению поставленной в задаче цели. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов.Благодаря математическому программированию мы можем рассчитать наиболее оптимальные варианты для производства. Можно сказать, ответить на вопросы «Что производить и в каких количествах?». Поэтому методы математического программирования так широко используются на различных производствах в наше время.В данной курсовой работе была рассмотрена и решена задача линейного программирования. Для решения был применён метод линейного программирования, а именно: графический метод и надстройка «Поиск решения» в Microsoft Excel.В данной курсовой работе были рассмотрены и решены основные задачи линейного программирования: задачи оптимизации производства, задача составления смеси и составления расписания. Для решения данных задач были применены методы линейного программирования, а именно: графический метод и симплекс-метод, а также использовалась надстройка Microsoft Excel «Поиск решения».В результате выполнения работы были сформированы математические модели задач, были получены решения с помощью графического метода, симплекс-метода и надстройки «Поиск решений» в MSExcel, а также проведён анализ полученных данных.
Список литературы
-
Ишханян М.В., Фроловичев А.И. Методы оптимальных решений: учебное пособие. – М.: МИИТ, 2015. – 132 с. -
Соловьев В. И.Методы оптимальных решений: Учебное пособие. М.: Финансовый университет, 2012. 364 с. -
Методы оптимальных решений: учебное пособие / Н. С. Матвеев, Н. А. Никитина, Л. В. Ярыгина ; М-во образ. и науки РФ, Вологод. гос. ун-т. – Вологда : ВоГУ, 2017. – 92 с.