Файл: Министерств.docx

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)»

Институт Экономики и Финансов

Кафедра «Информационные системы цифровой экономики»

Курсовая работа

по дисциплине «Методы оптимальных решений»

на тему

«Модели организации и планирования производства»

Вариант №20

Выполнил:

Студент гр.ЭСБ-241 Сальников А.Д.

Проверил: доц. Фроловичев А.И.

Москва 2023

СОДЕРЖАНИЕ

Оглавление……………………………………………………………………………………1

Введение…………………………………………………………………………..2

Основная часть……………………………………………………………............3

Кейс-задание №1…………………………………………………………….3

Математическая модель задачи………………………………………...4

Решение задачи графическим методом…………………………………5

Решение задачи с помощью надстройки «Поиск решения»………….7

Интерпретация результатов и общий вывод……………………………9

Кейс-задание №2В………………………………………………………....10

Математическая модель задачи………………………………………..11

Решение задачи линейного программирования симплексе-методом..12

---

Решение задачи линейного программирования с помощью надстройки «Поиск решения» MS Excel……………………………………………………..14

Исследование оптимального решения………………………………...16

Заключение……………………………………………………………………….19

Список литературы………………………………………………………………20

 

ВВЕДЕНИЕ

Человеческая деятельность связана с принятием множества решений по способам достижения поставленных целей. При принятии решений приходится учитывать много факторов, таких как: ограниченность ресурсов, неопределённость внешних условий, присутствие конкурирующих сторон, которые стремятся достичь своих целей, не всегда совпадающих с нашими.

Если в какой-то системе (экономической, организационной, управленческой) имеющихся в наличии ресурсов не хватает для эффективного выполнения запланированной задачи, то возникают распределительные задачи. Цель решения таких задач – отыскание оптимального распределения ресурсов по работам. Под оптимальностью распределения может пониматься, например, минимизация общих затрат, связанных с выполнением работ, или максимизация получаемого в результате общего дохода. Для решения таких задач используются методы математического программирования.

Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения.

Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования.

Линейное программирование — это наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения. По типу решаемых задач методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Целью данной курсовой работы является овладение математическими методами решения экономических задач. Задачи курсовой работы:

• 
  освоить графический метод решения задачи линейного программирования
  
• 
  научиться строить экономико-математические модели основных типов задач линейного программирования и решать данные задачи с помощью надстройки Microsoft Excel «Поиск решения»;
  
• 
  освоить симплекс-метод и метод решения задачи линейного программирования.
  

---

ОСНОВНАЯ ЧАСТЬ

Кейс-задание №1

Предприятие может выпускать две марки стали: сталь марки А и сталь марки B. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.

Недельные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены финансовыми средствами, емкостью складских помещений, логистическими ограничениями и т.д., по оборудованию – плавильными мощностями и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице 1.

Ресурсы	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
	Сталь марки A	Сталь марки B
Сырье, ед.	0,55k	0,75k	3200+20k
Оборудование	0,45k	0,6k	2100+30k
Электроэнергия	0,4k	0,7k	2100+25k
Прибыль (у.е./т)	90	140

Исходная таблица. Таблица 1.

	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
Ресурсы	Сталь марки A	Сталь марки B
Сырье, ед.	11	15	3600
Оборудование	9	12	2700
Электроэнергия	8	14	2600
Прибыль (у.е./т)	90	140

---

Таблица со значениями из варианта. Таблица 2.


Требуется сформировать недельную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной. Для этого предлагается:

1. Составить математическую модель данной задачи

2. Решить задачу линейного программирования графическим методом; 

3. Решить задачу линейного программирования с использованием надстройки «Поиск решения» MS Excel; 

4. Провести интерпретацию результатов и сделать выводы. 

 

​1. Математическая модель данной задачи 

1) критерий – максимум прибыли 

2) переменные 

x₁ – количество стали марки А

x₂ – количество стали марки В

3) целевая функция – максимизация прибыли

Z(x) = 90 x₁ + 140 x₂ -> max

4) система ограничений

Целевая функция:

Z(X) = 90х₁+140х₂max

Ограничения по запасам ресурса на три вида продукции.

Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2. Правая часть ограничения – это их запас ресурса.

Получаем следующие ограничения:
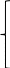- по сырью:

11х₁ + 15х₂ ≤ 3600

- по оборудованию:

9х₁ + 12х₂ ≤ 2700

- по электроэнергии:

8х₁ + 14х₂ ≤ 2600
Вид математической модели:

Z(X) = 90х₁+140х₂  max




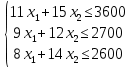
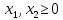
2. Решение задачи линейного программирования графическим методом

​Решение графическим методом означает, что нужно построить прямые по каждым неравенствам и определить полуплоскости. 

​Z(x) = 90 x₁ + 140 x₂ -> max

​

Соблюдая алгоритм, решим ЗЛП графическим методом:

1) Построение ОДР (область допустимых решений). Для построения графической системы необходимо решить неравенства. Для этого приравняем каждое из неравенств и решим их по отдельности.

---

1)

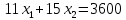
х1	0	300
х2	240	20

2)

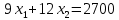
х1	300	0
х2	0	225

3)

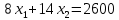
х1	325	150
х2	0	100

2) Вектор градиента целевой функции. Исходя их нашей целевой функции задачи Z(X) = 90х₁+140х₂  max, можем найти вектор-градиент. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Начало вектора – точка (0; 0), конец – точка (90;140).

grad = (90;140)


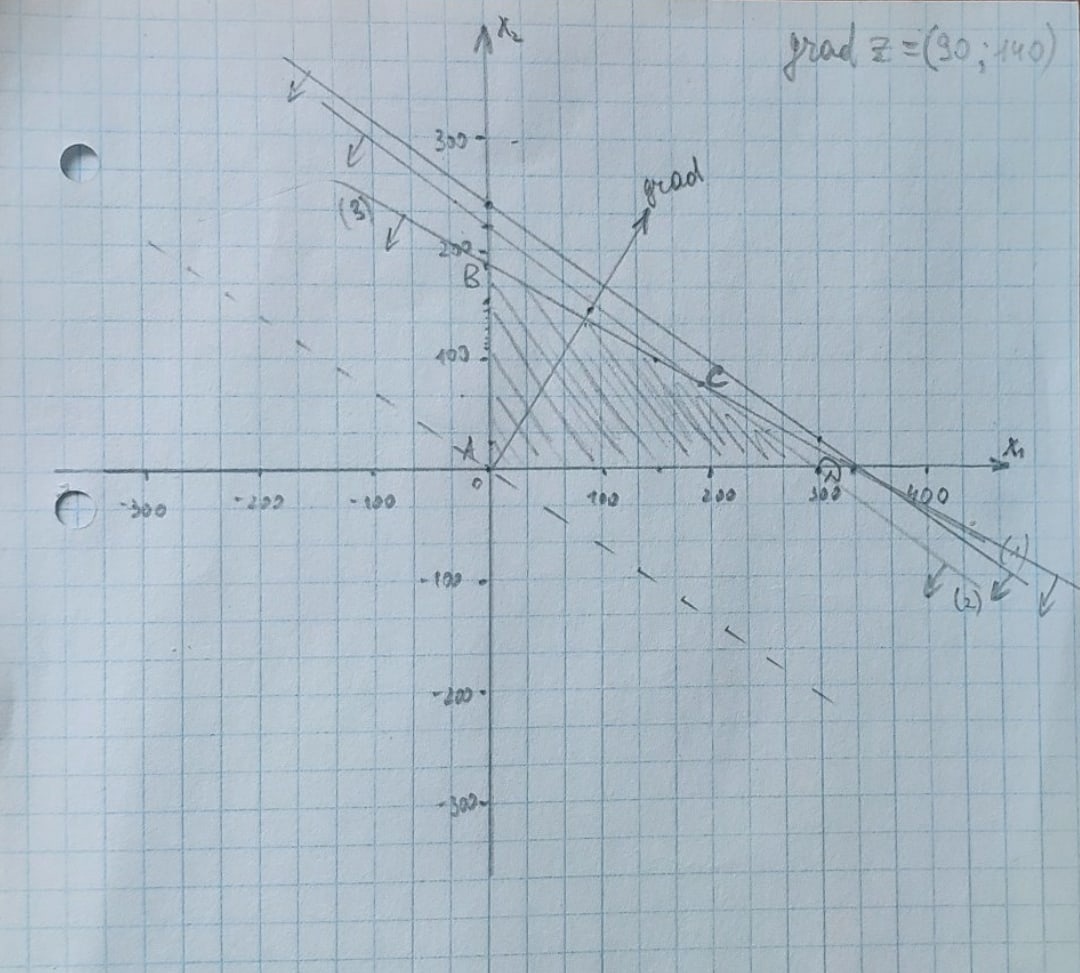
Рис.1.1 (график)

3) построение линий уровня целевой функции и нахождение экстремальной точки:

90 x₁ + 140 x₂ =0

Х_max = С

4) определение точки экстремума аналитически:

Х_max = (2) 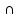(3)



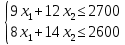
x₁ =220; x₂ =60

Z_max = 90*220+ 140 * 60 = 28200

Ответ: x₁ =220; x₂ =60; Z_max = 28200

Вывод: при объеме выпуска 220 тонн стали марки А и 60 тонн стали марки В, прибыль составит 28.200 у.е.

3. Решение задачи линейного программирования спомощьюнадстройки«Поиск решения»MSExcel.

Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.



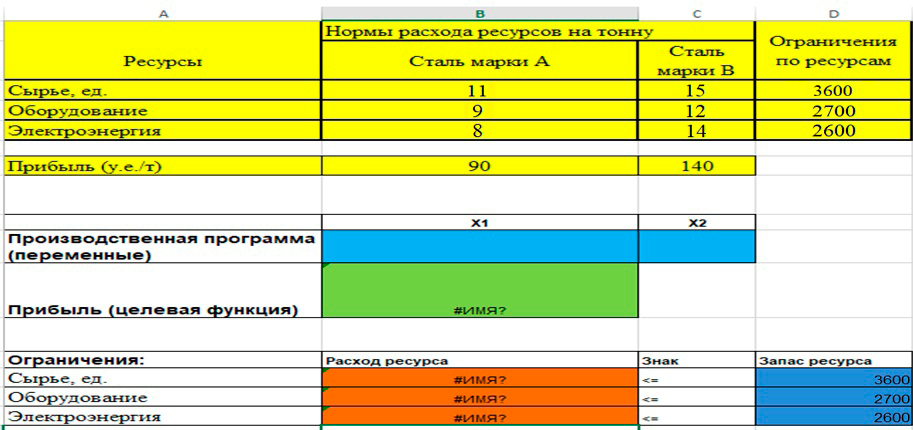
Рис.1.2. (Исходные данные в табличной модели)

В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие.

---