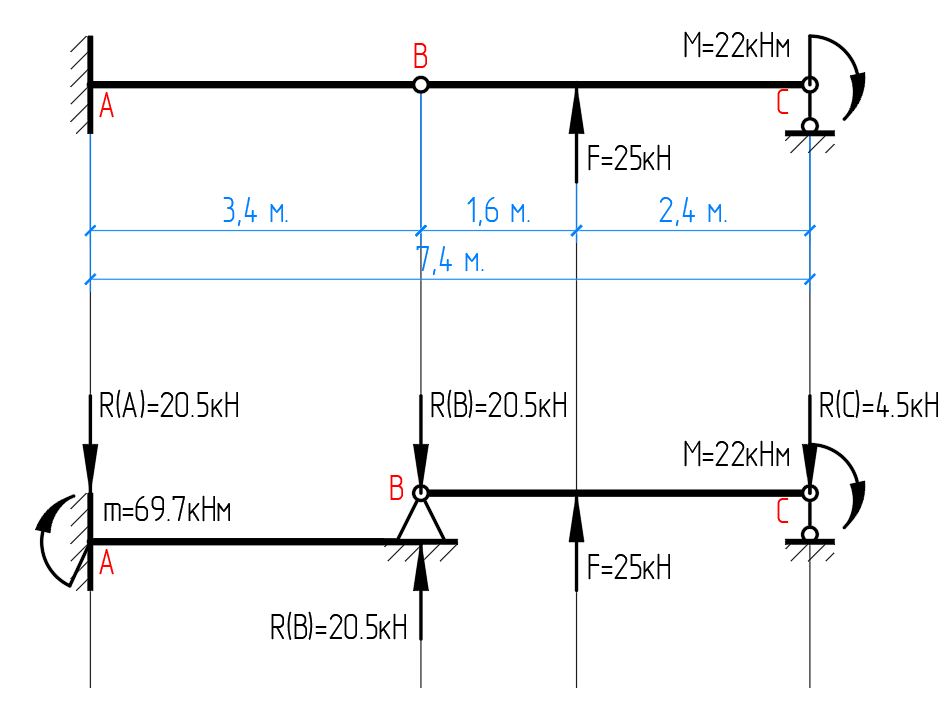
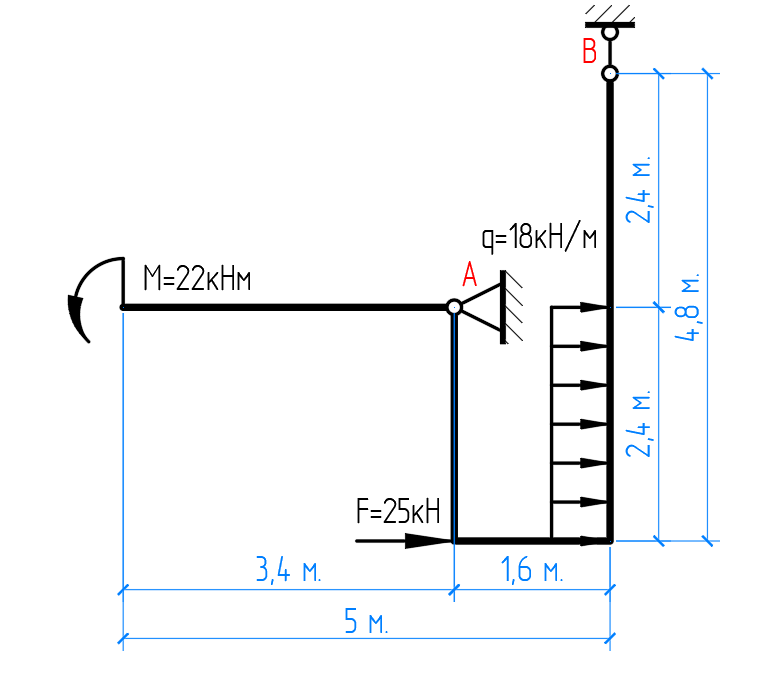
ЗаданиеДля заданных расчетных схем (см. рис. 1, 2) определить реакции опор.Исходные данныеРасчетная схема балки – схема 2, Расчетная схема рамы – схема 9,F = 25 кН, M = 22 кН, q = 18 кН/м;a = 3.4 м, b = 1.6 м, c = 2.4 м;I_р/I_с = 3/1 – для рамы. Для балки I = const;Рисунок 1сверху – расчётная схема балкиснизу – расчётная схема рамыРасчётДля расчетной схемы многопролётной балки построю поэтажную схему и для каждой балки найду реакции опор. 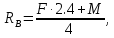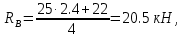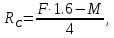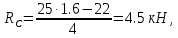Так, для верхней балки реакции опор нахожу при помощи уравнений сумм всех моментов относительно опор C и B:Σm_C = 0 = F·2.4 + M – R_B·4;Σm_B = 0 = F·1.6 – M – R_C·4;Выразив из этих уравнений неизвестные, получаю значения неизвестных реакций:Проверю правильность вычисления опорных реакций для верхней балки путём записи уравнения сумм всех сил относительно вертикальной оси:Σz = 0 = F – R_B – R_C;Σz = 0 = 25 – 20.5 – 4.5 = 0;Следовательно, реакции опор для верхней балки найдены верно.Аналогично рассчитываю реакции опор для нижней балки, учитывая действие верхней балки на нижнюю только с обратным знаком. Σm_{заделки} = 0 = m – R_B·3.4бΣz = 0 = R_A + R_B;Тогда:m = R_B·3.4 = 20.5·3.4 = 69.7 кНм,R_A = R_B = 20.5 кН;Расчётная схема многопролётной балки с найденными реакциями опор для каждой балки представлена на рисунке 2.Рисунок 2 – Найденные реакции опор для многопролётной балкиДля расчетной схемы рамы реакции опор нахожу при помощи уравнений сумм всех моментов относительно опоры A и точки K, а также составлю уравнение сумм всех сил на горизонтальную ось:Σm_A = 0 = F·2.4 + M + 0.5·q·2.4² – R_B·1.6;Σm_K = 0 = F·2.4 + M + 0.5·q·2.4

---

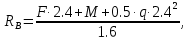
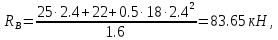
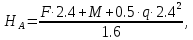
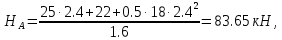
² – H_A·1.6;Σx = 0 = q·2.4 + F – R_A; Выразив из этих уравнений неизвестные, получаю значения неизвестных реакций:R_A = q·2.4 + F = 18·2.4 + 25 = 68.2 кН;Проверю правильность вычисления опорных реакций для рамы путём записи уравнения сумм всех моментов относительно точки L:Σm_L = 0 = F·4.8 + M + q·2.4·3.6 – R_A·2.4 – R_B·0.8 – H_A·0.8 = = 25·4.8 + 22 + 18·2.4·3.6 – 68.2·2.4 – 83.65·0.8 – 83.65·0.8 = 0;Следовательно, реакции опор для рамы найдены верно.Расчётная схема рамы с найденными реакциями опор для каждой балки представлена на рисунке 3.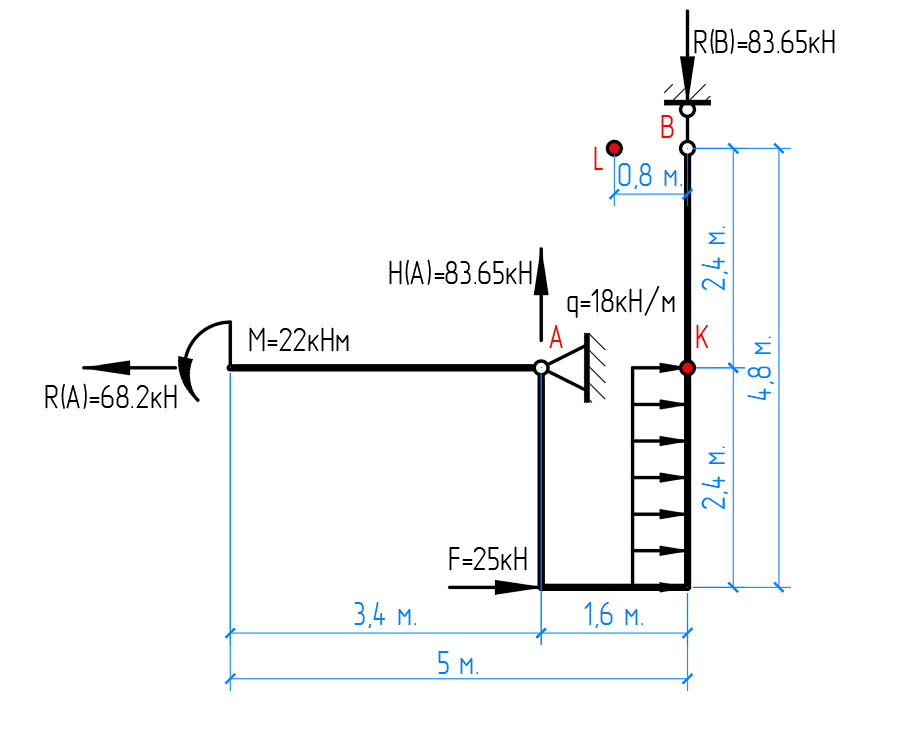Рисунок 3 – Найденные реакции опор для многопролётной балки

---

Смотрите также файлы

• Система управления персоналом организации.doc

• 1. Эдмунт амбиверсияны сынды Адамны оамдаы іс рекетін зерттейтін леуметтік психология Оыту жне трбиелеу психологиясы андай ылыммен байланысты Педагогика кемшіліктер ымы Адлер 5.docx

• С алат с копчёной курицей.rtf

• Используя учебную и научную литературу, нормативные правовые акты (со ссылками на них) ответьте на следующие вопросы.doc

• Ситуация с инклюзивным образованием в некоторых странах мира. Страна мира на выбор обучающегося.docx