Файл: Расчёт электрического поля, усилий, энергии и электрических параметров простейших конструкций.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 30

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

________________________ВШЭНиГ_____________________________

(наименование высшей школы / филиала / института / колледжа)

КОНТРОЛЬНАЯ РАБОТА №1

По дисциплине/междисциплинарному курсу/модулю
Физические основы электротехники







На тему
Расчёт электрического поля, усилий, энергии и электрических параметров простейших конструкций









Выполнила обучающаяся:




(Ф.И.О.)




Направление подготовки / специальность:

13.03.02 Электроэнергетика и электротехника




(код и наименование)




Курс: 2




Группа: 243706





Руководитель:

Баланцев А.Р.


(Ф.И.О. руководителя, должность / уч. степень / звание)




Отметка о зачете



















(отметка прописью)



(дата)

Руководитель


















(подпись руководителя)



(инициалы, фамилия)

Архангельск 2019

СОДЕРЖАНИЕ



1 Расчёт электрического поля, усилий, энергии и электрических параметров простейших конструкций
3

    1. Цель задания
3

1.2 Содержание задания
3

2 Задание №1
4

3 Задание №4
10


1 РАСЧЁТ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, УСИЛИЙ, ЭНЕРГИИ И ЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ ПРОСТЕЙШИХ КОНСТРУКЦИЙ
1.1Цель задания

Целью задания является закрепление теоретического материала, излагаемого в первой части курса – физические основы электротехники (ФОЭ). Теоретическая часть расчётов базируется на уравнениях поля в интегральной форме. Особенности конструкций элементов (сферическая и цилиндрическая симметрия) существенно упрощают расчётную часть и позволяют при выполнении задания сосредоточить внимание на физической стороне процессов.

1.2 Содержание задания

В соответствие с буквенной литерой (А, m – 1, n – 3) выбирается расчётный вариант, заданный геометрией элемента, номерами условий задания и номерами самого задания в соответствии с таблицей 1
Таблица 1




2 ЗАДАНИЕ №1

Найти зависимости электрического смещения D, напряжённости электрического поля Е, поляризованности Р и потенциала U в произвольной точке как функции расстояния r (d). Начало отсчёта (r или d = 0) считать в центре сфер или на оси цилиндрических поверхностей (в плоском конденсаторе от верхней пластины).

Построить графики зависимостей 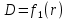; ; 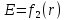; 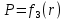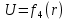и объяснить характер их изменений во всех областях и на границах этих областей.

Найти выражения объёмной плотности энергии электрического поля 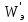во всех областях. Построить график
.
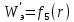Решение

По объему проводящего заряженного шара однородно распределен заряд q.

Внутри проводящего шара (область 1) поле отсутствует.

Найдём зависимость электрического смещения . Основа для расчёта – постулат Максвелла: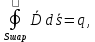
(1.1)
где 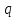- объемная плотность заряда,

V – объем заряженного проводящего шара.

В силу симметрии поля смещение и напряженность на поверхности нулю, т.е.

,

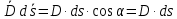тогда



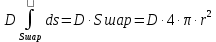
Тогда из вышеприведенного постулата Максвелла получим:





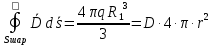
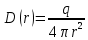
Это выражение справедливо в пределах от 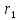до бесконечности. Так как область 2 и область 3 – диэлектрики.

Напряжённость электрического поля найдём из соотношения.

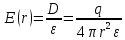(1.2)

Вектор 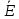также совпадает с направление .

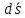Поляризованность диэлектрика в области 2 и в области 3 можно определить на основе выражения (1.3):





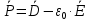
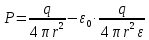
Окончательно:

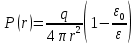(1.3)

Для определения потенциала электрического поля воспользуемся выражением, принимая потенциал внутри заряженного шара равным нулю. Поскольку вектор 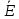совпадает по направлению с 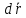, выражение перепишем в виде

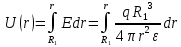(1.4)

Путь интегрирования от R1 до произвольной точки r проходит в областях с различной диэлектрической проницаемостью
, то при переходе из области 2 в область 3 подынтегральная функция меняется скачком.

Поэтому при



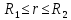
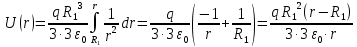
При


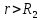
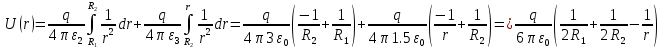
Для построения графиков подставим известные постоянные значения.

Из условия задачи найдем





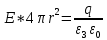
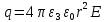
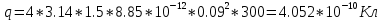
Определим объёмную плотность энергии электрического поля.

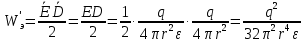(1.5)

Таблица 2

R, см
0
3
3
3,5
4
4,5
5
5,5



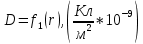0,00
0,00
35,84
26,33
20,16
15,93
12,90
10,66



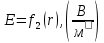0,00
0,00
1350,02
991,85
759,39
600,01
486,01
401,66



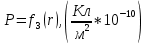0,00
0,00
23,90
17,56
13,44
10,62
8,60
7,11



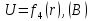0,00
0,00
0,00
5,79
10,13
13,50
16,20
18,41



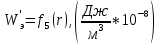0,00
0,00
241,94
130,60
76,55
47,79
31,36
21,42


Таблица 3

R, см
6
6,5
7
7,5
7,5
8
8,5
9



8,96
7,64
6,58
5,73
5,73
5,04
4,46
3,98



337,50
287,58
247,96
216,00
432,01
379,69
336,34
300,00



5,97
5,09
4,39
3,82
1,91
1,68
1,49
1,33



20,25
21,81
23,14
24,30
24,30
26,33
28,11
29,70



15,12
10,98
8,16
6,19
12,39
9,57
7,51
5,97



Ниже изображены графики – эпюры полученных зависимостей с указанием номера области.

На графике объёмной плотности энергии видно, что при переходе из области 2 в область 3 происходит скачёк, что объясняется скачкообразным изменением свойств среды на границе двух диэлектриков.

Смотрите также файлы