Файл: Геометрические вероятности. Имитационное компьютерное моделирование вероятностных опытов.docx
Добавлен: 30.11.2023
Просмотров: 56
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
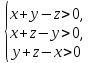
Область куба, где выполняются все три условия, можно представить на рисунке
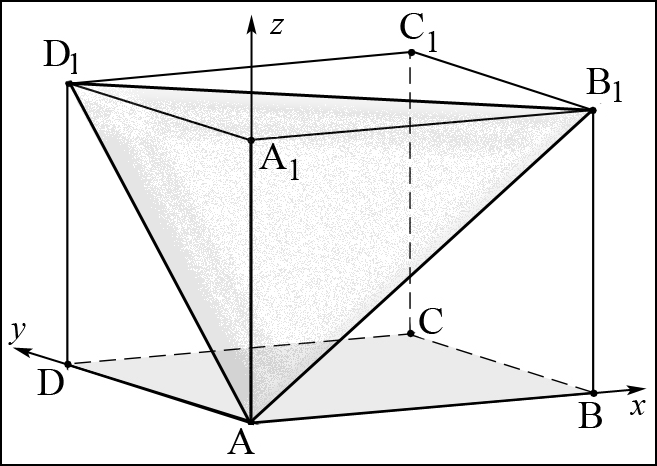
Здесь заштрихованная плоскость соответствует уравнению
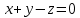, а области, противоположной первому неравенству, соответствует пирамида с основанием 
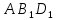и вершиной 
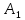. Можно подсчитать, что ее объем равен 
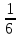. Аналогично неравенством, противоположным второму, отрезается область с вершиной 
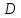тоже объемом 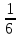. Неравенством, противоположным третьему, отрезается область с вершиной 
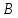тоже объемом 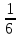. Таким образом, отрезается объем, равный 
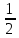, а значит оставшийся объем равен 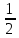и все точки этой области удовлетворяют всем трем «неравенствам треугольника».Значит, искомая вероятность равна
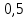.Проведем имитационное компьютерное моделирование вероятностных опытов.
Для этого потребуется следующее.
1°. С помощью генератора случайных чисел генерируем три случайных числа 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 и 0 ≤ y ≤ 1. Это можно сделать с помощью функции rnd() языка VBA (встроен в MS Excel).
2°. Напишем программу, которая на основе этих чисел проверяет выполнение трех «неравенств треугольника». В случае успеха счетчик успехов
увеличиваем на единицу.Программу на языке Visual Basic for Applications (разновидность VB, встроенная в MS Excel), осуществляющей моделирование, приведем ниже.
Sub Лаб_2()
' Лаб_2 Макрос
Dim i, n, k As Long
Dim ii As Integer
Dim l1, l2, l3 As Double
' Ввод числа экспериментов
n = Cells(2, "A")
Randomize
k = 0
' Генерация трех сторон треугольника
For i = 1 To n
l1 = Rnd()
l2 = Rnd()
l3 = Rnd()
' Проверка условий существования треугольника
If l1 < l2 + l3 And l2 < l1 + l3 And l3 < l1 + l2 Then k = k + 1
Next i
ii = 2
Do While Cells(ii, "C") <> ""
ii = ii + 1
Loop
' Вывод результатов эксперимента
Cells(ii, "C") = n
Cells(ii, "D") = k
Cells(ii, "E") = k / n
End Sub
3°. Находим относительную частоту события F – «Треугольник существует» по формуле w(F) =
. Меняя число n имитационных опытов, будем получать соответствующие частоты событий 
и соответствующие относительные частоты w = .Результаты и обсуждение.
Результаты каждого имитационного опыта заносим в итоговую отчетную таблицу и строим ломаную линию относительных частот в сопоставлении с теоретической вероятностью события F.
Результаты имитационного моделирования задачи о существовании треугольника:
| n | lg(n) | k | p |
| 50 | 1,699 | 24 | 0,48 |
| 500 | 2,699 | 260 | 0,52 |
| 5000 | 3,699 | 2541 | 0,5082 |
| 50000 | 4,699 | 24999 | 0,49998 |
| 500000 | 5,699 | 250387 | 0,500774 |
| 5000000 | 6,699 | 2499140 | 0,499828 |
| 50000000 | 7,699 | 25000313 | 0,500006 |
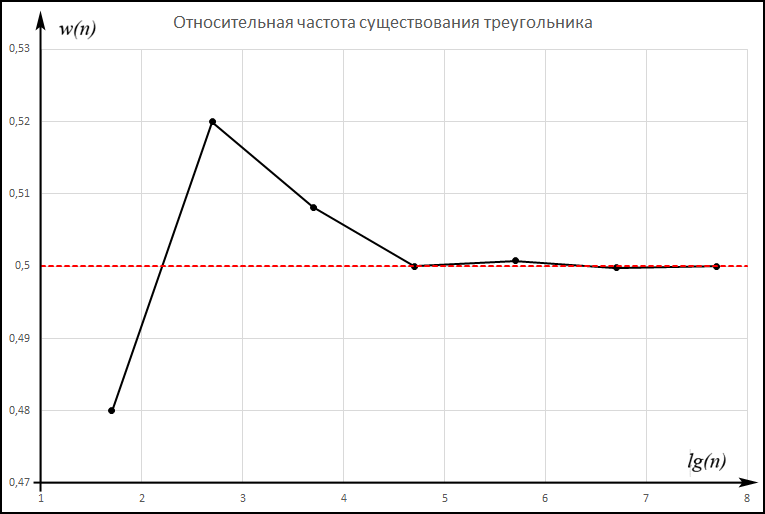
Выводы.
Для заданного случайного события вычислена теоретическая вероятность, используя геометрическое определение вероятности в пространстве. Написана программа имитационного моделирования, которая при большом числе испытаний (формально при n → ∞) подтвердила, что относительные частоты стремятся к теоретической вероятности события F, равной 0,5.
Список цитированной литературы.
[1] Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высшая школа [издания разные лет].
[2] Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974. – 124 с. URL: https://b-ok.cc/dl/2339066/a9821b
[3] Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. М.: Айрис-Пресс, 2004. – 256 с.
[4] Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 2004. – 572 с. URL: https://studizba.com/files/show/pdf/40466-3-a-n-kolmogorov-s-v-fomin--elementy.html
3° Самостоятельное решение упражнений с оформлением в виде файла MS Word
В а р и а н т I.
З а д а ч а I.1°. Весной катер идёт против течения реки в 2⅔ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1½ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Решение.
Введем неизвестные:
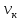– собственная скорость катера (в неподвижной воде), 
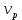– скорость течения реки весной. Тогда уравнение для весны: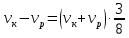
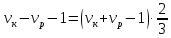
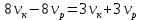
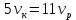
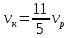
Уравнение для лета:
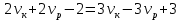
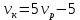
Приравниваем скорости катера:
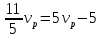
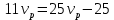
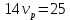
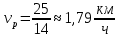
Ответ:
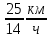.З а д а ч а I.2°. Вездеход, находящийся на пересеченной местности в 27 км от прямолинейной шоссейной дороги, должен доставить геологов в населенный пункт, расположенный на шоссе. Расстояние от точки шоссе
, ближайшей к вездеходу, до населенного пункта равно 45 км. По пересеченной местности вездеход двигается со скоростью 44 км/ч, а по шоссе – 55 км/ч. На каком расстоянии от населенного пункта вездеход должен выехать на шоссе, чтобы время движения было наименьшим?
Решение.
Рассмотрим схему движения вездехода:
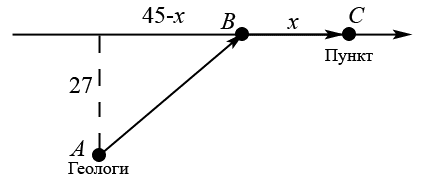
Введем неизвестное
- расстояние BC от точки выхода вездехода на шоссе до населенного пункта. Тогда дорога по пересеченной местности равна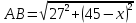
Общее время движения вездехода равно
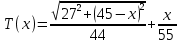
Вычислим производную от этой функции
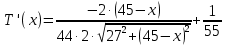
Решим уравнение:
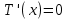
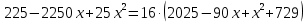
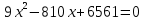
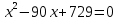
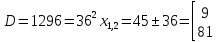
Значение 81 км слишком велико, не подходит под условия задачи.
Рассмотрев окрестность точки
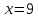, видим, что производная меняет знак с минуса на плюс, значит найденная точка – минимум функции 
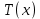.Ответ:
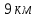.З а д а ч а I.3°. Двум дорожно-строительным бригадам поручено строительство шоссейной дороги между пунктами А и В. В течение 40 дней бригады работали отдельно, сначала первая, потом вторая, причем одна из них выполнила 1/3, а другая 1/6 всей работы. На 41 день бригады стали работать совместно и оставшуюся часть дороги построили за 18 дней. Определить, за сколько дней каждая бригада, работая отдельно, могла бы построить шоссе.
Решение.
Введем неизвестные:
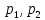– производительности бригад с размерностью, равной доли всей работы, выполненной в день, - дн. – работала первая бригада отдельно,
дн. – работала вторая бригада отдельно. Составим уравнения: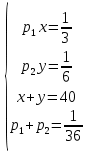
Последнее уравнение вытекает из условия, что две бригады (с производительностью
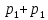) выполнили за 18 дней половину всей работы.Выразим из третьего уравнения
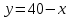и подставим во второе: 
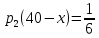.Первое уравнение умножим на
: 
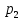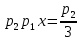, новое второе умножим на 
: 
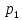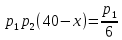и сложим: 
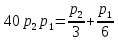.Из последнего уравнения выразим
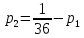и подставим в предыдущее.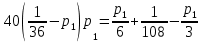
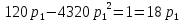
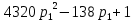
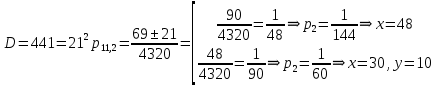
Подходит ответ:
, 
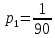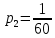
Ответ: первая бригада, работая отдельно, могла бы построить шоссе за 90 дней, вторая бригада, работая отдельно, могла бы построить шоссе за 60 дней.
З а д а ч а I.4°. При изготовлении консервной банки цилиндрической формы заданной вместимости V требуется металл двух видов: на боковую поверхность – I сорта, на основания – II сорта, стоимость которого в 2 раза меньше, чем стоимость I сорта. При каком отношении высоты банки к радиусу ее основания затраты на металл будут наименьшими?
Решение.
Введем
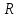– радиус основания цилиндра, 