Пифагордың шалбары,

Соңымыздан қалмады.

Ышқыры кең, ауы тік,

Бір балағы тар-дағы.

Осы бұрынғы оқулықтардағы теореманы негізге ала отырып, мен Пифагор теоремасын дәлелдеуді тік бұрышты үшбұрыштың гипотенузасын 3 – тен басталатын натурал сан, алкатеттерін нақты сандар жиынында қарастырдым. Яғни

с ˆ Ν, а ˆ R , в ˆ R .
IІІ тарау.

Пифагор теоремасын дәлелдеу
Теореманың қарапайым дәлелдеуі

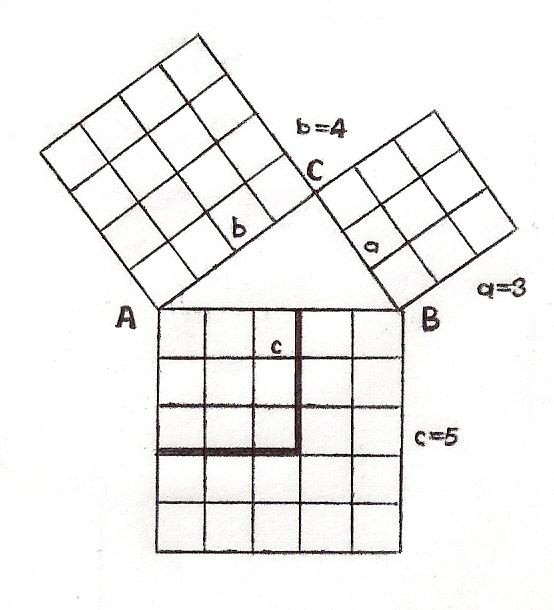
Тік бұрышты үшбұрыштың гипотенузасына салынған квадрат катеттеріне салынған квадраттардың қосындысымен тең шамалы. Теореманың қарапайым дәлелдеуі тең бүйірлі үшбұрыш жағдайында қарастырылады. Теореманың өзі де осыдан басталған.

Теореманың дұрыстығына көз жеткізу үшін тең бүйірлі тікбұрышты үшбұрыштар мозаикасына қарау жеткілікті. Мысалы, ΔABC үшін : АС гипотенузасына салынған квадрат 4 үшбұрыштан құралған, ал катеттерге салынған квадраттардың әрқайсысы екі үшбұрыштан тұрады. Теорема дәлелденді.

Теореманы алгебралық әдіспен дәлелдеу

Т - катеттері а, b және гипотенузасы с болатын тікбұрышты үшбұрыш болсын. с2=а2+b2 екенін дәлелдеу керек.

Қабырғалары а+b -ға тең Q квадратын саламыз. Q квадратының қабырғаларынан А, В, С, D нүктелерін, пайда болған АВ, ВС, CD, DA кесінділері катеттері а және b –ға тең Т1, Т2, Т3, Т4 тікбұрышты үшбұрыштар құратындай етіп саламыз. ABCD тіктөртбұрышын Р деп белгілейміз. Енді Р қабырғалары с-ға тең квадрат екенін көрсетуіміз қажет.

Барлық Т1, Т2, Т3, Т4 тік бұрышты үшбұрыштары Т тік бұрышты үшбұрышына тең (екі катеті бойынша). Сондықтан олардың гипотенузалары Т тікбұрышты үшбұрышының гипотенузасына, яғни с кесіндісіне тең. Енді бұл төртбұрыштың бұрыштары тік екенін дәлелдейміз.

және - Т үшбұрышының сүйір бұрыштары. Онда + = 90° екендігі белгілі. Р төртбұрышының А төбесіндегі бұрышы , бұрыштарымен қоса жазыңқы бұрышты құрайды. Сондықтан + + =180°. + = 90° болғандықтан =90°. Р төртбұрышының басқа бұрыштарының да тік екендігі дәл осылай дәлелденеді. Осыдан, Р төртбұрышы қабырғасы с болатын квадрат екендігі шығады.

Қабырғасы а+b –ға тең Q квадраты қабырғасы с-ға тең Р квадраты мен Т үшбұрышына тең төрт үшбұрыштан тұрады. Сондықтан олардың аудандары үшін S(Q)=S(P)+4S(T)орындалады.

S(Q)=(a+b)2;

S(P)=c2 және

S(T)=½a*b өрнектерін S(Q)=S(P)+4S(T) теңдігіне қою арқылы 

---

(a + b)2 = c2 + 4*½a*b теңдігін аламыз. (

(a+b)2=a2+b2+2*a*b болғандықтан (a+b)2=c 2+4*½a*b теңдігін мына түрде жазуға болады: a2+b2+2*a*b=c2 +2*a*b.

a2+b2+2*a*b=c2+2*a*b теңдігінен с2=а2+b2 тең екендігі шығады.

Фигуралардың тең шамалылығын пайдала отырып дәлелдеу

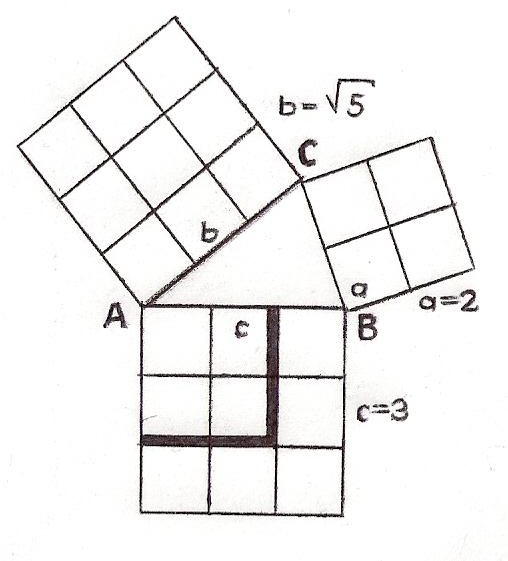
Берілген тікбұрышты үшбұрыштың гипотенузасына салынған квадрат катеттерге салынған квадраттар құрастырылған фигуралардан тұратынын дәлелдеуді қарастыруға болады. 2 суретте екі тең квадраттар бейнеленген. Әрбір квадраттың қабырғаларының ұзындығы а + b-ға тең. Квадраттардың әрбіреуі квадраттар мен тікбұрышты үшбұрыштардан тұратын бөліктерге бөлінген.Егер квадрат ауданынан катеттері а және b-ға тең тік бұрышты үшбұрыштың 4 еселенген ауданын алып тастасақ, онда тең шамалы аудандар қалады, яғни c2 = a2 + b2 . Бұл дәлелдеуді ұсынған ежелгі үндістер дәлелдеуді жазбаған, тек сызбаны «қара!» деген сөзбен түсіндірген.

Аддитивті дәлелдеулер

Бұл дәлелдеулер катеттерге салынған квадраттар жіктелген фигуралардан гипотенузаға салынған квадратты құрастыруға болатынына негізделген.

• 
  Энштейн дәлелдеуі: гипотенузаға салынған квадратты 8 үшбұрыштарға бөлуге негізделген.
  

Бұл жерде: ABC –тікбұрышы С болатын тікбұрышты үшбұрыш. C MN; CK MN; PO||MN; EF||MN.

• 
  Пифагор теоремасын Евклидтің «Бастамалар» шығармасының ортағасырлық бағдадтық комментаторы ан-Найризия ұсынған бөлулер көмегімен дәлелдеу келтірілген. Бұл жағдайда гипотенузаға салынған квадрат 3 үшбұрышқа және 2 төртбұрышқа бөлінген.Мұнда: ABC – тікбұрышы C болатын үшбұрыш; DE = BF.
  

ан-Найризияның дәлелдеуінің негізінде квараттарды қос-қостан тең болатын фигураларға бөлуге де болады ( 5-сурет, бұл жерде ABC – C бұрышы тік болатын тікбұрышты үшбұрыш.).

• 
  Квадраттарды тең бөліктерге жіктеу әдісі арқылы тағы бір дәлелдеу «қалқаншалы дөңгелек» деп аталады және 6-суретте көрсетілген. Мұнда: ABC– тікбұрышы C болатын тікбұрышты үшбұрыш; O – үлкен катетке салынған квадраттың центрі, О нүктесі арқылы өтетін пунктирлі түзулер гипотенузаға перпендикуляр немесе параллель.
  

Қосымша салулар арқылы дәлелдеу.

Бұл әдістің негізі тең шамалы фигуралар пайда болу үшін катеттерге салынған квадраттарға және гипотенузаға салынған квадратқа тең фигуралар салынады.

• 
  қарапайым Пифагор фигурасы, яғни қабырғаларына квадрат салынған АВС тікбұрышты үшбұрышы бейнеленген. Бұл фигура алдыңғы тікбұрышты үшбұрышқа тең 1 және 2 үшбұрыштарымен толықтырылады.
  

---

Пифагор теоремасының дұрыстығы AEDFPB және ACBNMQ алтыбұрыштарының тең шамалы екендігінен шығады. Мұнда C EP, EP түзуі AEDFPB алтыбұрышын екі тең шамалы төртбұрыштарға, CM түзуі ACBNMQ алтыбұрышын екі тең шамалы төртбұрыштарға бөледі, А центрімен жазықтықты 90° бұрсақ АЕРВ төртбұрышы АСМQ төртбұрышына беттеседі.

• 
  Пифагор фигурасы қабырғалары катеттерге салынған квадраттар қабырғаларына параллель тіктөртбұрышқа толықтырылады.Бұл тіктөртбұрыш үшбұрыштар мен тіктөртбұрыштарға бөленеді. Пайда болған тіктөртбұрыштан 1,2,3,4,5,6,7,8,9 көпбұрыштарын алып тастаймыз, сонда гипотенузаға салынған квадрат қалады. Енді осы тіктөртбұрыштан 5,6,7 және штрихталған тіктөртбұрыштарды алып тастасақ, катеттерге салынған квадрат пайда болады. Енді бірінші жағдайда алып тасталған фигуралар мен екінші жағдайда алып тасталған фигуралар тең шамалы екендігін дәлелдейміз.
  
• 
  Нассириддин (1594 ж. ) дәлелдеуі көрсетілген. Мұнда: PCL – түзу;
  

KLOA = ACPF = ACED = a2; LGBO = CBMP = CBNQ = b2; AKGB = AKLO + LGBO = c2; бұдан c2 = a2 + b2.

• 
  Гофман (1821 ж.) дәлелдеуі. Мұнда : ABC -тік бұрышы С болатын тікбұрышты үшбұрыш; BF кесіндісі CB кесіндісіне перпендикуляр және тең, BE кесіндісі AB кесіндісіне перпендикуляр және тең, AD кесіндісі AC -ға перпендикуляр және тең; F, C, D нүктелері бір түзудің бойында жатады; ADFB және ACBE төртбұрыштары теңшамалы, өйткені ABF=ECB; ADF және ACE үшбұрыштары тең шамалы; енді екі тең шамалы төртбұрыштан да екеуіне ортақ АВС үшбұрышын алып тастаймыз, сонда мына теңдікті аламыз:
  

Алгебралық әдіспен дәлелдеу.

• 
  Ұлы үнді математигі Бхаскаридің дәлелдеуі.
  
• 
  ABC – тік бұрышы С болатын тікбұрышты үшбұрыш, CM AB, b1 – гипотенузаға түсірілген b катетінің проекциясы, a1 – гипотенузаға түсірілген а катетінің проекциясы, h – үшбұрыштың гипотенузаға түсірілген биіктігі.
  

ABC үшбұрышы мен ACM үшбұрышының ұқсастығынан

b2 = cb1; (1)

ABC , BCM үшбұрыштарының ұқсастығынан

a2 = ca1. (2) шығады. (1) және (2) теңдіктерін мүшелеп қоссақ, a2 + b2 = cb1 + ca1 = c(b1 + a1) = c2 теңдігін аламыз.

• 
  Мёльманн дәлелдеуі -1 әдісі.
  

Тікбұрышты үшбұрыштың ауданы -ға немесе -ға тең, мұнда p – үшбұрыштың жарты периметрі, r – үшбұрышқа іштей сызылған шеңбердің радиусы Осыдан:

c2=a2+b2. теңдігі шығады.

Мёльманн дәлелдеуі-2 әдісі Тікбұрышты үшбұрыштың ауданы :S=½*a*b немесе S=½(p*r) тең (кез-келген үшбұрыш үшін);

p - үшбұрыштың жарты периметрі ; r – Іштей сызылған шеңбердің радиусы.

---

r = ½*(a + b - c) – кез-келген үшбұрышқа іштей сызылған шеңбер радиусы.

½*a*b = ½*p*r = ½(a + b + c)*½(a + b - c);

a*b = (a + b + c)*½(a + b - c);

a + b=x;

a*b = ½(x + c)*(x - c)*a*b = ½(x2-c2)

a*b = ½(a2 + 2*a*b + b2 - c2)

a2 + b2 - c2 = 0, сондықтан

a2 + b2 = c2

Гарфилд дәлелдеуі.

Үш тікбұрышты үшбұрыш трапеция құрап тұр.Сондықтан бұл фигураның ауданын тікбұрышты трапецияның ауданы бойынша немесе үш тікбұрышты үшбұрыштың аудандарының қосындысы бойынша табуға болады. Екеуін теңестіре келе, c2=a2+b2 екендігі шығады.

Бұрыштың косинусын пайдалана отырып дәлелдеу.

ΔАВС – С бұрышы тік болатын берілген тіктөртбұрыш.С тікбұрышының төбесінен СD биіктігін жүргіземіз.

Косинустар теоремасының анықтамасы бойынша (Тікбұрышты үшбұрышың сүйір бұрышының косинусы деп іргелес жатқан катеттің гипотенузаға қатынасын айтамыз.) соsА=AD/AC=AC/AB. Бұдан AB*AD=AC2. Осыған ұқсас соsВ=BD/BC=BC/AB. Бұдан шығатыны AB*BD=ВС2. Шыққан теңдіктерден AD+DB=AB екенін ескере отырып, АС2+ВС2=АВ(AD + DB)=АВ2 теңдігін аламыз. Теорема дәлелденді.

Евклид дәлелдеуі

Берілгені:ΔАВС – тікбұрышты үшбұрыш, AJ - гипотенузаға түсірілген биіктік, BCED – гипотенузаға салынған квадрат, ABFH және ACKJ - катеттерге салынған квадраттар.

Дәлелдеу керек: Гипотенузаның квадраты катеттерінің квадраттарының қосындысына тең.(Пифагор теоремасы).

Дәлелдеуі:

1. BJLD тіктөртбұрышы ABFH квадратына тең шамалы екендігін дәлелдеу керек. ΔABD=ΔBFS (екі қабырғасы мен арасындағы бұрышы бойынша BF=AB; BC=BD; Бұрыш FBS=бұрышABD). SΔABC=½SBJLD, өйткені ΔABC үшбұрышы мен BJLD тіктөртбұрышында BD ортақ табан және LD ортақ биіктік. Осыған ұқсас SΔFBS=½SABFH (BF-ортақ табан, AB – ортақ биіктік). Осыдан SΔABD= SΔFBS екендігін ескере отырып, SBJLD=SABFH теңдігін аламыз. ΔBCK және ΔACEүшбұрыштарының теңдігін пайдала отырып, SJCEL=SACKG екендігі дәлелденеді. Бұдан SABFH+SACKJ=SBJLD + SBCED.

Дәлелдеулердің бірнеше түрлерін қарастыра келе, мына суреттер бойынша қосымша салулар арқылы дәлелдеулер келтірілген. Мұнда пунктирлі сызықтар қосымша салуларды көрсетеді.

Сонымен ежелгі египеттіктер қабырғалары 3,4,5 болатын үшбұрышты 2000 жыл бұрын тік бұрыш салуға пайдалана білген. Яғни Пифагор теоремасына кері теореманы қолданған. Енді үшбұрыштар теңдігінің белгілеріне негізделген дәлелдеуді келтірейік. Сонымен ABC үшбұрышының қабырғалары( 24-сурет) c2 = a2 + b2. (3) қатынасымен байланысты. Осы үшбұрыштың тікбұрышты үшбұрыш екенін дәлелдейміз. Катеттері берілген үшбұрыштың a және b катеттеріне тең болатын екі катеті бойынша A1B1C1 үшбұрышын саламыз (25- сурет). Салынған үшбұрыштың гипотенузасы c1 тең болсын. Салынған үшбұрыш тікбұрышты үшбұрыш болғандықтан Пифагор теоремасы бойынша c12 = a2 + b2. (4) (3) және (4) теңдіктерін салыстыра отырып , c12 = c2, немесе c1 = c екендігін аламыз. Осыдан берілген және салынған үшбұрыштар үш қабырғалары сәйкесінше теңболғандықтан үшбұрыштардың теңдігі шығады. Пифагор теоремасының дәлелдемелерін көптеп келтіруге болады.

---

1-Тәсіл.



Бірінші, гипотенуза 3 см болсын. Сонда Пифагор теоремасының формуласы бойынша 3? = a? + b? болады. 3 см – ге тең гипотенуза бойынша, катеттердің өлшемдерін жуықтап есептеу тәсілімен a= 2 см , b = √5 см деп аламын. Пифагор теоремасы бойынша формула

немесе 9=4+5 натурал сандарына түрленеді.Бұл теңдіктің оң жағын қоса отырып, (4+5) квадраттардың аудандары 3 см – лік гипотенузаға салынған квадраттың ауданына тең шамалы екенін көреміз, яғни 9 см? = 9 см?
2-Тәсіл.


^{Гипотенуза 5см-ге тең болса, аналитикалық теңдеу :} берілген үшбұрыш бойынша: 5?= а?+b? жуықтап есептеу тәсілі бойынша 5² = √9 + √16 = 3? + 4?, квадраттарды есептесек 25 = 9+16. Квадраттың ауданы см? түрінде берілгенде, тікбұрышты үшбұрыш гипотенузада 5 см-ге тең, оның а = 3см; b = 4см-ге тең катеттерінде құрылған.

---

Смотрите также файлы

• Отчет о прохождении производственной практики (преддипломной) в период с 20 г по 20 г. Специальность 43. 02. 11 Гостиничный сервис.pptx

• Тарауы Аудан.docx

• Практическое задание по дисциплине Экономическая теория.docx

• В случае заключения контракта с смп или сонко по результатам закупки в соответствии с п. 1 ч.docx

• Противопожарное водоснабжение.docx