25 = 9+16 теңдігінде үшбұрыштың катеттерінде орналасқан екі шаршының ауданын см? түрінде аламыз. Бұл гипотенузада орналасқан шаршының ауданына тең. Яғни 25 см? = 25см? екенін дәлелдедік.

3-Тәсіл.

Бұл суретте тікб ұрышты ∆АВСгипотенузасы 6 см болатын үшбұрышқа с әйкес катеттерін жуы қтап есептейміз. Сонда катеттерге салынған квадраттардың аудандарының қосындысын гипотенузадағы квадраттың ауданына тең болуы керек. Аналитикалық теңдеу: мынадай түрге айналады,

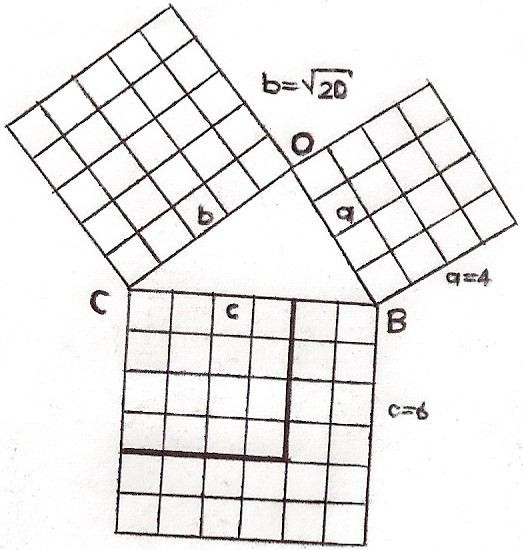
Катеттердің квадраттарының ауданын қосу арқылы, үлкен квадраттың ауданын табамын, ол сөзсіз гипотенузада орналасқан квадраттың ауданына тең. 36 см? = 36см?екені дәлелденді.

---

IV тарау.

Қолданыстағы Пифагор теоремасы
Пифагор теоремасы қазіргі өмірде құрылыста, астрономияда, мобильді байланыста кеңінен қолданылады. Суретте осы теореманы пайдалана отырып, готикалық стильде салынған терезенің мысалы келтірілген.

Сол сияқты шатыр салуда, найзағай түсірмеуге арналған құрылғыны салу үшін де осы теоремаға сүйенеді. Яғни, Пифагор теоремасы бойынша

h²≥ a²+b², яғни h≥(a²+b²)1/2.

Осы сияқты өмірде Пифагор теоремасын қолданатындығына көптеген мысалдар келтіруге болады.

Табиғат пен адам санасы біртұтас принциппен байланысты бол ғандықтан, ежелгі ұлы ғалымдар яғни, Пифагор, Евклид, Архимед, Аристотельдердің дәлелдеген ғылым жетістіктері әлі күнге дейін адамзат баласына қызмет етіп келеді. Табиғаттың басты принциптерін түсіну арқылы бұл заңдардың табиғат пен адам санасының бір – бірімен ты ғыз байланыста болатынын білдім. «Байланыс» деген сөз философия категориясының құрамына кіріп, шексіз тығыз байланыста болады. Адам сан асының дамуы арқылы Пифагор теоремасы дәлелденді.

Пифагор теоремасы – геометрияның аса ма ңызды теоремаларының бірі. Көптеген теоремалар мен формулалар сол арқылы дәлелденеді. Олардың кейбіреулері:

1. Сүйір бұрышқа қарсы орналасқан қабырға туралы теорема.

2. Доғал бұрышқа қарсы орналасқан қабырға туралы теорема.

3. Үшбұрыштың ауданын есептеуге арналған Герон формуласы.

4. Екі нүктенің ара қашықтығының формуласы.

5. Призма, параллелепипед,пирамида жөніндегі теоремалар.

Бұл тізімді әрі қарай жал ғастыра беруге болады. Пифагор теоремасы өмірде жиі қолданылады, оның кездеспейтін жері аз. Сондықтан оны математик қана емес, әрбір мәдениетті адам білуі қажет.

Осы ғалымдардың еңбектері өмірде жиі қолданылып, математика –

дәлелденген ғылым болып табылды.

Ертеден келе жатқан өте ыңғайлы және дәл тәсіл, жер өлшеушілермен перпендикуяр сызықтарды жүргізу үшін қолданылған тәсіл.

3:4:5 қатынасы бәріне белгілі Пифагор теоремасы.




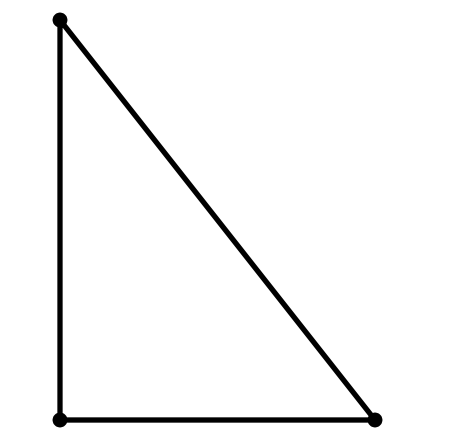
Теорема бойынша:

3²+4²=5²

---

3,4,5 сандарынан басқа шексіз бүтін а,b,с

а²+b²=с²

бар екені айқын.
Олар Пифагор сандары деп аталады . Пифагор теоремасы бойынша бұл сандар тік бұрышты үшбұрыштың қабырғаларының ұзындықтары болып табылады. а және в қабырғалары катет, с гипотенуза деп аталады.

Егер а,b,с пифагор санының үштігі екені белгілі болса, онда ра, рb, рс болса.

Мұңдағы р – бүтін санды көбейткіш Пифагор сандары болып табылады Керісінше, егер Пифагор сандарның ортақ көбейткіштері бар болса , онда осы ортақ көбейткіштерді қысқартуға болады және тағы пифагор санының үштігін аламыз.

Сондықтан ең бірінші қарапайым пифагор саны үштігінің өзара байланыстылығын зерттеу керек, қалғаны оларды р бүтін санды көбейткіштерге көбейту деп шығады .

а,b,с үштігінде оның бір катеті жұп сан, ал 2–ші катеті тақ сан болатынын көрсетейік. Кері дәлелдеуді қолдансақ: егер 2 катеті де а және в жұп сан болса онда а²+b² саны да жұп болады, ал ол гипотенуза. Бұлай болуы мүмкін емес, себебі а, b, с сандарының ортақ көбейткіштері болады деген ұғымға қайшы келеді, үш сан жұп болса оның ортақ көбейткіштері 2-еу болады .

Олай болса, а, в катеттің бірі тақ сан болады деген қорытындыға келуге болады.

Егер 2 катет тақ сан, ал гипотенузасы жұп болады деп қарастырсақ. Бұлай болуы мүмкін емес. Шындығында егер катеттер 2х+1 және 2у+1 болса онда олардың квадратарының қосындысы мынаған тең:
4х²+4х+1+4у²+4у+1=4(х²+х+у²+у)+2
Яғни 4-ке тең бөлгенде 2 қалдық қалады. Кез келген жұп санның квадраты 4 санына қалдықсыз бөлінуі керек. Ендеше екі тақ санның квадратарының қосындысы жұп санының квадраты болуы мүмкін емес, басқаша бұл үш сан пифагор саны болмайды.

Сонымен а,в катеттерінің біреуі жұп, екіншісі тақ сан болады .с гипотенузасы тақ сан болады . Егер а катеті тақ , в катеті жұп болса деп алсақ.

а²+b²=с² теңдігінен

а²=с²-b² формуласы бойынша

а²=(с-b)(с+b)

(с+в) және (с–в) көбейткіштері өзара жай сан . Шындығында, осы сандар ортақ көбейткіштері бар болса, бірден өзгеше, онда осы көбейткіштер және қосындысы да ортақ көбейткішке бөлінер еді.

---

(с+b)+(с– b)=2с және айырмасы

(с+b) – (с– b)=2b ал көбейттіндісі

(с+b)(с– b)=2а тең болады .

2с,2в және а ортақ көбейткіштері бар болған болар еді.

Егер а жұп болса онда бұл көбейткіш 2-ден өзгеше, сондықтан осы ортақ көбейткіш а,в,с сандары үшін мүмкін емес. (с+в) және (с– в) сандары өзара жай сан деген ұғымға қарама-қайшы келеді.

Егер өзара жай санның көбейттіндісі дәл сан квадраты болса, онда олардың әрқайсысы санның квадратына тең.

Пифагор сандары үшін дәлелдеусіз мына қорытындыға келуге болады:

1) катеттің біреуі 3-ке еселі.

2) катеттің біреуі 4-ке еселі.

3) Пифагор сандарының біреуі 5-ке еселі.

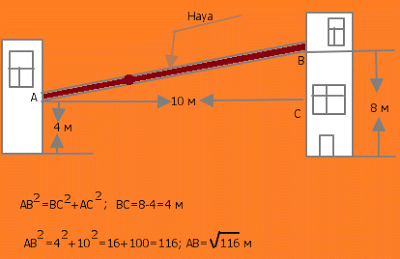
Есеп 1. Материал тасымалдау үшін фабриканың екі үйінің арасынан көлбеу науа жасалған. Бұл екі үйдің ара қашыұтығы 10 м -ге тең,ал науаның екі басы жер бетінен 8 м және 4 м биіктікте.Науаның ұзындығын тап.(А.В.Погорелев. Геометрия оқулығынан)

Шешу: 

Есеп 2.Тең бүйірлі үшбұрыштың бүйір қабырғасы 17 см,ал табаны 16 см. Үшбұрыштың табанына түсірілген биіктікті тапбыңдар.(А.В.Погорелевтің геометрия оқулығынан.)

Шешуі:


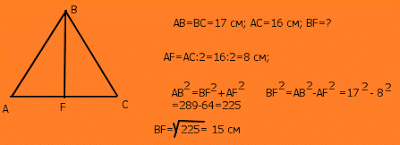
Есеп 3. Үшбұрыштың бүйір қабырғалары 30 см және 25 см,ал табанына түсірілген биіктігі 24 см.Үшбұрыштың биіктігін табыңдар.(А.В.Погорелевтің геометрия оқулығынан)

Шешуі:


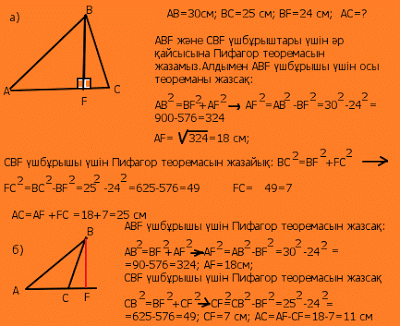
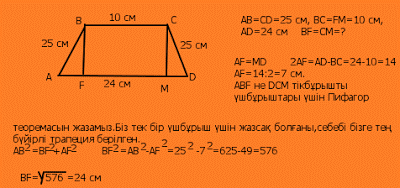
Есеп 4. Тең бүйірлі трапецияның табандары 10 см-ге және 24 см-ге тең,бүйір қабырғасы 25 см.Трапецияның биіктігін табыңдар.(А.В.Погорелевтің геометрия оқулығынан)

Шешу:



 Есеп 5.Үшбұрыштың қабырғалары а,b,c. Үшбұрыштың с қабырғасына түсірілген биіктігін тап.

Шешуі:


Қорытынды

Мен жұмысымды қорытындылай жұмыста қойылған мақсатқа жеттім деп ойлаймын. Басты мақсат – қолданыстағы Пифагор теоремасының технологиясының ерекшелігі.

Мен ұсынып отырған жұмысымда қолданыстағы Пифагор теоремасына берілген есептерін шешуге дайындау технологияларының үлгілері келтірілген. Осы технологияларды толық меңгерген оқушы міндетті түрде кез келген есепті шеше алатын болады. Сонымен қатар, оқушылардың бұл бағыттағы дайындық деңгейін дамыта түсу мақсатында жаттығу жүргізуге арналып біраз әртүрлі өмірлік есептер ұсынылған. Мұндағы басты мақсатымыз оқушылардың бойындағы ойлану, іздену, талдаулар жүргізе білу қасиеттерін қалыптастыру және өз беттерінше шығармашылық тұрғыда жұмыс істеуге дағдыландыру.

---

Жоғарыда атап өткендей, мұндағы басты кеңес мыналар болады:

• 
  бастапқы кезде әртүрлі қолданыстағы Пифагор теоремасына берілген есептерді шешуге дайындау технологиясын толығына аяғына дейін талдап шығу;
  
• 
  әр кезеңнің және міндетін жете түсіну қажет болады.
  

Қазақ педагогикасының математикалық астарлары да түрліше. Олар біресе жұмбақ, біресе өлең, біресе қарасөз, біресе ертек, біресе ілмек, біресе дұзақ, біресе сиқырлы ой айту тағы басқа түрде кездеседі. Халық есептерінің өзімен туыстас, жалғас, көршілес елдердің салт-санасымен астарласып, үндесіп, қабысып жататындығы бар.

Барған жерін Балқан тау, 

О да біздің көрген тау, -демекші, қытайдың буы, орыстың ну-фуы, қазақтың түуі түп тамырлас.

Қолданыстағы Пифагор теоремасын математика курсында пәнаралық байланыс өте кең дамыған. Соның ішінде әдебиет пәнімен байланысты байқауға болады. Қандай есепті алсақ та, мақал немесе нақыл сөзбен түйінделген. Бұл түйіндеулерге зер салсақ, әрқайсысының тәрбиелік мәні зор. Тәрбие - сан қырлы. Ата-тегінің табысын айту, халқыңның дәстүрін сақтау, оны өз заманыңның қағидаларымен шендестіру тәрбиенің бір көзі.

Жұмысымды қорытындылай келе айтарым бүгінде жаһандану заманында жас ұрпаққа әлемдік стандартқа сәйкес білім беру мәселесі республикамызда ғылыми-педагогикалық тұрғыда ізденіспен әлемдік жинақталған тәжірибеге, отандық қол жеткен табыстарды саралай отырып, ұлттық ерекшеліктерді ескере, оқыту мен тәрбелеуді жаңаша ұйымдастыру көкейкесті мәселе болып отыр. Осыған орай ғылыми техникалық прогрессия дамыған уақытта қолданыстағы Пифагор теоремасына берілген есепті шешу технологиясының ерекшеліктері туралы сөз қозғадық. Келешектің кез келген маманы компьютерді өз жұмысында тиімді пайдаланғысы келсе, онда ол өз саласы бойынша алға қойылатын проблемаларды тұжырымдай алуы тиіс.

Жұмысымды қорытындылай келе, қандай да болмасын оқушы үшін қиындық тудырған кезде есептің нәтижесін көргенде, оның өзгеше бір сезімге бөленіп, бір марқайып қалуына ұмтылу қажеттілігін туғызуға мүмкіндік жасауға пән мұғалімі жұмысының өз нәтижесі болатындығын атап өткім келеді.


Пайдаланылған әдебиеттер тізімі:

1. 
   Балаян Э.Н. – «555 олимпиадных и занимательных задач по математике».
   
2. 
   Петраков И.С. – «Математика для любознательных».
   
3. 
   Республикалық ғылыми – әдістемелік журнал «Математика» №2 (2010).
   
4. 
   Республикалық ғылыми – әдістемелік журнал «Математика» №2 (2012).
   
5. 
   Рахымбердиев А. – «Оқушылардың математикаға қызықтыру». – Математика және физика журналы. - №2. – 2009.
   
6. 
   Ким Е. – «Нестандартные уроки математики». 5-6 классы. Поурочные планы. Волгорад «Аст». 2005.
   
7. 
   Бидосов Ә. Орта мектепте математиканы оқыту методикасы. – (1-басылым). - Алматы, «Мектеп» 1989.
   
8. 
   Әбілқасымова А. Е. Математиканы оқытудың теориясы мен әдістемесі. – Алматы, «Білім», 2005.
   
9. 
   Худайбергенова Н. Т. «Крест» таңдау әдісін теңдеулер мен теңсіздіктер шешуде қолдану.// «Математика» журналы №2, 2012, 38-39б.
   
10. 
    Мустафаев А.П. Теңдеулер әліппесі, Қазақ университеті. Алматы. 2004.
    
11. 
    Қаңлыбаев Қ. Теңсіздікке байланысты сан тізбектері.// «Математика» журналы №4, 2012, 14-18б.
    
12. 
    Кәрібаева С. «Модуль таңбасы бар теңсіздіктерді шешу» тақырыбын оқыту әдістемесі.// «Математика-Физика» журналы №1, 2007, 16-18б.
    
13. 
    Шөкімов С., Нәби Д. Көрсеткіштік және логарифифмдік күрделі теңдеулер мен теңдеулер жүйесін шешу.// «Математика-Физика» журналы №1, 2012, 5-6б.
    
14. 
    Ермаханова Г. Кейбір теңсіздіктерді теңдеулерді шешуге қолдану.// «Математика» журналы №1, 2011, 32-34б.
    
15. 
    Мамырбеков Т. Модуль таңбасы бар теңдеулердің кейбір дербес жағдайларын шешу тәсілдері.// «Математика-Физика» журналы №4, 2012, 16-17б.
    

---

Смотрите также файлы

• Отчет о прохождении производственной практики (преддипломной) в период с 20 г по 20 г. Специальность 43. 02. 11 Гостиничный сервис.pptx

• Тарауы Аудан.docx

• Практическое задание по дисциплине Экономическая теория.docx

• В случае заключения контракта с смп или сонко по результатам закупки в соответствии с п. 1 ч.docx

• Противопожарное водоснабжение.docx