14-ЛекцияЛекция тақырыбы: Салыстырулар теориясы және оның арифметикада қолданылуы. Жоспары:

1. 
   Негізгі түсініктер, салыстыру қасиеттері.
   
2. 
   Салыстырулар теориясын арифметикада қолдану.
   
3. 
   Қалындылардың толық жүйесі.
   
4. 
   Қалындылардың келтірілген жүйесі.
   
5. 
   Эйлер және Ферма теоремалары
   

1.Негізгі түсініктер, салыстыру қасиеттері. Салыстыру теориясы сандар теориясының бір бөлімі. 1795 жылы салыстырудың мәні мен символдық белгілеуін алғаш рет Гаусс енгізді. Оның зерттеу жұмысы 1801 жылы «Арифметикалық зерттеу» еңбегінде көрсетілген. Салыстыру жөніндегі ұғым бір санның екінші санға бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген сандардың бірі екіншісіне бөлінетін-бөлінбейтінін және де қандай қалдық қалатынын білу керек болғанда аса қажет болмақ. Математикада салыстыру теориясын көп жерде қолданады. Мысалы, салыстыру теориясы арқылы екі айнымалы бірінші дәрежелі теңдеуді шешуде, санды санға бөлгенде қалдықты табу, арифметикалық амалдың дұрыс орындалғандығын тексеру, жәй бөлшекті ондық бөлшекке айналдырғандағы период ұзындығын табу, тағы сол сияқты мәселелерде қолданады.Анықтама. a және b – бүтін сандар m модулі бойынша салыстырмалы деп аталады, егер a – b айырмасы m-ге бөлінетін болса.Сонда берілген a, b, m сандары арасындағы қатынасты салыстыру көрсетеді және m –маңызды рөл атқарғандықтан, біз оны «модуль» деп атаймыз. Қысқаша, бұл үш сандардың қатынасын мынандай түрде жазамыз:a 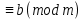(1).Ал a және b – салыстырудың оң және сол жақтары деп атайды. m саны әрқашан оң мәнге ие: m 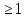және ол модуль таңбасымен жазылады: mod m. Егер a - b айырмасы m-ге бөлінетін болса, онда a 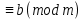түрінде, ал егер бөлінбейтін болса, a 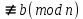түрінде жазамыз.Салыстыру қатынас:

1. 
   Рефлексивті, яғни a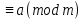
   
2. 
   Симметриялы, яғни a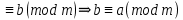
   
3. 
   Транзитивті, яғни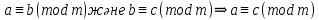
   

---

Осыдан салыстыру қатынасының эквивалентті қатынас екені көрінеді. Осы эквивалентті салыстыру қатынасы бүтін сандар жиынын эквивалентті қластарға бөледі, оларды m модулі бойынша қалындылар кластары деп атайды.

1. 
   Қалындылар кластарының кез келген екеуі қиылыспайды немесе беттеседі.
   
2. 
   А және В m модулі бойынша қалындылар кластары болсын. а€А, b€B. А және В бетеседі сонда тек сонда ғана, егерде ).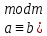
   
3. 
   А m модулі бойынша қалындылар класы және а€А болса, онда А=a+mZ, A={a+mk│ k€Z}.
   

Тұжырым. m модулі бойынша а және b сандары салыстырмалы болады, сонда тек сонда ғана, егер а және b сандарын m-ге бөлгенде олардың қалдықтары бірдей болса.Слыстырудың қасиеттері:

1. 
   Егер .
   
2. 
   Егер .
   
3.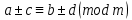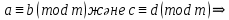 
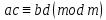   Егер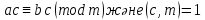 болса, онда .
   
4. 
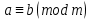   Салыстырудың екі жағын және модульді де олардың ортақ көбейткішіне бөлуге болады.
   
5. 
   Егер m₁ саны m санының бөлгіші және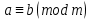 болса, онда .
   

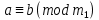2.Салыстыру теориясын арифметикада қолдану. Салыстырудың практикалық және теориялық мәнісі зор: бөлу амалын орындамай тұрып, берілген санның бірі екінші санға бүтіндей бөліне ме, егер бөлінбесе, қандай қалдықтын қалатынын тағайындау керек. Бұл жерде кез келген бүтін санның басқа бір санға бөлінуі үшін қажетті және жеткілікті шарттарды көрсету өте маңызды.Бұл мәселені жалпы түрде шешу қиынға соғады, кейбір жағдайлар үшін тек жеткілікті шарттарды ғана, яғни сандардың бөлінгіштік белгілерін ғана, көрсетуге болады. Біз енді сандардың 2-ге, 3 пен 9-ға, 4-ке, 5-ке, 7-ге, 11-ге, 13-ке бөлінгіштік белгілерін дәлелдейік. Француз математигі Паскаль сандар үшін бөлінгіштіктің ортақ белгісін тапқан.Теорема.

---

Кез келген q негізінде жазылған а натурал саны, яғни 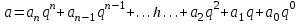түріндегі сан m санына бөліну үшін 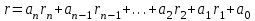санының m санына бөлінуі қажетті және жеткілікті.

Дәлелдеу Паскаль теоремасына негізделген 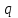санау системасындағ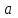ы саны.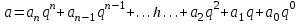

болсын, бұнда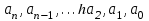 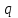санау ситемасының цифрлары және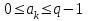 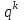санын модуль 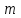бөлгендегі қалдық 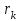болсын.

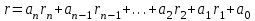белгілейік.

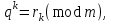болғандықтан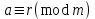

Бөлінгіштіктің Паскаль белгісі: а саны m-ге бөлінеді сонда, тек сонда егер 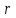m-ге бөлінсе.

1-Салдар m саны (q-1) санының бөлгіші болсын, онда q негізде жазылған сан m санына бөлінуі үшін оның цифрларының қосындысы m-ге бөлінуі қажетті және жеткілікті.

2-Салдар m саны (q+1) санының бөлгіші болсын, онда q негізде жазылған сан m санына бөлінуі үшін оның жұп және тақ орында тұрған цифрларының айырымы m-ге бөлінуі қажетті және жеткілікті.

3-Салдар m саны q^k санының бөлгіші болсын, онда q негізде жазылған сан m санына бөлінуі үшін оның соңғы k цифрларынан жасалған санның m-ге бөлінуі қажетті және жеткілікті.

Дербес жағдай ондық санау жүйесінде


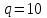
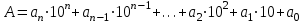
демек, ондық санау жүйесінде 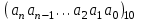деп жазылады.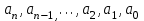





- - - - - - - - - - - - - - - - - - - - -

---

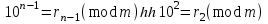
- - - - - - - - - - - - - - - - - - - - -Жоғарыдағы теорема мен келтірілген салдарлардан q=10 негізіндегі сандардың бөлінгіштік қасиеттерін алуға болады.2-ге бөлінгіштік белгісі. 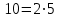болғандықтан, 5-қасиеттің салдары бойынша, былай болады: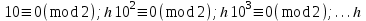Сондықтан, 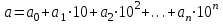саны 2-ге бөлінуі үшін, яғни 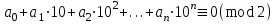орындалуы үшін, 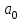санының 2-ге бөлінуі, яғни 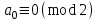орындалуы, қажетті және жеткілікті. Бұған қарап сандардың 2-ге бөлінгіштігінің мынандай оңай белгісін табамыз: саны 2-ге бөлінуі үшін, санындағы бірліктер санын білдіретін 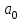-дің 2-ге бөлінуі қажетті және жеткілікті.3 пен 9 сандарына бөлінгіштік белгісі. 1-салдар бойынша: берілген саны 3-ке (9-ға) бөлінеді сонда, тек сонда егер санының жазылуындағы цифрларының қосындысы 3-ке (9-ға) бөлінсе. Шындығында, 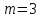(не 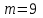) болса, 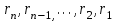, қалдықтары 1-ге тең. Демек, 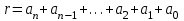. Онда Паскаль белгісінен 3-ке (9-ға) бөлінгіштік белгісінің дұрыстығы шығады.4-ке бөлінгіштік белгісі (3-салдар бойынша). 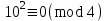болатын себепті, мына салыстыру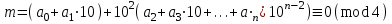орындалу үшін, мына шарт

---

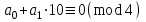
қажетті және жеткілікті. Бұған қарағанда, 4-ке бөлінгіштік белгісі мынандай болмақ:егер санының соңғы екі цифрын өрнектейтін сан 4-ке бөлінсе, онда санының өзі де 4-ке бөлінеді. Керісінше, егер саны 4-ке бөлінсе, онда санының соңғы екі цифрын өрнектейтін сан 4-ке бөлінеді.

5-ке бөлінгіштік белгісі (3-салдар бойынша). 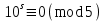болатын себепті, кез келген бүтін оң 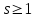болғанда, мына салыстыру

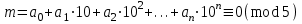орындалу үшін, мына шарт

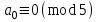жеткілікті.

Сонда 5-ке бөлінгіштік белгісі мынандай: егер санының соңғы цифры 5-ке бөлінсе, онда санының өзі де 5-ке бөлінеді.

11-ге бөлінгіштік белгісі (2-салдар бойынша).

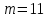болса,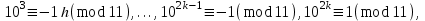



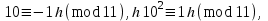
яғни



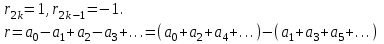
Онда Паскаль белгісінен қорытынды жасаймыз: Берілген саны 11-ге бөліну үшін жұп орындағы цифрлардың қосындысы мен тақ орындағы цифрлардың қосындысының айырымы 11-ге бөлінсе болғаны.

3.Қалындылардың толық жүйесі. m модулі бойынша қалындылар класы өзінде жататын кезкелген санмен анықталады. Осы класс а+km сандар жиыны болып табылады, яғни а+mZ={a+km  k€Z} немесе amodm={a+km  k€Z}. Қалындылар класына жататын кез келген санды осы кластың өкілі деп атайды. Мысалы: m=2 болса екі қалындылар класы бар: ̅0={…,-4,-2,0,2,4,…}және ̅1={…,-3,-1,3,5,…}.

Анықтама. m модулі бойынша қалындылардың толық жүйесі деп, m модулі бойынша қалындылар кластарының бір-бір өкілінен құрылған m сандар жиынын айтамыз. Мысалы, m=5 үшін: 0,1,2,3,4 – теріс емес кіші қалындылардың толық жүйесі; 1,2,3,4,5 – оң кіші қалындылар жүйесі; -2,-1,0,1,2, - абсолют бойынша кіші қалындылар жүйесі.

---

Смотрите также файлы

• Тесты на курсах сайта sdo sut ru на 60% 1) httpssdo sut rucourseview phpid567 (Английский язык, лексика, семестр 1).docx

• Контрольная работа по теме Личность и общество.docx

• Курляндчик Ирина Владимировна Ф. И. О. учителя Дата проведения 05. 05. 2023 Отметка за конспект.docx

• Отчет по производственной практике (по профилю специальности) по специальности 38. 02. 01 Экономика и бухгалтерский учет (по отраслям).docx

• Аварии на тепловых сетях в холодное время года относятся к.docx