Файл: Лекция Лекция таырыбы Салыстырулар теориясы жне оны арифметикада олданылуы. Жоспары Негізгі тсініктер, салыстыру асиеттері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 124
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тұжырым1. m модулі бойынша екі-екіден салыстырмалы емес m сан қалындылардың толық жүйесін құрайды.
Тұжырым2. а, в бүтін сандар және (а,m)=1 болсын. Егер x1, x2, …, xm сандары m модулі бойынша қалындылардың толық жүйесі болса, онда аx1 +в, аx2 +в, …, аxm+в сандары m модулі бойынша қалындылардың толық жүйесін құрайды.
Қалындылар кластарының жиыны Z/Zm={0modm, 1modm, …(m-1)modm} қосу амалы бойынша аддитивті группа құрайды:
Z/Zm жиынында көбейту амалын да анықтауға болады:
amodm вmodm= aвmodm, 1modm класы көбейту амалы бойынша нейтраль элемент. Демек,
-
Қалындылардың келтірілген жүйесі
n- оң бүтін сан, φ(n) деп n-ге дейінгі n-мен өзара жай сандардың санын белгілейік. Мысалы, n=8 үшін 1,2,3,4,5,6,7 сандарының ішінде 8-бен өзара жай сандардың саны 4, демек φ(8)=4.
(amodm) қалындылар класының барлық санымен m модулінің ЕҮОБ, яғни (а,m) бірдей болады: в € amodm в=mq+a (в,m) =(а,m). Демек, қалындылар класына а элементі тәуелді емес. Егер (а,m)=1 болса, онда (amodm) класы m модулімен өзара жай қалындылар класы деп аталады.
Тұжырым. m модулімен өзара жай қалындылар класының саны φ(m)-ге тең.
Анықтама. m модулі бойынша қалындылардың келтірілген жүйесі деп, осы модуль бойынша өзара жай қалындылар класының әрқайсысынан бір-бірден алынған сандар жиынтығын айтамыз.
Тұжырым1. m>1, m-мен өзара жай және осы модуль бойыншп екі-екіден салыстырымды емес сандар жиынтығы қалындылардың келтірілген жүйесі болады.
Тұжырым2. а€Z және (а,m)=1. Егер в1, в2, …, в φ(m) m модулі бойынша қалындылардың келтірілген жүйесі болса, онда ав1, ав2, …, ав φ(m) m модулі бойынша қалындылардың келтірілген жүйесі болады.
5.Эйлер және Ферма теоремалары
Эйлер функциясы. n-нен аспайтын n-мен өзара жай сандардың санын φ(n) деп белгілейік. Барлық оң сандар жиынында анықталған φ(n) сандық функциясы Эйлер функциясы деп аталады. Мысалы: φ (1)=1; φ(2)=1; φ (6)=2; φ(5)=4;
Теорема.Эйлер функциясы - φ мультипликативті функция.
a>0, b>0 a,b€Z, (a,b)=1, φ(a∙b)= φ(a)∙ φ(b).
Теорема. Егер n=p жай сан болса, онда φ(p)=p-1.
Теорема. Егер n=pk болса, онда φ(pk)=pk-1(p-1).
Теорема. Егер n=
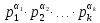болса, онда φ(n)=
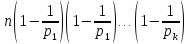.Мысалы: n=288=2532 болса, онда φ(288)=96 ; n=30=2∙3∙5 болса, онда φ(30)=8.
Эйлер функциясының мынадай қасиеті бар: Кез келген p жай және k натурал сандары үшін pk= φ (1)+ φ(p)+ φ(p2)+…+ φ(pk).
Теорема. n санының барлық d натурал бөлгіштері бойынша алынған φ (d) сандарының қосындысы n-ге тең, яғни
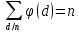
Эйлер теоремасы. Егер а бүтін саны m санымен өзара жай болса, онда aφ (m)≡1(mod m).
Ферма теоремасы. Егер а бүтін саны p жай санына бөлінбесе, онда ap-1≡1(mod p).
Теорема. Егер р-жай сан, а – кезкелген бүтін сан болса, онда ap≡а(mod p).
Эйлер және Ферма теоремаларын пайдаланып санды санға бөлгендегі қалдықты табуға болады. Мысалы. 27 санын 9 санына бөлгендегі қалдықты табыңыз. 26≡1(mod 9). φ (9)=6, 27=26∙2≡1∙2≡2(mod 9).
ax
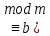) түріндегі бірінші дәрежелі бір айнымалысы бар салыстыруларды шешудің бірнеше әдістерін қарастырайық:-
таңдау әдісі -
коэффициенттерді түрлендіру -
Эйлер әдісі -
Лайықты бөлшектер
Мысалы: 15x
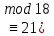) салыстыруды шешейік.Ең алдымен, осы 15x
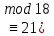) екі жағын 3-ке қысқартып жиберейік. Онда 5x
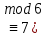) түрге келеді. ЕКОЕ(5,6) =1 болғандықтан есептің тек бір ғана шешімі болады. 1-тәсіл: Таңдау әдісі.
Таңдау әдісі - (
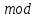m) бойынша толық шегеріндер жүйесіндегі сандарды тексеріп көрейік: {0, 1, 2, 3, 4, 5} (m = 6). Ондаx = 0 болғанда 0
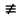7 (mod 6), себебі 0 – 7 = - 7 және ол 6-ға бөлінбейді. Сол сияқты x = 1, 5 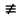7 (mod 6)x = 2, 10
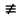7 (mod 6)x = 3, 15
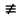7 (mod 6)x = 4, 20
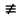7 (mod 6)x = 5, 25
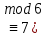), себебі 25 – 7 = 18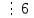 
Осыдан көріп тұрғанымыздай x = 5 берілген салыстыруды қанағаттандырады, себебі x
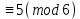.2-тәсіл: Эйлер әдісі
Енді Эйлер формуласын (1) қолдансақ, онда
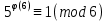тең. 
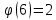болғандықтан, 
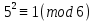шығады. Салыстырудың екі жағын 5-ке көбейтейік: 5*5 x
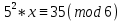
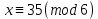
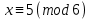
3-тәсіл: Лайықты бөлшектер арқылы
5 x
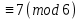
6 :5 = 1,2 және 5:1 = 5 болғандықтан,
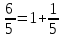= [1; 5], m = 1.| № | 0 | 1 |
| a | 1 | 5 |
| b | 1 | 6 |
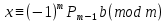формуласын пайдалансақ, онда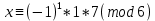 
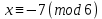
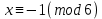
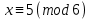
4 – тәсіл. Коэффициенттерді түрлендіру әдісі
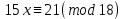салыстырудың екі жағын қысқартып жіберсек, 5x
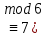) түрге келеді. ЕКОЕ(5,6) = 1 болғандықтан есептің тек бір ғана шешімі болады: 5x
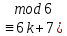), k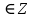
. Осы 6k+7 саны 6-ға бөлінетіндей етіп, k – бүтін санды табайық:
5x
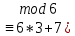) (k = 3 болғанда, 6k+7=6*3+7=25
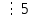)5x
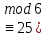)x
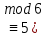)Жауабы: x
)
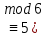