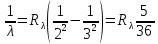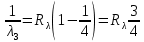Ответ:

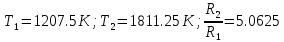
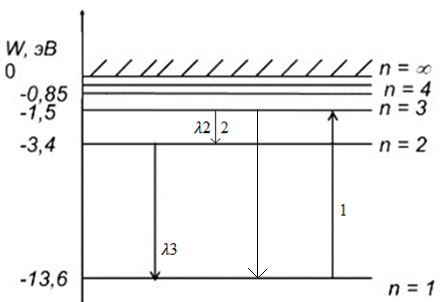
5. Свободный электрон, имея кинетическую энергию 15 эВ, неупруго столкнулся с атомом водорода, находящимся в основном состоянии, и отскочил от него, потеряв часть энергии. Энергия электрона после столкновения оказалась 2.91 эВ. Определить длины волн, которые может излучить атом водорода после столкновения с электроном. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней все переходы между уровнями, которые могут произойти после столкновения.

Дано: T=15 эВ,

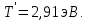
Найти:

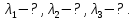
Решение:

Энергия электрона в атоме водорода определяется формулой



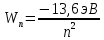
Где

-13,6 эВ – энергия основного состояния,

n – главное квантовое число.

После получения дополнительной энергии 12,09 эВ электрон с основного состояния (h=1) перейдёт в состоянии с «n»:









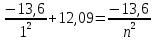
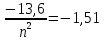
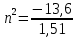
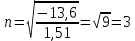
n=3, то электрон перейдёт в состояние с n=3.

По формуле Бора соответствующее излучение имеет длину волны:





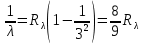
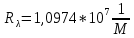
Постоянная Ридберга:



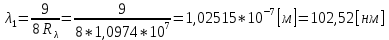
После столкновения может произойти переход:

1. 
   
   

2. 
   
   

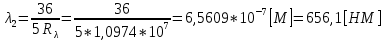
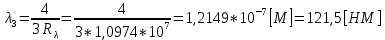
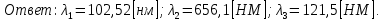
6. При увеличении энергии электрона на 300 эВ его дебройлевская длина волны изменилась в 2 раза. Найти первоначальную длину волны электрона.

---

В этой задаче нет векторных величин.

Длина волны де Бройля определяется по формуле:

λ=hm*v

λ0= 2λ

v=2v0

Ek=m*v22=4m*v022=m*v022+300

m*v022=300эВ3=100 эВ

λ0= hm*v0=h2E kom= 6.62*10-842*300*1.6*10-16*9.1*10-3=6.62*10-8493.5*10-25=0.07*10-9 м

Ответ: : λ0= 0.07*10-9 м.

7. Образец германия с собственной проводимостью при температуре 300 К имеет удельное сопротивление ???? = 0,5 Ом ⋅ м. Подвижность электронов ???????? =0,38 м2 Вс, подвижность дырок ???????? =0,19 м2 Вс, ???? =16. 1. Определить концентрацию собственных носителей заряда. Начертить энергетическую диаграмму, указав положение свободных и связанных электронов, положение дырок. 2. Определить ширину запрещённой зоны Δ????, считая, что в условии задачи плотность состояний в зоне проводимости и в валентной зоне ???????? = ???????? = 2,5 ⋅ 1025м −3 . 3. Найти величину плотности дрейфового тока через образец, если напряжённость поля Е=200 В/м.

Удельная проводимость полупроводника:

σ=e(pi*μp+ni*μn)

e-заряд электрона

p-концентрация дырок

n-концентрация электронов

Удельная проводимость и удельное сопротивление связаны следующей формулой:

σ=1ρ

Так как полупроводник с собственной проводимостью, то

pi=ni

Тогда

σ=eniμp+μn=1ρ

pi=ni=1eρμp+μn=11,6*10-19*0,5*(0,19+0,38)=2,2*1019м-3

Энергетическая диаграмма

Концентрация собственных носителей заряда и плотности состояний связаны следующей формулой:

ni=Nc*Nv*e-ΔW2kT

Прологарифмируем формулу:

ln⁡(ni)=ln⁡(Nc*Nv*e-ΔW2kT)

ln⁡(ni)=ln⁡(Nc*Nv+ln⁡(e-ΔW2kT)

ln⁡(ni)=ln⁡(Nc*Nv)-ΔW2kT

ΔW2kT= ln⁡(Nc*Nv-ln⁡(ni)

ΔW2kT=lnNc*Nvni

ΔW=2kT*lnNc*Nvni

k-постоянная Больцмана

ΔW=2*1,38*10-23*300*ln2,5*1025*2,5*10252,2*1019=1,15*10-19 Дж

Удельная проводимость и плотность дрейфового тока связаны следующей формулой:

σ=JдрE

Jдр= σ*E=1ρ*E=Eρ=2000,5=1000 Aм2

Ответ:

pi=ni=2,2*1019м-3

ΔW=1,15*10-19 Дж

Jдр=1000 Aм2

---

Смотрите также файлы

• Жргізуші Армысыздар, рметті стаздар жне адірменді білім алушылар! Бгінгі Туелсіздігімізді 31 жылдыына арналан Туелсіздік азаттыым, ба кнім! атты мерекелік тарихидеби кешімізге ош келдііздер! Жргізуші1.docx

• ауіпсіздік ережесімен танысу туралы олы.docx

• Общественногосударственная подготовка.doc

• Практическая работа 3 по дисциплине Охрана труда и промышленная безопасность.docx

• Формы объективного права. Текстуальные источники права Корректно ли называть конституцию основным законом.pdf