ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 79
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
 Федеральное государственное бюджетное образовательное учреждение высшего образования
Федеральное государственное бюджетное образовательное учреждение высшего образования«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физике
Расчетно-графическая работа
По дисциплине: Физика
Тема: Электромагнетизм
Вариант №14
Выполнил: ст. группы ИТУ-22-1 /Рыльцев Е.Д./
(должность) (подпись) (Ф.И.О)
ОЦЕНКА: _________
Дата: _____________
Проверил: доцент / Силиванов М.О/
(должность) (подпись) (Ф.И.О)
-
Формулировка задания в соответствии с вариантом
Электрон после прохождения ускоряющей разности потенциалов
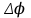 , влетел в расположенный горизонтально плоский конденсатор. Вектор начальной скорости частицы
, влетел в расположенный горизонтально плоский конденсатор. Вектор начальной скорости частицы 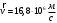 направлен под углом
направлен под углом 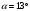 к горизонтальному направлению (см. рис.). Точка влета частицы расположена на расстоянии
к горизонтальному направлению (см. рис.). Точка влета частицы расположена на расстоянии 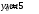 по отношению к нижней пластине конденсатора.
по отношению к нижней пластине конденсатора. К пластинам конденсатора приложено напряжение
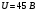 . Расстояние между пластинами ‑
. Расстояние между пластинами ‑ 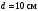 ; длина пластин конденсатора ‑
; длина пластин конденсатора ‑ 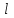 (пластины имеют форму квадрата); С = 35 пФ– электрическая емкость; Q – заряд на обкладках конденсатора1.
(пластины имеют форму квадрата); С = 35 пФ– электрическая емкость; Q – заряд на обкладках конденсатора1.После того как частица покинула конденсатор, она влетела в однородное магнитное поле с магнитной индукцией B= 1,8 Тл, расположенное под углом
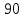 º к плоскости пластин конденсатора и направленное вниз.
º к плоскости пластин конденсатора и направленное вниз.Определить:
-
ускоряющую разность потенциалов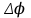 ;
; -
длину пластин конденсатора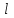 ;
; -
заряд конденсатора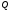 ;
; -
напряжённость электрического поля конденсатора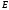 ;
; -
радиус кривизны траектории частицы R; -
шаг траектории частицы в магнитном поле h.
Построить графики зависимости:
-
an(у) – зависимость нормального ускорения частицы от координаты у; -
R(t) – зависимость радиуса кривизны траектории частицы в магнитном поле от времени.
-
Теоретические основы работы:
Явление, изучаемое в РГР –
движение заряженной частицы в электрическом и магнитном поле
Определение основных физических понятий, объектов, процессов и величин:
Энергия - общая количественная мера движения и взаимодействия всех видов материи
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек.
Электрон — стабильная, отрицательно заряженная элементарная частица, одна из основных структурных единиц вещества. Заряд электрона неделим и равен
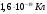 .
.Конденсатор — двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
Также величина ёмкости определяется геометрией конденсатора, а также диэлектрическими свойствами среды, заполняющей пространство между обкладками.
Система отсчета – это совокупность тела отсчета, системы координат и системы отсчета времени, связанных с этим телом, по отношению которого изучается движение (или равновесия) каких-либо других материальных точек или тел.
Координата – это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве.
Законы, используемые при решении поставленных задач:
Второй закон Ньютона: в инерциальных системах ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его равнодействующей сил, совпадает с ней по направлению и обратно пропорционально массе материальной точки:
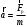 .
.Закон сохранения полной механической энергии: сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной:
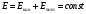 .
.Основные расчётные формулы
Кинетическая энергия частицы:
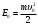
Частица, влетающая в конденсатор параллельно его обкладкам, движется равноускоренно. Уравнения, описывающие движение частицы, имеют вид:
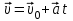 ;
;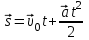 .
.Ёмкость конденсатора:
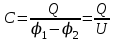 ,
,где
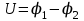 – напряжение (разность потенциалов) между обкладками.
– напряжение (разность потенциалов) между обкладками.Ёмкость плоского конденсатора равна:
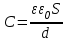 .
.Радиус кривизны траектории:
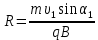 .
.Шаг спирали:
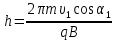 .
.-
Решение задач РГР:
| Дано: 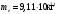 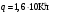 ν = 1,68·107 м/с 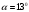 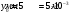 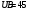 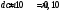 ; ;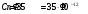 ; ;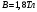 . . |
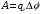 . . Работа сил электрического поля равна в данном случае кинетической энергии Ек , приобретаемой электроном в ускоряющем электрическом поле: 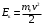 где mе – масса электрона; ν - скорость электрона, с которой он влетает в конденсатор. Приравнивая правые части равенств, получим 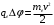 откуда искомая разность потенциалов: |
| Найти:
Построить: R(t), an(t)-? |
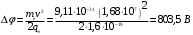
При расчетах заряд электрона берется по модулю, поскольку силы электрического поля совершают положительную работу по перемещению электрона.
.Проверка размерности:
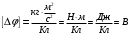
-
Найдём длину пластин конденсатора , применив формулу ёмкости плоского конденсатора:
, применив формулу ёмкости плоского конденсатора:
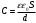 ,
,где
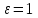 – диэлектрическая проницаемость вакуума;
– диэлектрическая проницаемость вакуума; 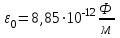 – электрическая постоянная;
– электрическая постоянная;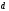 - расстояние между пластинами, S – площадь пластины. Для квадратных пластин с длиной стороны ℓ:
- расстояние между пластинами, S – площадь пластины. Для квадратных пластин с длиной стороны ℓ: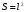
Тогда
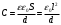
откуда находим:
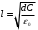
Проверка размерности:
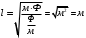
Вычислим:
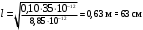
-
Определим заряд конденсатора Q. По определению, электрическая ёмкость С конденсатора – это физическая величина, пропорциональная заряду Q и обратно пропорциональная разности потенциалов U между обкладками :
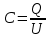
откуда получаем:
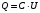 .
.Проверка размерности:
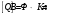 .
.Вычислим:
Q = 35·10-12·45 = 1,58·10-9 Кл = 1,58 нКл
4. Определим напряженность Е электрического поля в конденсаторе. Поскольку в конденсаторе существует однородное электрическое поле, то воспользуемся формулой связи разности потенциалов с напряженностью для однородного поля:
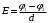 ,
,где d – расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2. Примем расстояние d равным расстоянию между пластинами конденсатора, тогда разность потенциалов (φ1 - φ2) будет равна напряжению U на конденсаторе. Следовательно:
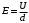
Вычислим:
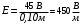
-
Исследуем движение электрона в однородном электрическом поле конденсатора. Электрон в конденсаторе движется под действием электрической силы. Сила тяжести электрона оказывается на много порядков меньше электрической силы, поэтому ею можно пренебречь.
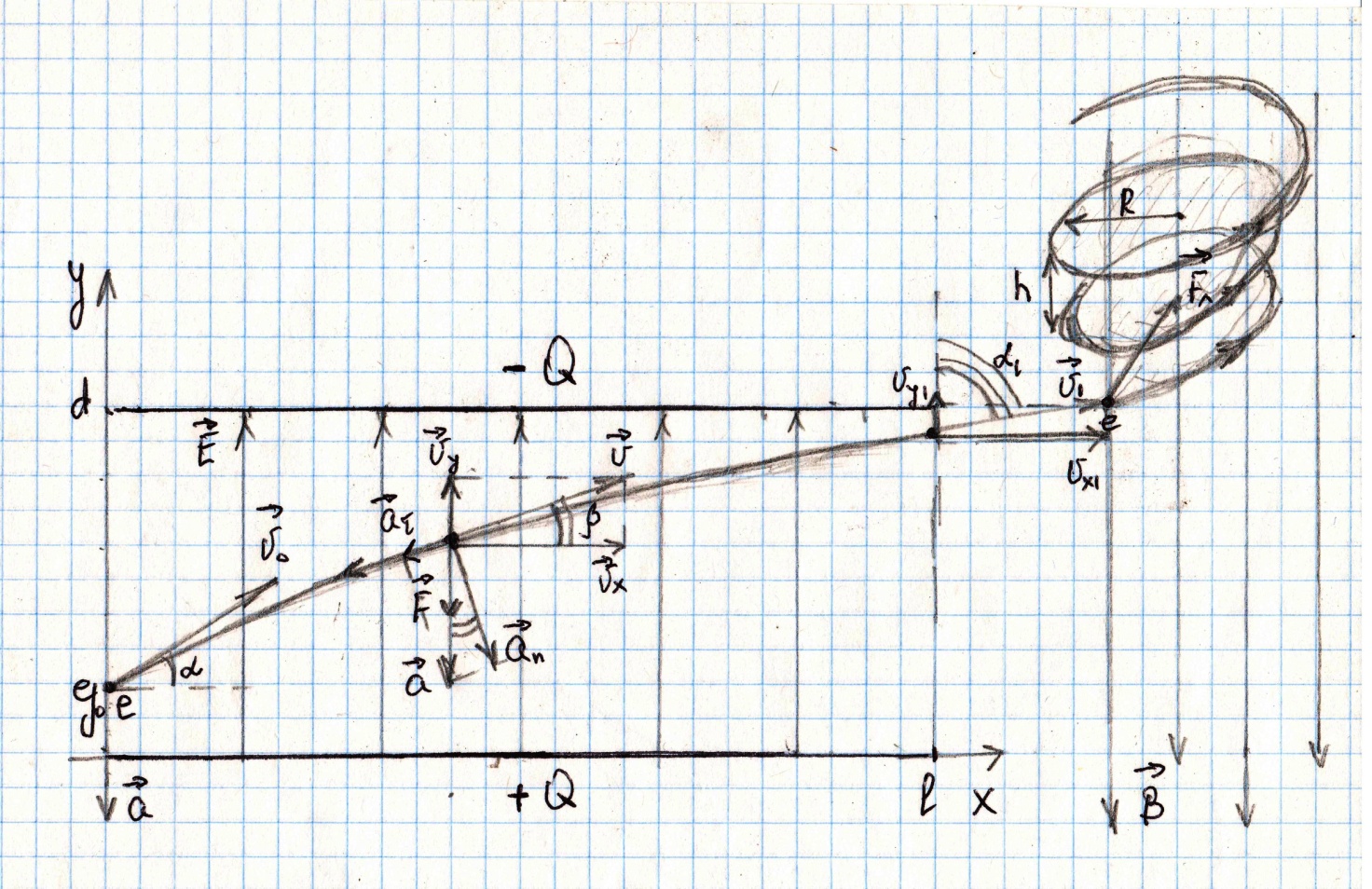
Рис.1.Движение электрона в однородных электрических и магнитных полях
Как указывалось в п. 4 решения, напряженность однородного электрического поля в конденсаторе
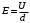 ,
, где U – напряжение между пластинами; d – расстояние между пластинами. Тогда электрическая сила, действующая на электрон в вертикальном направлении,
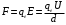 .
. Согласно второму закону Ньютона, под действием этой силы электрон будет двигаться равноускоренно с ускорением
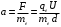 (1)
(1) Уравнение этого движения и уравнение скорости в проекции на оси координат имеют вид:
на ось Ох:
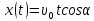 ; (2)
; (2)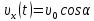 (3)
(3)на ось Оу:
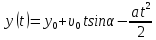 (4)
(4)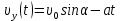 (5)
(5)Когда координата у электрона принимает максимальное значение умах, проекция скорости νу обращается в нуль. Тогда на основании (5):
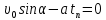
откуда найдем время наивысшего подъема:
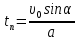
и с учетом (1):
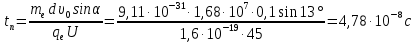
В момент, когда электрон вылетает из конденсатора, его координата х становится равна длине пластины ℓ:
х = ℓ
и с учетом (2):
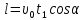
откуда найдем полное время движения электрона в конденсаторе:
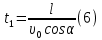
Вычислим:
 -?
-?