Файл: Электромагнетизм.docx

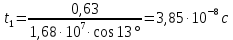
Поскольку t₁ < t_п, то электрон вылетает из конденсатора на восходящей ветви траектории. Его координата у в момент вылета из конденсатора согласно (4):





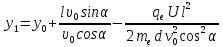
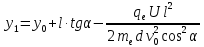
Вычислим:



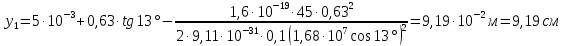
Определим также угол α₁ наклона вектора скорости к вертикали в момент вылета из конденсатора и проекции скорости ν₁ на координатные оси

На основании (5) и (6) получим:



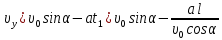
и с учетом (1) окончательно имеем:



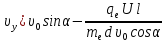
На основании (3):



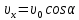
и, как видно из рисунка:




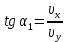
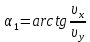
Вычислим:







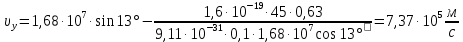
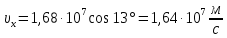
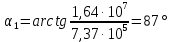
Получим формулу зависимости нормального ускорения электрона а_n от его координаты у. Для этого рассмотрим положение электрона в произвольной точке траектории, где он имеет скорость ν, которая образует с проекцией скорости ν_х угол β. Вектор ускорения 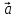в этой точке разложим на нормальную составляющую 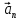и тангенциальную составляющую 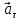Из рисунка видно, что соотношение между составляющими скорости и ускорения частицы выражается формулами:

;

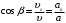откуда:

,

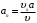где полная скорость частицы:

.

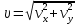Перемещение электрона в вертикальном направлении:

---

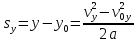
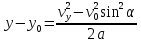
откуда находим:



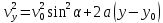
Тогда с учетом формулы (3) скорость электрона в произвольной точке с координатой у равна:





,

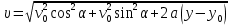
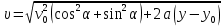
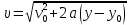а нормальное ускорение электрона зависит от координаты у согласно формуле:



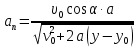
или с учетом формулы (1):

5. 
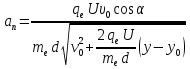
   Таким образом, в магнитное поле электрон влетает под углом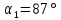 к его силовым линиям, имея составляющую скорости 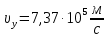, параллельную силовым линиям, и составляющую 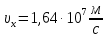, перпендикулярную силовым линиям. Поскольку поле является однородным, то далее под воздействием силы Лоренца частица будет двигаться по винтовой линии с постоянным шагом и радиусом кривизны, сохраняя неизменными свои составляющие скорости. При этом радиус кривизны траектории R зависит от составляющей скорости 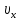, перпендикулярной силовым линиям:
   

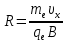
а шаг винтовой линии - от составляющей скорости 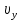, параллельной силовым линиям: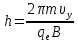



Вычислим:




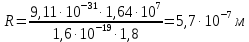
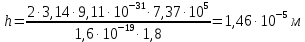
Графический материал:

1. 
   Построим график зависимости радиуса кривизны R траектории частицы в магнитном поле от времени t. Так как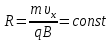 , то можно сделать вывод, что радиус кривизны не зависит от времени движения в однородном магнитном поле. Потому графиком R(t) будет прямая линия, проходящая параллельно оси времени. уравнение которой:
   

---

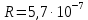
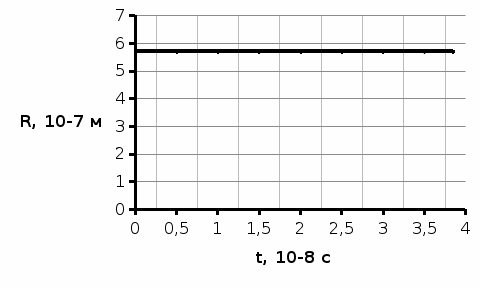
Рис2. График зависимости радиуса кривизны R траектории частицы в магнитном поле от времени t

2. 
   Построим график зависимости нормального ускорения а_n электрона координаты у при его движении в электрическом поле конденсатора. Как было показано выше, уравнение этой зависимости имеет вид:
   

Запишем его с числовыми коэффициентами:

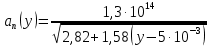
Заполним таблицу значений в пределах 5·10^-3 ≤ у ≤ 92·10^-3 (м)


Таблица значений для построения графика

у, 10-3 м	аn, 1013 м/с2
5	7,74
10	7,73
15	7,72
20	7,71
25	7,7
30	7,69
35	7,68
40	7,67
45	7,66
50	7,65
55	7,64
60	7,62
65	7,61
70	7,6
75	7,59
80	7,58
85	7,57
90	7,56
92	7,56

Рис.3 . График зависимости нормального ускорения а_n электрона координаты у при его движении в электрическом поле конденсатора

Вывод

В расчетно-графическом задании рассматривалось движение электрона в однородном электрическом поле между обкладками заряженного конденсатора, а также в однородном магнитном поле.

В процессе выполнения работы рассчитали необходимые по заданию параметры частицы и конденсатора:

1. 
   ускоряющую разность потенциалов Δφ = 803,5 В;
   
2. 
   длину пластин конденсатора ℓ = 36 см ;
   
3. 
   заряд конденсатора Q = 1,58 нКл;
   
4. 
   напряжённость электрического поля конденсатора = 450 В/м;
   
5. 
   радиус кривизны траектории частицы R = 5,7·10^-7 м;
   
6. 
   шаг траектории частицы в магнитном поле h = 1,46·10^-5 м.
   

---

Построили графики зависимости:

1. 
   a_n(у) – зависимость нормального ускорения частицы от координаты у;
   
2. 
   R(t) – зависимость радиуса кривизны траектории частицы в магнитном поле от времени.
   

---